2025年广西中考数学试题及答案

2025年广西中考数学试题及答案

　　一、单项选择题（本大题共12小题，每小题3分，共36分．在每小题列出的四个备选项中，只有一项符合题目要求，错选、多选或未选均不得分．）

　　1．5的相反数是（   ）

　　A．-5B．0C．1D．5

　　2．在第30个全国“爱眼日”来临之际，某校组织各班围绕“关注普遍的眼健康”开展了手抄报评比，其中九年级6个班得分为：8，9，7，9，10，9，则这组数据的众数为（   ）

　　A．7B．8C．9D．10

　　3．如图是一个正三棱柱，则它的俯视图是（   ）

　　A．B．C．D．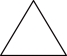

　　4．2025年5月4日，平陆运河青年枢纽电站顺利完成并网调试，具备发电条件．该电站设计年发电量1300万千瓦时，年减排二氧化碳1.17万吨．数据13000000用科学记数法表示为（   ）

　　A．B．C．D．

　　5．有两个容量足够大的玻璃杯，分别装有a克水、b克水，，都加入c克水后，下列式子能反映此时两个玻璃杯中水质量的大小关系的是（   ）

　　A．B．C．D．

　　6．在中，，则（   ）

　　A．B．C．D．

　　7．已知一次函数的图象经过点，则（   ）

　　A．3B．4C．6D．7

　　8．在跳远比赛中，某同学从点C处起跳后，在沙池留下的脚印如图所示，测量线段的长度作为他此次跳远成绩（最近着地点到起跳线的最短距离），依据的数学原理是（   ）

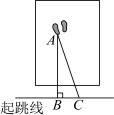
　　A．垂线段最短B．两点确定一条直线

　　C．两点之间，线段最短D．两直线平行，内错角相等

　　9．生态学家G.F.Gause通过多次单独培养大草履虫实验，研究其种群数量随时间的变化情况，得到了如图所示的“S”形曲线．下列说法正确的是（   ）

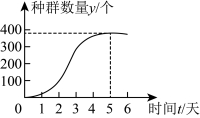
　　A．第5天的种群数量为300个B．前3天种群数量持续增长

　　C．第3天的种群数量达到最大D．每天增加的种群数量相同

　　10．因式分解：（   ）

　　A．B．C．D．

　　11．已知是方程的两个实数根，则（   ）

　　A．B．C．20D．25

　　12．如图，在平面直角坐标系中，“双曲线阶梯”的所有线段均与轴平行或垂直，且满足，点，，，均在双曲线的一支上．若点A的坐标为，则第三级阶梯的高（   ）

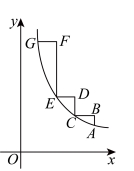
　　A．B．C．D．

　　二、填空题（本大题共4小题，每小题3分，共12分．）

　　13．       ．

　　14．写出一个使分式有意义的的值，可以是      ．

　　15．从三个数字中任选两个，则选出的两个数字之和是偶数的概率为      ．

　　16．如图，点在同侧，，则         ．

　　三、解答题（本大题共7小题，共72分．解答应写出文字说明、证明过程或演算步骤．）

　　17．（）计算：    

　　（）化简：

　　18．绣球是广西民族文化的特色载体．如图，设计某种绣球叶瓣时，可以先在图纸上建立平面直角坐标系，再分别以原点，为圆心、以为半径作圆，两圆相交于两点，其公共部分构成叶瓣①（阴影部分），同理得到叶瓣②．

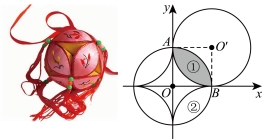
　　(1)写出两点的坐标；

　　(2)求叶瓣①的周长；（结果保留）

　　(3)请描述叶瓣②还可以由叶瓣①经过怎样的图形变化得到．

　　19．某班需从甲、乙两名同学中推荐一人参加校史馆讲解员的选拔，班委决定从口头表达能力、思维能力、表现力、仪容仪表四项内容进行考查．全班同学投票确定了各项所占的百分比，结果如图，再对甲、乙进行考查并逐项打分，成绩如图．

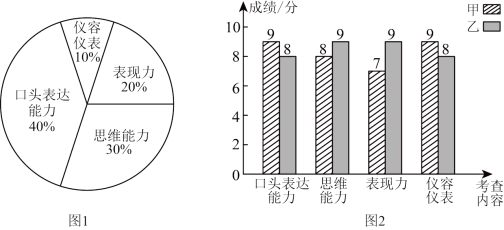
　　(1)在所考查的四项内容中，甲比乙更具优势的有哪些？

　　(2)按照图的各项占比计算甲、乙的综合成绩，并确定推荐人选．

　　20．如图，已知是的直径，点在上，．

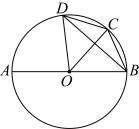
　　(1)求证：；

　　(2)求的度数．

　　21．自2025年5月9日起至2025年12月31日，周末自驾游广西的外省籍小客车，可享受高速公路车辆通行费（以下简称高速费）优惠．小悦一家5月中旬从湖南自驾到广西探亲游玩，此次全程所产生的高速费享受的优惠如下：

　　(1)周六小悦一家从湖南Z市到广西A市，所经湖南境内路段、广西境内特定路段和其他路段的高速费原价分别为a元、b元和c元．求此行程的高速费实付多少元？

　　(2)周日他们从A市到K市（全程在广西境内），高速费实付27.55元；周一从K市原路返回到A市，高速费实付95.95元．求此行程中A市与K市间广西境内特定路段和其他路段的单程高速费原价分别是多少元

　　22．综合与实践

　　树人中学组织一次“爱心义卖”活动．九（5）班分配到了一块矩形义卖区和一把遮阳伞，遮阳伞在地面上的投影是一个平行四边形（如图1）

　　初始时，矩形义卖区与遮阳伞投影的平面图如图2所示，在上，，，，，，由于场地限制，参加义卖的同学只能左右平移遮阳伞．在移动过程中，也随之移动（始终在边所在直线上），且形状大小保持不变，但落在义卖区内的部分（遮阳区）会呈现不同的形状．如图3为移动到落在上的情形．

　　【问题提出】

　　西西同学打算用数学方法，确定遮阳区面积最大时的位置．

　　设遮阳区的面积为，从初始时向右移动的距离为．

　　【直观感知】（1）从初始起右移至图3情形的过程中，随的增大如何变化？

　　【初步探究】（2）求图3情形的与的值；

　　【深入研究】（3）从图3情形起右移至与重合，求该过程中关于的解析式；

　　【问题解决】（4）当遮阳区面积最大时，向右移动了多少？（直接写出结果）

　　23．【平行六边形】如图1，在凸六边形中，满足，我们称这样的凸六边形叫做“平行六边形”，其中与，与，与叫做“主对边”；和，和，和叫做“主对角”；叫做“主对角线”．

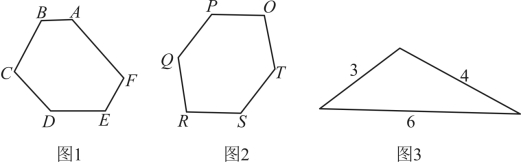
　　(1)类比平行四边形性质，有如下猜想，请判断正误并在横线上填写“正确”或“错误”．

　　【菱六边形】六条边都相等的平行六边形叫做“菱六边形”．

　　(2)如图2，已知平行六边形满足． 求证：平行六边形是菱六边形：

　　(3)如图3是一张边长为的三角形纸片．剪裁掉三个小三角形，使剪裁后的纸片为菱六边形．请在剪裁掉的小三角形中，任选一个，求它的各边长

参考答案

　　1．A

　　2．C

　　3．D

　　4．C

　　5．A

　　6．B

　　7．D

　　8．A

　　9．B

　　10．A

　　11．C

　　12．B

　　13．

　　14．（答案不唯一）

　　15．

　　16．##

　　17．（）；（）

　　18．(1)

　　(2)

　　(3)叶瓣②还可以由叶瓣①逆时针旋转得到

　　19．(1)口头表达能力和仪容仪表

　　(2)推荐乙同学参加

　　20．(1)详见解析

　　(2)

　　【详解】（1）证明：的半径为，

　　，

　　，，

　　；

　　21．

　　(1)

　　(2)特定路段和其他路段的单程高速费原价分别是元和元

　　22．（1）随的增大而增大；（2），；（3）；（4）

　　23．

　　(1)错误；正确；错误

　　(2)详见解析

　　(3)

　　【详解】

　　（2）证明：过点作平行且相等于，连接，

　　则平行四边形是平行四边形，

　　平行于，，

　　在平行六边形中，平行于，，

　　平行且相等于，

　　为平行四边形，

　　平行于，，

　　在平行六边形中，平行于，平行于，

　　平行于，平行于，

　　为平行四边形，

　　，

　　，

　　，

　　，

　　平行六边形是菱六边形．