2025年河北中考数学试题及答案
一、选择题(本大题共12小题,每小题3分,共36分.)
1.从-5℃上升了5℃后的温度,在温度计上显示正确的是( )
A. B.
B. C.
C. D.
D.
2.榫卯结构是两个构件采取凹凸结合的连接方式.如图是某个构件的截面图,其中![]() ,
,![]() ,则
,则![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.计算:![]() ( )
( )
A.2B.4C.6D.8
4.“这么近,那么美,周末到河北”.嘉嘉周末到弘济桥游览,发现青石桥面上有三叶虫化石,他想了解其长度,在化石旁放了一支笔拍下照片(如图).回家后量出照片上笔和化石的长度分别为![]() 和
和![]() ,笔的实际长度为
,笔的实际长度为![]() ,则该化石的实际长度为( )
,则该化石的实际长度为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.一个几何体由圆柱和正方体组成,其主视图、俯视图如图所示,则其左主视图视图为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.若一元二次方程![]() 的两根之和与两根之积分别为
的两根之和与两根之积分别为![]() ,
,![]() ,则点
,则点![]() 在平面直角坐标系中位于( )
在平面直角坐标系中位于( )
A.第一象限B.第二象限C.第三象限D.第四象限
7.抛掷一个质地均匀的正方体木块(6个面上分别标有![]() ,
,![]() ,
,![]() 中的一个数字),若向上一面出现数字1的概率为
中的一个数字),若向上一面出现数字1的概率为![]() ,出现数字2的概率为
,出现数字2的概率为![]() ,则该木块不可能是( )
,则该木块不可能是( )
A. B.
B.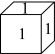 C.
C. D.
D.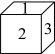
8.若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.3D.6
C.3D.6
9.如图,在五边形![]() 中,
中,![]() ,延长
,延长![]() ,
,![]() ,分别交直线
,分别交直线![]() 于点
于点![]() ,
,![]() .若添加下列一个条件后,仍无法判定
.若添加下列一个条件后,仍无法判定![]() ,则这个条件是( )
,则这个条件是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在反比例函数![]() 中,若
中,若![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.如图,将矩形![]() 沿对角线
沿对角线![]() 折叠,点
折叠,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() .将
.将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在
落在![]() 内的
内的![]() 处,下列结论一定正确的是( )
处,下列结论一定正确的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.在平面直角坐标系中,横、纵坐标都是整数的点称为整点.如图,正方形![]() 与正方形
与正方形![]() 的顶点均为整点.若只将正方形
的顶点均为整点.若只将正方形![]() 平移,使其内部(不含边界)有且只有
平移,使其内部(不含边界)有且只有![]() ,
,![]() ,
,![]() 三个整点,则平移后点
三个整点,则平移后点![]() 的对应点坐标为( )
的对应点坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共4小题,每小题3分,共12分)
13.计算:![]() .
.
14.平行四边形的一组邻边长分别为![]() ,
,![]() ,一条对角线长为
,一条对角线长为![]() .若
.若![]() 为整数,则
为整数,则![]() 的值可以为 .(写出一个即可)
的值可以为 .(写出一个即可)
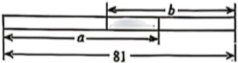
15.甲、乙两张等宽的长方形纸条,长分别为![]() ,
,![]() .如图,将甲纸条的
.如图,将甲纸条的![]() 与乙纸条的
与乙纸条的![]() 叠合在一起,形成长为81的纸条,则
叠合在一起,形成长为81的纸条,则![]() .
.
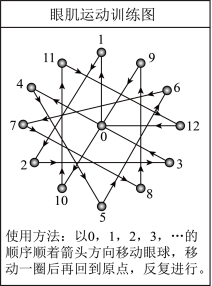
16.2025年3月是第10个全国近视防控宣传教育月,活动主题为“抓早抓小抓关键,更快降低近视率”,图是一幅眼肌运动训练图,其中数字![]() 对应的点均匀分布在一个圆上,数字0对应圆心.图中以数字
对应的点均匀分布在一个圆上,数字0对应圆心.图中以数字![]() 对应的点为端点的所有线段中,有一条线段的长与其他的都不相等.若该圆的半径为1,则这条线段的长为 .(参考数据:
对应的点为端点的所有线段中,有一条线段的长与其他的都不相等.若该圆的半径为1,则这条线段的长为 .(参考数据:![]() ,
,![]() )
)
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤).
17.(1)解不等式![]() ,并在如图所给的数轴上表示其解集;
,并在如图所给的数轴上表示其解集;
(2)解不等式![]() ,并在如图所给的数轴上表示其解集;
,并在如图所给的数轴上表示其解集;
(3)直接写出不等式组![]() 的解集.
的解集.
![]()
18.(1)一道习题及其错误的解答过程如下:请指出在第几步开始出现错误,并选择你喜欢的方法写出正确的解答过程.
计算: 解: |
(2)计算:![]()
19.如图.四边形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() .
.
20.某工厂生产![]() ,
,![]() ,
,![]() ,
,![]() 四种产品.为提升产品的竞争力,该工厂计划对部分种类的产品优化生产流程,降低成本;对其他种类的产品增加研发投入,提升品质.经研究,该工厂做出了甲、乙两种调整方案,这两种方案将对四种产品的成本产生不同的影响.下面是该工厂这四种产品的部分信息:a.调整前,各产品年产量的不完整的条形统计图(图1)和扇形统计图(图2).b.各产品单件成本的核算情况统计表及说明.说明:对于统计表中的数据,方案甲的平均数与调整前的相同,方案乙的中位数与调整前的相同.根据以上信息,解答下列问题:
四种产品.为提升产品的竞争力,该工厂计划对部分种类的产品优化生产流程,降低成本;对其他种类的产品增加研发投入,提升品质.经研究,该工厂做出了甲、乙两种调整方案,这两种方案将对四种产品的成本产生不同的影响.下面是该工厂这四种产品的部分信息:a.调整前,各产品年产量的不完整的条形统计图(图1)和扇形统计图(图2).b.各产品单件成本的核算情况统计表及说明.说明:对于统计表中的数据,方案甲的平均数与调整前的相同,方案乙的中位数与调整前的相同.根据以上信息,解答下列问题:

产品数据 类别 | | | | | |
调整前单价成本(元/件) | | | | | |
调整后单价成本(元/件) | 方案甲 | | | | |
方案乙 | | | | | |
(1)求调整前![]() 产品的年产量;
产品的年产量;
(2)直接写出![]() ,
,![]() 的值;
的值;
(3)若调整后这四种产品的年产量均与调整前的相同,请通过计算说明甲、乙两种方案哪种总成本较低
21.如图1,图2,正方形![]() 的边长为5.扇形
的边长为5.扇形![]() 所在圆的圆心
所在圆的圆心![]() 在对角线
在对角线![]() 上,且不与点
上,且不与点![]() 重合,半径
重合,半径![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]()
![]() ,扇形
,扇形![]() 的弧交线段
的弧交线段![]() 于点
于点![]() ,记为
,记为![]() .
.

(1)如图1,当![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图2,当四边形![]() 为菱形时,求
为菱形时,求![]() 的长;
的长;
(3)当![]() 时,求
时,求![]() 的长.
的长.
22.一般固体都具有热胀冷缩的性质,固体受热后其长度的增加称为线膨胀.在![]() (本题涉及的温度均在此范围内),原长为
(本题涉及的温度均在此范围内),原长为![]() 的铜棒、铁棒受热后,伸长量
的铜棒、铁棒受热后,伸长量![]() 与温度的增加量
与温度的增加量![]() 之间的关系均为
之间的关系均为![]() ,其中
,其中![]() 为常数,称为该金属的线膨胀系数.已知铜的线膨胀系数
为常数,称为该金属的线膨胀系数.已知铜的线膨胀系数![]() (单位:
(单位:![]() );原长为
);原长为![]() 的铁棒从
的铁棒从![]() 加热到
加热到![]() 伸长了
伸长了![]() .
.
(1)原长为![]() 的铜棒受热后升高
的铜棒受热后升高![]() ,求该铜棒的伸长量(用科学记数法表示).
,求该铜棒的伸长量(用科学记数法表示).
(2)求铁的线膨胀系数![]() ;若原长为
;若原长为![]() 的铁棒受热后伸长
的铁棒受热后伸长![]() ,求该铁棒温度的增加量.
,求该铁棒温度的增加量.
(3)将原长相等的铜棒和铁棒从![]() 开始分别加热,当它们的伸长量相同时,若铁棒的温度比铜棒的高
开始分别加热,当它们的伸长量相同时,若铁棒的温度比铜棒的高![]() ,求该铁棒温度的增加量.
,求该铁棒温度的增加量.
23.综合与实践
[情境]要将矩形铁板切割成相同的两部分,焊接成直角护板(如图![]() ),需找到合适的切割线.
),需找到合适的切割线.
[模型]已知矩形![]() (数据如图
(数据如图![]() 所示).作一条直线
所示).作一条直线![]() ,使
,使![]() 与
与![]() 所夹的锐角为
所夹的锐角为![]() ,且将矩形
,且将矩形![]() 分成周长相等的两部分.
分成周长相等的两部分.
[操作]嘉嘉和淇淇尝试用不同方法解决问题.
[探究]根据以上描述,解决下列问题
[拓展]操作和探究中蕴含着一般性结论,请继续研究下面的问题.

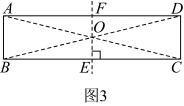
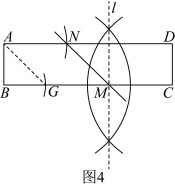
如图3,嘉嘉的思路如下: ①连接 ②过点 …… | 如图4,淇淇的方法如下: ①在边 ②作线段 ③在边 |
(1)图![]() 中,矩形
中,矩形![]() 的周长为______;
的周长为______;
(2)在图![]() 的基础上,用尺规作图作出直线
的基础上,用尺规作图作出直线![]() (作出一条即可,保留作图痕迹,不写作法);
(作出一条即可,保留作图痕迹,不写作法);
(3)根据淇淇的作图过程,请说明图![]() 中的直线
中的直线![]() 符合要求.
符合要求.
(4)如图![]() ,若直线
,若直线![]() 将矩形
将矩形![]() 分成周长相等的两部分,分别交边
分成周长相等的两部分,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 当
当![]() 时,求
时,求![]() 的值;
的值;
![]() 当
当![]() 最大时,直接写出
最大时,直接写出![]() 的长.
的长.
24.如图,在平面直角坐标系中,抛物线![]() 经过点
经过点![]() ,
,![]() ,顶点为
,顶点为![]() .抛物线
.抛物线![]() 经过点
经过点![]() .两条抛物线在第一象限内的部分分别记为
.两条抛物线在第一象限内的部分分别记为![]() ,
,![]() .
.

(1)求![]() ,
,![]() 的值及点
的值及点![]() 的坐标.
的坐标.
(2)点![]() 在
在![]() 上,到
上,到![]() 轴的距离为
轴的距离为![]() .判断
.判断![]() 能否经过点
能否经过点![]() ,若能,求
,若能,求![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
(3)直线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上,且点
上,且点![]() 的横坐标是点
的横坐标是点![]() 横坐标的一半.
横坐标的一半.
①若点![]() 与点
与点![]() 重合,点
重合,点![]() 恰好落在
恰好落在![]() 上,求
上,求![]() 的值;
的值;
②若点![]() 为直线
为直线![]() 与
与![]() 的唯一公共点,请直接写出
的唯一公共点,请直接写出![]() 的值.
的值.
参考答案
1.B
2.C
3.B
4.C
5.A
6.C
7.A
8.B
9.D
10.B
11.D
12.A
13.![]()
14.![]() (答案不唯一)
(答案不唯一)
15.99
16.![]()
17.(1)![]() ,见解析;(2)
,见解析;(2)![]() ,见解析;(3)
,见解析;(3)![]()
18.(1)原计算第一步开始出错;![]() ;(2)
;(2)![]()
19.
【详解】(1)证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ;
;
(2)证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() .
.
20.(1)![]() 万件
万件
(2)![]() ,
,![]()
(3)甲种方案总成本较低
21.(1)![]()
(2)![]()
(3)![]() 或
或![]()
22.(1)![]()
![]()
(2)![]()
![]() ,
,![]()
(3)![]()
23.(1)![]() ;
;
(2)见解析;
(3)![]() ;
;
(4)![]() ;
;![]() .
.
【详解】
(2)解:如下图所示,
以点![]() 为圆心
为圆心![]() 为半径画弧,交
为半径画弧,交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,线段
,线段![]() 即为所求,
即为所求,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() 矩形
矩形![]() 的对角线交于点
的对角线交于点![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,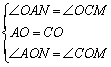 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 把矩形
把矩形![]() 分成周长相等的两部分;
分成周长相等的两部分;

24.(1)![]() ,
,![]()
(2)不能,理由见解析
(3)①![]() ;②
;②![]()
【详解】
(2)∵点![]() 在
在![]() (第一象限)上,到
(第一象限)上,到![]() 轴的距离为
轴的距离为![]() .则
.则![]()
∴当![]() 时,
时,![]()
解得:![]() 或
或![]()
∴![]() 或
或![]()
∵抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]()
∴![]() 经过点
经过点![]() 和
和![]()
∴![]() 不能经过点
不能经过点![]()