2025年陕西中考数学试题及答案
第一部分(选择题,共24分)
一、选择题(共8小题,每小题3分,计24分,每小题只有一个选项是符合题意的)
1.计算:-5+4=( )
A.1B.-1C.9D.-9
2.上马石是古人上下马的工具,形状如图①.它可以看作图②所示的几何体,该几何体的俯视图为( )

A.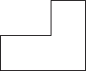 B.
B.![]() C.
C.![]() D.
D.![]()
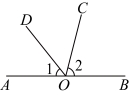
3.如图,点![]() 在直线
在直线![]() 上,
上,![]() 平分
平分![]() .若
.若![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.计算![]() 的结果为( )
的结果为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
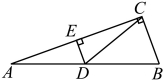
5.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的中线,
边上的中线,![]() ,则图中与
,则图中与![]() 互余的角共有( )
互余的角共有( )
A.2个B.3个C.4个D.5个
6.在平面直角坐标系中,过点![]() ,
,![]() 的直线向上平移3个单位长度,平移后的直线经过的点的坐标可以是( )
的直线向上平移3个单位长度,平移后的直线经过的点的坐标可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如图,正方形![]() 的边长为4,点
的边长为4,点![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() ,则
,则![]() 的面积为( )
的面积为( )
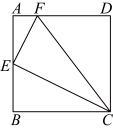
A.10B.8C.5D.4
8.在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴有两个交点,且这两个交点分别位于
轴有两个交点,且这两个交点分别位于![]() 轴两侧,则下列关于该函数的结论正确的是( )
轴两侧,则下列关于该函数的结论正确的是( )
A.图象的开口向下B.当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大
值的增大而增大
C.函数的最小值小于![]() D.当
D.当![]() 时,
时,![]()
二、填空题(共6小题,每小题3分,计18分)
9.满足![]() 的整数
的整数![]() 可以是 (写出一个符合题意的数即可).
可以是 (写出一个符合题意的数即可).
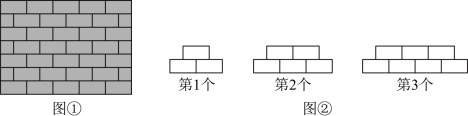
10.生活中常按图①的方式砌墙,小华模仿这样的方式,用全等的矩形按规律设计图案,如图②,第1个图案用了3个矩形,第2个图案用了5个矩形,第3个图案用了7个矩形,……则第10个图案需要用矩形的个数为 .
11.草莓熟了,学校组织同学们参加劳动实践,帮助果农采摘草莓.小康和小悦采摘的时长相同,采摘结束后,小康采摘的草莓比小悦多![]() .已知小康平均每小时采摘
.已知小康平均每小时采摘![]() ,小悦平均每小时采摘
,小悦平均每小时采摘![]() ,小康采摘的时长是 小时.
,小康采摘的时长是 小时.
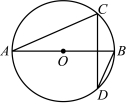
12.如图,![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() ,则
,则![]() 的度数为
的度数为
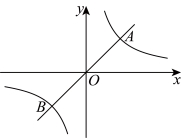
13.如图,过原点的直线与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,则
两点,则![]() 的值为 .
的值为 .
14.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,以
,以![]() 为边作等边
为边作等边![]() ,使点
,使点![]() 始终在
始终在![]() 的内部或边上.当
的内部或边上.当![]() 的面积最大时,
的面积最大时,![]() 的长为 .
的长为 .
三、解答题(共12小题,计78分.解答应写出过程)
15.计算:![]() .
.
16.解不等式组:![]()
17.化简:![]() .
.
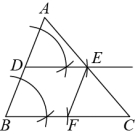
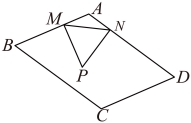
18.如图,已知![]() ,点
,点![]() 在边
在边![]() 上.请用尺规作图法,在
上.请用尺规作图法,在![]() 的内部求作一点
的内部求作一点![]() ,使得
,使得![]() ,且
,且![]() .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)
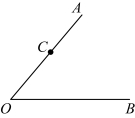
19.如图,点![]() 是
是![]() 的边
的边![]() 延长线上一点,
延长线上一点,![]() ,
,![]() ,
,![]() .求证:
.求证:![]()
20.某班开展主题为“我爱陕西”的综合实践活动,班委会决定设置“山水”“历史”“文学”“艺术”“科技”(分别记作![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )共五个研究方向,并采取小组合作的研究方式.同学们在五张完全相同的不透明卡片的正面绘制了如图所示的图案,卡片背面保持完全相同.
)共五个研究方向,并采取小组合作的研究方式.同学们在五张完全相同的不透明卡片的正面绘制了如图所示的图案,卡片背面保持完全相同.

(1)将这五张卡片背面朝上洗匀后,从中随机抽取一张,抽到的卡片内容是“科技”的概率为______;
(2)各小组从这五张卡片中随机抽取一张,将卡片内容作为本小组的研究方向.将这五张卡片背面朝上洗匀后,小秦代表第一小组从中随机抽取一张,记下结果,放回,背面朝上洗匀后,小博代表第二小组从中随机抽取一张.请用列表或画树状图的方法,求这两个小组研究方向不同的概率.
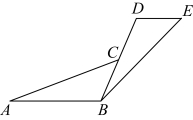
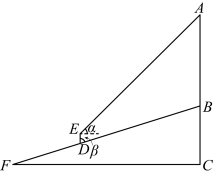
21.小涵和小宇想测量公园山坡上一个信号杆的高度.在征得家长同意后,他们带着工具前往测量.测量示意图如图所示,他们在坡面![]() 上的点
上的点![]() 处安装测角仪
处安装测角仪![]() ,测得信号杆顶端
,测得信号杆顶端![]() 的仰角
的仰角![]() 为
为![]() ,
,![]() 与坡面的夹角
与坡面的夹角![]() 为
为![]() ,又测得点
,又测得点![]() 与信号杆底端
与信号杆底端![]() 之间的距离
之间的距离![]() 为
为![]() .已知
.已知![]() ,点
,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() ,
,![]() 均与水平线
均与水平线![]() 垂直.求信号杆的高
垂直.求信号杆的高![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() )
)
22.研究表明,一定质量的气体,在压强不变的条件下,气体体积![]() 与气体温度
与气体温度![]() 成一次函数关系.某实验室在压强不变的条件下,对一定质量的某种气体进行加热,测得的部分数据如下表:
成一次函数关系.某实验室在压强不变的条件下,对一定质量的某种气体进行加热,测得的部分数据如下表:
气体温度 | … | 25 | 30 | 35 | … |
气体体积 | … | 596 | 606 | 616 | … |
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)为满足下一步的实验需求,本次实验要求气体体积达到![]() 时停止加热.求停止加热时的气体温度.
时停止加热.求停止加热时的气体温度.
23.为了让同学们了解我国航天事业取得的成就并普及航天知识,某校在“中国航天日”当天开展了研学活动,随后采取自愿报名的方式,组织了航天知识竞赛.竞赛结束后,从竞赛成绩(单位:分 满分100分 均不低于60分)中用科学的抽样方法随机抽取部分成绩,并进行整理,绘制了如下统计图:

其中B组共有15个成绩,从高到低分别为:89,88,88,86,85,85,85,85,84,83,81,81,80,80,80.
根据以上信息,解答下列问题:
(1)B组15个成绩的平均数为______分;
(2)本次被抽取的所有成绩的个数为______,本次被抽取的所有成绩的中位数为______分;
(3)学校决定对本次竞赛成绩90分及以上的学生进行奖励,该校共有500名学生参加竞赛,请估计本次竞赛的获奖人数.
24.如图,点![]() 在
在![]() 的边
的边![]() 上,以
上,以![]() 为半径的⊙
为半径的⊙![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]()
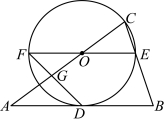
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
25.某景区大门上半部分的截面示意图如图所示,顶部![]() ,左、右门洞
,左、右门洞![]() ,
,![]() 均呈抛物线型,水平横梁
均呈抛物线型,水平横梁![]() ,
,![]() 的最高点
的最高点![]() 到
到![]() 的距离
的距离![]() ,
,![]() ,
,![]() 关于
关于![]() 所在直线对称.
所在直线对称.![]() ,
,![]() ,
,![]() 为框架,点
为框架,点![]() ,
,![]() 在
在![]() 上,点
上,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,
,![]() ,
,![]() .以
.以![]() 为原点,以
为原点,以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系
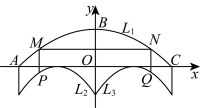
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)已知抛物线![]() 的函数表达式为
的函数表达式为![]() ,
,![]() ,求
,求![]() 的长.
的长.
26.问题探究
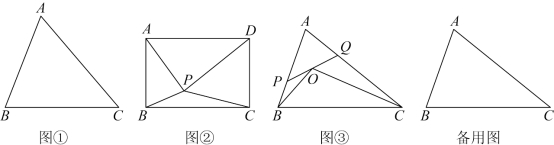
(1)如图①,在![]() 中,请画出一个
中,请画出一个![]() ,使得点
,使得点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上;
上;
(2)如图②,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 内一点,且满足
内一点,且满足![]() ,
,![]() 周长的最小值;
周长的最小值;
问题解决
(3)为了进一步提升游客的体验感,某公园管理部门准备在花海边沿与游客服务中心之间的草地上选址修建一条笔直的步道及一个观景台.如图③所示,![]() 区域为草地,线段
区域为草地,线段![]() 为花海边沿,点
为花海边沿,点![]() 为游客服务中心,线段
为游客服务中心,线段![]() 为步道,点
为步道,点![]() 和点
和点![]() 为步道口,点
为步道口,点![]() 为观景台.按照设计要求,点
为观景台.按照设计要求,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且满足
上,且满足![]() ,
,![]() 为
为![]() 的中点,为保证观赏花海的最佳效果,还需使
的中点,为保证观赏花海的最佳效果,还需使![]() 最大.已知
最大.已知![]() ,
,![]() ,请你帮助公园管理部门确定观景台的位置(在图中画出符合条件的点),并计算此时步道口
,请你帮助公园管理部门确定观景台的位置(在图中画出符合条件的点),并计算此时步道口![]() 与游客服务中心
与游客服务中心![]() 之间的距离
之间的距离![]() .(步道的宽及步道口、观景台、游客服务中心的大小均忽略不计)
.(步道的宽及步道口、观景台、游客服务中心的大小均忽略不计)
参考答案
1.B
2.D
3.A
4.D
5.C
6.B
7.C
8.D
9.3(答案不唯一)
10.21
11.![]()
12.![]()
13.9
14.5
15.7
16.![]()
17.![]()
18.
【详解】解:如图,点![]() 即为所求;
即为所求;
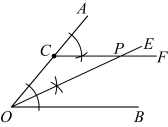
理由如下:
由作图可知:![]() 是
是![]() 的平分线,
的平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点![]() 即为所求
即为所求
19.
【详解】证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
20.(1)![]()
(2)![]()
21.信号杆的高![]() 为
为![]()
22.(1)![]()
(2)![]()
23.
(1)![]()
(2)![]() ,
,![]()
(3)![]() 人
人
24.
(1)证明见解析
(2)![]()
【详解】(1)解:如图,连接![]() ,
,
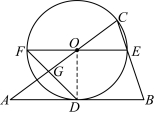
∵以![]() 为半径的⊙
为半径的⊙![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
25.(1)![]()
(2)![]()
26.(1)见详解(2)![]() (3)
(3)![]()
【详解】解:(1)依题意,
先作![]() ,
,![]() 交
交![]() 于点
于点![]() ,得出
,得出![]() ,再以点B为圆心,以
,再以点B为圆心,以![]() 的长为半径画弧,交线段
的长为半径画弧,交线段![]() 于一点
于一点![]() ,连接
,连接![]() ,
,
则![]() ,
,
∵![]()
∴四边形![]() 是平行四边形,
是平行四边形,
即![]() 如图所示:
如图所示: