2025年湖北中考数学试题及答案
一、选择题(共10题,每题3分,共30分.在每题给出的四个选项中,只有一项符合题目要求)
1.数轴上表示数a,b的点如图所示,下列判断正确的是( )
![]()
A.abC.b
2.“月壤砖”是我国科学家模拟月壤成分烧制而成的,拟用于未来建造月球基地.如图是一种“月壤砖”的示意图,它的主视图是( )
A.![]() B.
B.
C. D.
D.![]()
3.下列运算的结果为![]() 的是( )
的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.一元二次方程![]() 的两个实数根为
的两个实数根为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
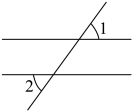
5.数学中的“![]() ”可以看作是两条平行的线段被第三条线段所截而成,放大后如图所示.若
”可以看作是两条平行的线段被第三条线段所截而成,放大后如图所示.若![]() ,则
,则![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在下列事件中,不可能事件是( )
A.投掷一枚硬币,正面向上B.从只有红球的袋子中摸出黄球
C.任意画一个圆,它是轴对称图形D.射击运动员射击一次,命中靶心
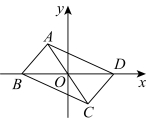
7.如图,平行四边形![]() 的对角线交点在原点.若
的对角线交点在原点.若![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
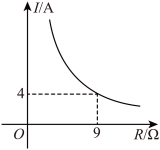
8.已知蓄电池的电压为定值,使用蓄电池时,电流![]() (单位:A)与电阻
(单位:A)与电阻![]() (单位:
(单位:![]() )是反比例函数关系,它的图象如图所示.当电阻
)是反比例函数关系,它的图象如图所示.当电阻![]() 大于
大于![]() 时,电流
时,电流![]() 可能是( )
可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图,![]() 内接于
内接于![]() .分别以点
.分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于M,N两点,作直线
的长为半径作弧,两弧交于M,N两点,作直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 的度数是( )
的度数是( )
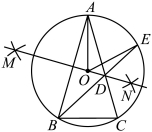
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,折叠正方形![]() 的一边
的一边![]() ,使点
,使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .若
.若![]() ,则
,则![]() 的长是( )
的长是( )
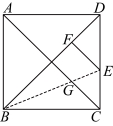
A.![]() B.2C.
B.2C.![]() D.
D.![]()
二、填空题(共5题,每题3分,共15分)
11.一个矩形相邻两边的长分别为2,m,则这个矩形的面积是 .
12.已知一次函数![]() 随
随![]() 的增大而增大.写出一个符合条件的
的增大而增大.写出一个符合条件的![]() 的值是 .
的值是 .
13.窗,让人足不出户便能将室外天地尽收眼底.如图,“步步锦”“龟背锦”“灯笼锦”是我国传统的窗格构造方式,从这三种方式中随机选出一种制作窗格,选中“步步锦”的概率是 .

14.计算![]() 的结果是 .
的结果是 .
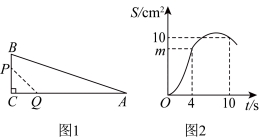
15.如图1,在![]() 中,
中,![]() .动点P,Q均以
.动点P,Q均以![]() 的速度从点
的速度从点![]() 同时出发,点
同时出发,点![]() 沿折线
沿折线![]() 向点
向点![]() 运动,点
运动,点![]() 沿边CA向点
沿边CA向点![]() 运动.当点
运动.当点![]() 运动到点
运动到点![]() 时,两点都停止运动.
时,两点都停止运动.![]() 的面积
的面积![]() (单位:
(单位:![]() )与运动时间
)与运动时间![]() (单位:s)的关系如图2所示.(1)
(单位:s)的关系如图2所示.(1)![]() ;(2)
;(2)![]()
三、解答题(共9题,共75分)
16.计算:![]() .
.
17.如图,![]() 平分
平分![]() .求证:
.求证:![]() .
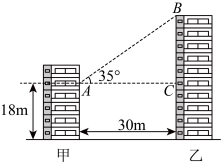
.
18.如图,甲、乙两栋楼相距30m,从甲楼![]() 处看乙楼顶部
处看乙楼顶部![]() 的仰角为
的仰角为![]() 到地面的距离为18m,求乙楼的高.(参考数据:
到地面的距离为18m,求乙楼的高.(参考数据:![]() )
)
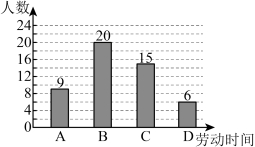
19.为加强劳动教育,学校制定了《劳动习惯养成计划》,实施“家校社”联动行动,引导学生参与家务劳动、公益劳动等实践活动.学校在学期初和学期末分别对七年级学生开展了“一周参与劳动时间”的问卷调查,两次调查均随机抽取50名学生.根据收集到的数据,将劳动时间![]() (单位:
(单位:![]() )分为
)分为![]() ,
,![]() 四组进行统计,并绘制了学期初调查数据条形图,学期末调查数据扇形图和两次调查数据的平均数、中位数、众数统计表,部分信息如下.
四组进行统计,并绘制了学期初调查数据条形图,学期末调查数据扇形图和两次调查数据的平均数、中位数、众数统计表,部分信息如下.
学期初调查数据条形图 学期末调查数据扇形图
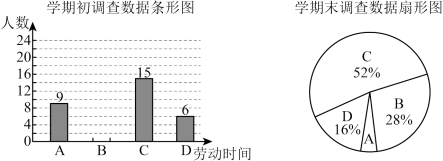
两次调查数据统计表
时间 | 平均数 | 中位数 | 众数 |
学期初 | 2.8 | 2.9 | 2.8 |
学期末 | 3.5 | 3.6 | 3.6 |
(1)在学期初调查数据条形图中,B组人数是______人,并补全条形图;
(2)七年级有500名学生,估计学期末七年级学生一周参与劳动时间不低于![]() 的人数;
的人数;
(3)该校七年级学生一周参与劳动时间,学期末比学期初有没有提高?结合统计数据说明理由.
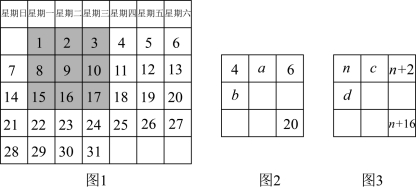
20.幻方起源于中国,月历常用于生活,它们有很多奥秘,探究并完成填空.
主题 | 探究月历与幻方的奥秘 |
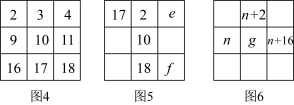
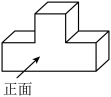
活动一 | 图1是某月的月历,用方框选取了其中的9个数. (1)移动方框,若方框中的部分数如图2所示,则 (2)移动方框,若方框中的部分数如图3所示,则 (注:用含 |
活动二 | 移动方框选取月历中的9个数,调整它们的位置,使其满足“三阶幻方”分布规律:每一横行、每一竖列以及两条斜对角线上的三个数的和都相等. (3)若方框选取的数如图4所示,调整后,部分数的位置如图5所示,则 (4)若方框选取的数中最小的数是 |
21.如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .过点
.过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .
.
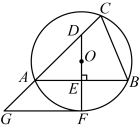
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的半径.
的半径.
22.某商店销售A,B两种水果.A水果标价14元/千克,B水果标价18元/千克.
(1)小明陪妈妈在这家商店按标价买了A,B两种水果共3千克,合计付款46元.这两种水果各买了多少千克?
(2)妈妈让小明再到这家商店买![]() 两种水果,要求B水果比A水果多买1千克,合计付款不超过50元.设小明买A水果
两种水果,要求B水果比A水果多买1千克,合计付款不超过50元.设小明买A水果![]() 千克.
千克.
①若这两种水果按标价出售,求![]() 的取值范围;
的取值范围;
②小明到这家商店后,发现![]() 两种水果正在进行优惠活动:A水果打七五折;一次购买B水果不超过1千克不优惠,超过1千克后,超过1千克的部分打七五折.(注:“打七五折”指按标价的
两种水果正在进行优惠活动:A水果打七五折;一次购买B水果不超过1千克不优惠,超过1千克后,超过1千克的部分打七五折.(注:“打七五折”指按标价的![]() 出售.)若小明合计付款48元,求
出售.)若小明合计付款48元,求![]() 的值.
的值.
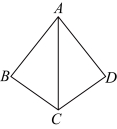
23.在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 旋转得到
旋转得到![]() ,点
,点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,连接
上,连接![]() .
.
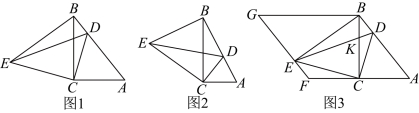
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,求
时,求![]() 的长;
的长;
(3)如图3,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点G,
于点G,![]() 与
与![]() 交于点
交于点![]() .
.
①求证:![]() ;
;
②当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
24.抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() 和点
和点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,
,![]() 是抛物线的顶点,
是抛物线的顶点,![]() 是抛物线上一动点,设点
是抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
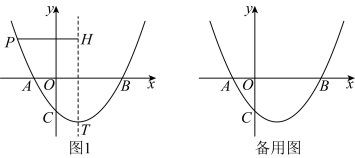
(1)求![]() 的值;
的值;
(2)如图1,若点![]() 在对称轴左侧,过点
在对称轴左侧,过点![]() 作对称轴的垂线,垂足为
作对称轴的垂线,垂足为![]() ,求
,求![]() 的值;
的值;
(3)定义:抛物线上两点M,N之间的部分叫做抛物线弧![]() (含端点
(含端点![]() 和
和![]() ).过
).过![]() ,
,![]() 分别作
分别作![]() 轴的垂线
轴的垂线![]() ,过抛物线弧
,过抛物线弧![]() 的最高点和最低点分别作
的最高点和最低点分别作![]() 轴的垂线
轴的垂线![]() ,直线
,直线![]() 与
与![]() 围成的矩形叫做抛物线弧
围成的矩形叫做抛物线弧![]() 的特征矩形.若点
的特征矩形.若点![]() 在第四象限,记抛物线弧
在第四象限,记抛物线弧![]() 的特征矩形的周长为
的特征矩形的周长为![]() .
.
①求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
②过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 与点
与点![]() 不重合.记抛物线弧
不重合.记抛物线弧![]() 的特征矩形的周长为
的特征矩形的周长为![]() .若
.若![]() ,直接写出
,直接写出![]() 的长
的长
参考答案
1.A
2.B
3.C
4.D
5.D
6.B
7.C
8.A
9.C
10.B
11.![]()
12.![]() (答案不唯一)
(答案不唯一)
13.![]()
14.![]()
15. 8 12
16.![]()
17.见解析
【详解】证明:∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
18.乙楼的高为![]()
19.(1)![]() ,补全图形见解析
,补全图形见解析
(2)![]() 人
人
(3)有提高,理由见解析
【详解】(1)解:在学期初调查数据条形图中,B组人数是![]() 人,
人,
补全条形图如下:
 ;
;
(2)解:七年级有500名学生,估计学期末七年级学生一周参与劳动时间不低于![]() 的人数有:
的人数有:
![]() (人).
(人).
答:学期末七年级学生一周参与劳动时间不低于![]() 的人数有340人;
的人数有340人;
(3)解:由表格信息可得:学期末比学期初的一周参与劳动时间的平均数,中位数,众数都增加了,
∴该校七年级学生一周参与劳动时间,学期末比学期初有提高.
20.(1)![]() (2)
(2)![]() (3)11,3(4)
(3)11,3(4)![]()
21.
(1)证明过程见详解
(2)![]() 的半径
的半径![]()
【详解】(1)解:∵![]() ,
,![]() 是
是![]() 的切线,即
的切线,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ;
;
22.
(1)购买A种水果2千克,B种水果1千克
(2)①![]() ;②
;②![]()
23.
(1)见解析
(2)![]()
(3)①见解析;②![]()
【详解】(1)证明:∵将![]() 绕点
绕点![]() 旋转得到
旋转得到![]() ,点
,点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)解:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
过![]() 作
作![]() ,
,
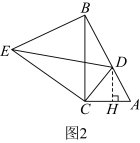
∴![]() ,
,
∴![]() ,
,
在![]() 中
中![]() ,
,
即![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
在![]() 中
中![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即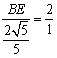 ,
,
∴![]() .
.
(3)①证明:设旋转角为![]() ,
,
则![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
②解:∵![]() ,
,
∴设![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
由①得![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
由①可得![]() ,
,
∴![]() ,
,
∴点![]() 四点共圆,
四点共圆,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴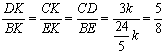 ,
,
设![]() ,
,
则![]() ,
,
根据旋转可得![]() ,
,
∴![]() ,
,
联立![]() 可得
可得![]() ,
,
∴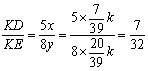 .
.
24.
(1)![]()
(2)2
(3)①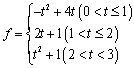 ②
②![]() 或
或![]()