2024年湖北武汉中考数学试题及答案
一、选择题(共10小题,每小题3分,共30分)
下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
2. 小美和小好同学做“石头、剪刀、布”的游戏,两人同时出相同的手势,这个事件是( )
A. 随机事件 B. 不可能事件 C. 必然事件 D. 确定性事件
3. 如图是由两个宽度相同的长方体组成的几何体,它的主视图是( )
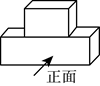
A. ![]() B.
B.  C.
C. ![]() D.
D. ![]()
4. 国家统计局2024年4月16日发布数据,今年第一季度国内生产总值接近![]() 亿元,同比增长
亿元,同比增长![]() ,国家高质量发展取得新成效.将数据
,国家高质量发展取得新成效.将数据![]() 用科学记数法表示是( )
用科学记数法表示是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 下列计算正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度h与注水时间t的函数关系的是( )
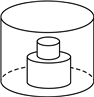
A. 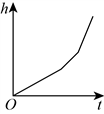 B.
B. 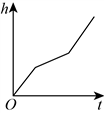 C.
C. 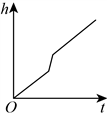 D.
D. 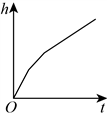
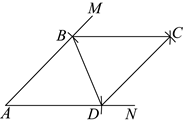
7. 小美同学按如下步骤作四边形![]() :①画
:①画![]() ;②以点
;②以点![]() 为圆心,
为圆心,![]() 个单位长为半径画弧,分别交
个单位长为半径画弧,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ;③分别以点
;③分别以点![]() ,
,![]() 为圆心,
为圆心,![]() 个单位长为半径画弧,两弧交于点
个单位长为半径画弧,两弧交于点![]() ;④连接
;④连接![]() ,
,![]() ,
,![]() .若
.若![]() ,则
,则![]() 的大小是( )
的大小是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小相同.若两辆汽车经过这个十字路口,则至少一辆车向右转的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
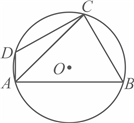
9. 如图,四边形![]() 内接于
内接于![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的半径是( )
的半径是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
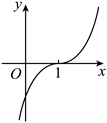
10. 如图,小好同学用计算机软件绘制函数![]() 的图象,发现它关于点
的图象,发现它关于点![]() 中心对称.若点
中心对称.若点![]() ,
,![]() ,
,![]() ,……,
,……,![]() ,
,![]() 都在函数图象上,这
都在函数图象上,这![]() 个点的横坐标从
个点的横坐标从![]() 开始依次增加
开始依次增加![]() ,则
,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C. 0 D. 1
C. 0 D. 1
二、填空题(共6小题,每小题3分,共18分)
下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.
11. 中国是世界上最早使用负数的国家.负数广泛应用到生产和生活中,例如,若零上![]()
![]() 记作
记作![]() ,则零下
,则零下![]()
![]() 记作_________
记作_________![]() .
.
12. 某反比例函数![]() 具有下列性质:当
具有下列性质:当![]() 时,y随x的增大而减小,写出一个满足条件的k的值是__________.
时,y随x的增大而减小,写出一个满足条件的k的值是__________.
13. 分式方程![]() 的解是______.
的解是______.
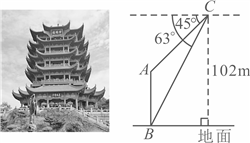
14. 黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼![]() 的高度,具体过程如下:如图,将无人机垂直上升至距水平地面
的高度,具体过程如下:如图,将无人机垂直上升至距水平地面![]() 的C处,测得黄鹤楼顶端A的俯角为
的C处,测得黄鹤楼顶端A的俯角为![]() ,底端B的俯角为
,底端B的俯角为![]() ,则测得黄鹤楼的高度是__________m.(参考数据:
,则测得黄鹤楼的高度是__________m.(参考数据:![]() )
)
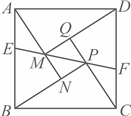
15. 如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形![]() 拼成的一个大正方形
拼成的一个大正方形![]() .直线
.直线![]() 交正方形
交正方形![]() 的两边于点
的两边于点![]() ,
,![]() ,记正方形
,记正方形![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]() .若
.若![]() ,则用含
,则用含![]() 的式子表示
的式子表示![]() 的值是___________.
的值是___________.
16. 抛物线![]() (a,b,c是常数,
(a,b,c是常数,![]() )经过
)经过![]() ,
,![]() 两点,且
两点,且![]() .下列四个结论:
.下列四个结论:
①![]() ;
;
②若![]() ,则
,则![]() ;
;
③若![]() ,则关于x的一元二次方程
,则关于x的一元二次方程 ![]() 无实数解;
无实数解;
④点![]() ,
,![]() 在抛物线上,若
在抛物线上,若![]() ,
,![]() ,总有
,总有![]() ,则
,则![]() .
.
其中正确的是__________(填写序号).
三、解答题(共8小题,共72分)
下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.
17. 求不等式组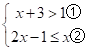 的整数解.
的整数解.
18. 如图,在![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() .
.
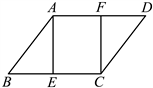
(1)求证:![]() ;
;
(2)连接![]() .请添加一个与线段相关的条件,使四边形
.请添加一个与线段相关的条件,使四边形![]() 是平行四边形.(不需要说明理由)
是平行四边形.(不需要说明理由)
19. 为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测试,每人投篮![]() 次,投中一次计
次,投中一次计![]() 分.随机抽取
分.随机抽取![]() 名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.
名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.
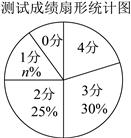
测试成绩频数分布表
成绩/分 | 频数 |
|
|
|
|
|
|
|
|
|
|
根据以上信息,解答下列问题:
(1)直接写出![]() ,
,![]() 的值和样本的众数;
的值和样本的众数;
(2)若该校九年级有![]() 名学生参加测试,估计得分超过
名学生参加测试,估计得分超过![]() 分的学生人数.
分的学生人数.
20. 如图,的中点,腰![]() 与半圆
与半圆![]() 相切于点
相切于点![]() ,底边
,底边![]() 与半圆
与半圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
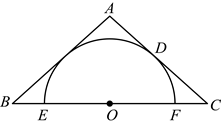
(1)求证:![]() 与半圆
与半圆![]() 相切;
相切;
(2)连接![]() .若
.若![]() ,
,![]() ,求
,求![]() 的值.
的值.
21. 如图是由小正方形组成的![]() 网格,每个小正方形的顶点叫做格点.
网格,每个小正方形的顶点叫做格点.![]() 三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条
三个顶点都是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条
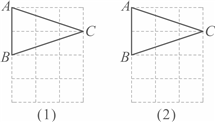
(1)在图(1)中,画射线![]() 交
交![]() 于点D,使
于点D,使![]() 平分
平分![]() 的面积;
的面积;
(2)在(1)的基础上,在射线![]() 上画点E,使
上画点E,使![]() ;
;
(3)在图(2)中,先画点F,使点A绕点F顺时针旋转![]() 到点C,再画射线
到点C,再画射线![]() 交
交![]() 于点G;
于点G;
(4)在(3)的基础上,将线段![]() 绕点G旋转
绕点G旋转![]() ,画对应线段
,画对应线段![]() (点A与点M对应,点B与点N对应).
(点A与点M对应,点B与点N对应).
22. 16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系,分别得到抛物线![]() 和直线
和直线![]() .其中,当火箭运行的水平距离为
.其中,当火箭运行的水平距离为![]() 时,自动引发火箭的第二级
时,自动引发火箭的第二级
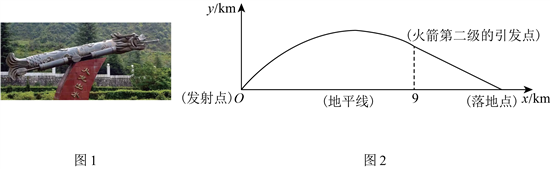
(1)若火箭第二级的引发点的高度为![]() .
.
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低![]() ,求这两个位置之间的距离.
,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过![]() .
.
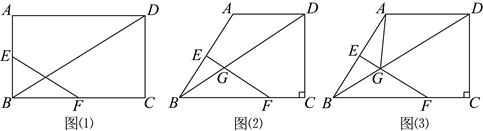
23. 问题背景:如图(1),在矩形![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() ,求证:
,求证:![]() .
.
问题探究:如图(2),在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() .
.
问题拓展:如图(3),在“问题探究”的条件下,连接![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
24. 抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的右边),交
的右边),交![]() 轴于点
轴于点![]() .
.
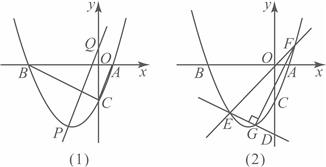
(1)直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)如图(1),连接![]() ,
,![]() ,过第三象限的抛物线上的点
,过第三象限的抛物线上的点![]() 作直线
作直线![]() ,交y轴于点
,交y轴于点![]() .若
.若![]() 平分线段
平分线段![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图(2),点![]() 与原点
与原点![]() 关于点
关于点![]() 对称,过原点的直线
对称,过原点的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴下方),线段
轴下方),线段![]() 交抛物线于另一点
交抛物线于另一点![]() ,连接
,连接![]() .若
.若![]() ,求直线
,求直线![]() 的解析式
的解析式
参考答案
一、选择题(共10小题,每小题3分,共30分)
下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
【1题答案】
【答案】C
【2题答案】
【答案】A
【3题答案】
【答案】B
【4题答案】
【答案】C
【5题答案】
【答案】B
【6题答案】
【答案】D
【7题答案】
【答案】C
【8题答案】
【答案】D
【9题答案】
【答案】A
【10题答案】
【答案】D
二、填空题(共6小题,每小题3分,共18分)
下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.
【11题答案】
【答案】![]()
【12题答案】
【答案】1(答案不唯一)
【13题答案】
【答案】![]()
【14题答案】
【答案】51
【15题答案】
【答案】![]()
【16题答案】
【答案】②③④
三、解答题(共8小题,共72分)
下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.
【17题答案】
【答案】整数解为:![]()
【18题答案】
【答案】(1)见解析 (2)添加![]() (答案不唯一)
(答案不唯一)
【19题答案】
【答案】(1)![]() ,
,![]() ,众数为
,众数为![]() 分
分
(2)该校九年级有![]() 名学生参加测试,估计得分超过
名学生参加测试,估计得分超过![]() 分的学生人数为
分的学生人数为![]() 人
人
【20题答案】
【答案】(1)见解析 (2)![]()
【21题答案】
【答案】(1)作图见解析
(2)作图见解析 (3)作图见解析
(4)作图见解析
【22题答案】
【答案】(1)①![]() ,
,![]() ;②
;②![]()
(2)![]()
【23题答案】
【答案】问题背景:见解析;问题探究:见解析;问题拓展:![]()
【24题答案】
【答案】(1)![]() ,
,![]() ,
,![]()
(2)![]()
(3)![]()
