2025年山东烟台中考数学试题及答案

2025年山东烟台中考数学试题及答案

　　一、选择题（本大题共10个小题，每小题3分，满分30分．每小题都给出标号为A，B，C，D四个备选答案，其中有且只有一个是正确的）

　　1．|-3|的倒数是（   ）

　　A．3B．C．-3D．

　　2．2025年4月24日，神舟二十号载人飞船成功发射，以壮丽升空将第10个中国航天日从纪念变为庆祝．下列航天图案是中心对称图形的是（   ）

　　A．B．C．D．

　　3．下列计算正确的是（   ）

　　A．B．

　　C．D．

　　4．如图是社团小组运用打印技术制作的模型，它的左视图是（   ）

　　A．B．C．D．

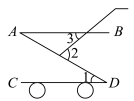
　　5．如图是一款儿童小推车的示意图，若，，，则的度数为（   ）

　　A．B．C．D．

　　6．求一组数据方差的算式为：．由算式提供的信息，下列说法错误的是（   ）

　　A．的值是5

　　B．该组数据的平均数是7

　　C．该组数据的众数是6

　　D．若该组数据加入两个数7，7，则这组新数据的方差变小

　　7．某商场打折销售一款风扇，若按标价的六折出售，则每台风扇亏损10元；若按标价的九折出售，则每台风扇盈利95元．这款风扇每台的标价为（   ）

　　A．350元B．320元C．270元D．220元

　　8．如图，菱形的顶点在轴正半轴上，，反比例函数的图象过点和菱形的对称中心，则的值为（   ）

　　A．4B．C．2D．

　　9．如图，二次函数的部分图象与轴的一个交点位于和之间，顶点的坐标为．下列结论：①；②对于任意实数，都有；③；④若该二次函数的图象与轴的另一个交点为，且是等边三角形，则．其中所有正确结论的序号是（   ）

　　A．①②B．①③C．①④D．①③④

　　10．如图，在中，，，是角平分线．点从点出发，沿方向向点运动，连接，点在上，且．设，，若y关于x的函数图象过点，则该图象上最低点的坐标为（   ）

　　A．B．C．D．

　　二、填空题（本大题共6个小题，每小题3分，满分18分）

　　11．2025年2月2日是第29个“世界湿地日”，主题是“保护湿地共筑未来”．国家林草局公布的最新数据显示，全国湿地面积稳定保持在56350000公顷以上．将数据56350000用科学记数法表示为        ．

　　12．实数的整数部分为        ．

　　13．因式分解：        ．

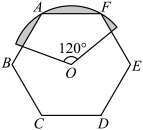
　　14．如图，正六边形的边长为4，中心为点，以点为圆心，以长为半径作圆心角为的扇形，则图中阴影部分的面积为      ．

　　15．如图，在平面直角坐标系中，点的坐标为，的顶点的坐标为．以点为位似中心作与位似，相似比为2，且与位于点同侧；以点为位似中心作与位似，相似比为2，且与位于点同侧……按照以上规律作图，点的坐标为      ．

　　16．如图，在菱形中，，对角线．点M从点A出发，沿方向以的速度向点C运动，同时，点N从点C出发，沿方向以的速度向点D运动，当一点到达终点时，另一点随之停止运动，连接，交于点P．在此过程中，点P的运动路径长为         ．

　　三、解答题（本大题共8个小题，满分72分）

　　17．先化简，再求值：，其中．

　　18．2025年4月19日，烟台市民文化艺术季启幕．某校带领甲、乙两个社团参观甲骨学发展史馆，领略殷商文明甲骨文化穿越千年的不朽魅力．活动结束后，两个社团进行了一次满分为10分的甲骨学发展史测试，并对所有学生的成绩进行了收集、整理、分析，信息如下：

　　①甲社团的成绩（单位：分）情况如下：

　　6，6，6，6，7，7，7，7，6，7，7，6，7，8，8，8，8，9，8，8，9，9，9，8，8，9，9，9，7，9，6，9，9，10，8，8，9，9，10，10．

　　②乙社团的平均成绩为（分）．

　　③将两个社团的成绩绘制成如下不完整的统计图：

　　根据以上信息，解决下列问题：

　　(1)将条形统计图补充完整；

　　(2)成绩为8分的学生在_______社团的排名更靠前（填“甲”或“乙”）；

　　(3)已知甲社团的满分学生中有两名女生，现从甲社团满分学生中随机抽取两人，参加甲骨学发展史宣讲活动．请用树状图或表格求所抽取的两人恰好是一名男生和一名女生的概率

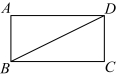
　　19．如图，是矩形的对角线，请按以下要求解决问题：

　　(1)利用尺规作，使与关于直线成轴对称（不写作法，保留作图痕迹）；

　　(2)在（1）的条件下，若交于点，，，求的长．

　　20．2025年6月5日是第54个“世界环境日”，为打造绿色低碳社区，某社区决定购买甲、乙两种太阳能路灯安装在社区公共区域，升级改造现有照明系统．已知购买1盏甲种路灯和2盏乙种路灯共需220元，购买3盏甲种路灯比4盏乙种路灯的费用少140元．

　　(1)求甲、乙两种路灯的单价；

　　(2)该社区计划购买甲、乙两种路灯共40盏，且甲种路灯的数量不超过乙种路灯数量的，请通过计算设计一种购买方案，使所需费用最少．

　　21．【综合与实践】

　　烟台山灯塔被誉为“黄海夜明珠”，它坐落在烟台山上，为过往船只提供导航服务．为了解渔船海上作业情况，某日，数学兴趣小组开展了实践探究活动．

　　如图，一艘渔船自东向西以每小时海里的速度向码头航行，小组同学收集到以下信息：

　　请根据以上信息，解答下列问题：

　　(1)求渔船在航行过程中到灯塔的最短距离；

　　(2)若不改变航行速度，请通过计算说明渔船能否在浓雾到来前到达码头（参考数据：，，，，，）．

　　22．如图，内接于，，点在线段的延长线上，且，连接．

　　(1)求证：是的切线；

　　(2)当，时，求的长及的半径．

　　23．【问题呈现】

　　如图1，已知是正方形外一点，且满足，探究，，三条线段的数量关系．

　　小颖通过观察、分析、思考，形成了如下思路：

　　思路一：如图2，构造与全等，从而得出与的数量关系；

　　思路二：如图3，构造与全等，从而得出与的数量关系．

　　（1）请参考小颖的思路，直接写出与的数量关系______________；

　　【类比探究】

　　（2）如图4，若是正五边形外一点，且满足，，，求的长度（结果精确到，参考数据：，，，）；

　　【拓展延伸】

　　（3）如图5，若是正十边形外一点，且满足，则，，三条线段的数量关系为_________（结果用含有锐角三角函数的式子表示）．

　　24．如图，抛物线与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，，，D是直线上方抛物线上一动点，作交于点E，垂足为点F，连接．

　　(1)求抛物线的表达式；

　　(2)设点D的横坐标为，

　　①用含有的代数式表示线段的长度；

　　②是否存在点D，使是等腰三角形?若存在，请求出所有满足条件的点D的坐标；若不存在，请说明理由；

　　(3)连接，将线段绕点按顺时针方向旋转得到线段，连接，请直接写出线段长度的最小值

参考答案

　　1．B

　　2．D

　　3．B

　　4．C

　　5．A

　　6．C

　　7．A

　　8．D

　　9．D

　　10．B

　　11．

　　12．

　　13．

　　14．

　　15．##

　　16．

　　17．，

　　18．(1)补全图形见解析

　　(2)成绩为8分的学生在乙社团的排名更靠前

　　(3)

　　【详解】（1）解：∵由统计数据可得：甲社团满分分有3人；乙社团分有人；补全图形如下：

　　；

　　19．(1)作图见解析

　　(2)

　　【详解】（1）解：如图，即为所求作的三角形；

　　由作图可得：，，，

　　∴，

　　∴即为所求作的三角形；

　　20．(1)甲、乙两种路灯的单价分别为元，元

　　(2)购买甲种路灯盏，购买乙种路灯盏，费用最少

　　21．(1)渔船在航行过程中到灯塔的最短距离为海里

　　(2)不改变航行速度，渔船能在浓雾到来前到达码头

　　22．(1)见解析

　　(2)；的半径为

　　【详解】（1）证明：如图，连接并延长交于点，连接，

　　∵，

　　∴

　　∴

　　又∵，

　　∴

　　∴

　　∵

　　∴

　　∴

　　∵是直径

　　∴

　　∴即

　　∴是的切线；

　　23．（1）；（2）；（3）

　　24．(1)

　　(2)①；②存在，或或

　　(3)