2025年江苏苏州中考数学试题及答案
一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卡相对应的位置上.
1.下列实数中,比2小的数是( )
A.5B.4C.3D.-1
2.如图,将直角三角形绕它的一条直角边所在直线旋转一周后形成的几何体是( )

A.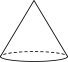 B.
B.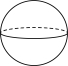 C.
C.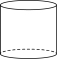 D.
D.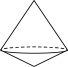
3.据人民网消息2025年第一季度,苏州市货物贸易进出口总值达63252000万元,其中,出品40317000万元,创历史同期新高,同比增长![]() .数据40317000用科学记数法可表示为( )
.数据40317000用科学记数法可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列运算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
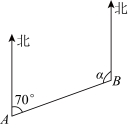
5.如图,在![]() 两地间修一条笔直的公路,从A地测得公路的走向北偏东
两地间修一条笔直的公路,从A地测得公路的走向北偏东![]() .若
.若![]() 两地同时开工,要使公路准确接通,则
两地同时开工,要使公路准确接通,则![]() 的度数应为( )
的度数应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.一只不透明的袋子中,装有3个白球和若干个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,摸到白球的概率为![]() ,则红球的个数为( )
,则红球的个数为( )
A.1B.2C.3D.4
7.声音在空气中传播的速度随温度的变化而变化,科学家测得一定温度下声音传播的速度![]() 与温度
与温度![]() 部分对应数值如下表:
部分对应数值如下表:
温度 | | 0 | 10 | 30 |
声音传播的速度 | 324 | 330 | 336 | 348 |
研究发现![]() 满足公式
满足公式![]() (
(![]() 为常数,且
为常数,且![]() ).当温度t为
).当温度t为![]() 时,声音传播的速度v为( )
时,声音传播的速度v为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
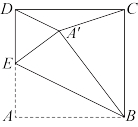
8.如图,在正方形![]() 中,E为边
中,E为边![]() 的中点,连接
的中点,连接![]() ,将
,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,连接
,连接![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.![]() B.
B.![]()
C.![]() 的面积
的面积![]() 的面积D.四边形
的面积D.四边形![]() 的面积
的面积![]() 的面积
的面积
二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相对应的位置上.
9.因式分解:![]() .
.
10.某篮球队在一次联赛中共进行了6场比赛,得分依次为:![]() .这组数据的众数为 .
.这组数据的众数为 .
11.若![]() ,则代数式
,则代数式![]() 的值为 .
的值为 .
12.过![]() 两点画一次函数
两点画一次函数![]() 的图像,已知点A的坐标为
的图像,已知点A的坐标为![]() ,则点B的坐标可以为 .(填一个符合要求的点的坐标即可)
,则点B的坐标可以为 .(填一个符合要求的点的坐标即可)
13.已知![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两个实数根,其中
的两个实数根,其中![]() ,则
,则![]()
14.“苏州之眼”摩天轮是亚洲最大的水上摩天轮,共设有28个回转式太空舱全景轿厢,其示意图如图所示.该摩天轮高![]() (即最高点离水面平台
(即最高点离水面平台![]() 的距离),圆心O到
的距离),圆心O到![]() 的距离为
的距离为![]() ,摩天轮匀速旋转一圈用时
,摩天轮匀速旋转一圈用时![]() .某轿厢从点A出发,
.某轿厢从点A出发,![]() 后到达点B,此过程中,该轿厢所经过的路径(即
后到达点B,此过程中,该轿厢所经过的路径(即![]() )长度为
)长度为 ![]() .(结果保留
.(结果保留![]() )
)

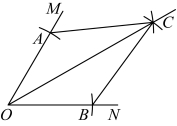
15.如图,![]() ,以O为圆心,2为半径画弧,分别交
,以O为圆心,2为半径画弧,分别交![]() 于
于![]() 两点,再分别以
两点,再分别以![]() 为圆心,
为圆心,![]() 为半径画弧,两弧在
为半径画弧,两弧在![]() 内部相交于点C,作射线
内部相交于点C,作射线![]() ,连接
,连接![]() ,则
,则![]() .(结果保留根号)
.(结果保留根号)
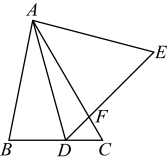
16.如图,在![]() 中,
中,![]() 是线段
是线段![]() 上一点(不与端点
上一点(不与端点![]() 重合),连接
重合),连接![]() ,以
,以![]() 为边,在
为边,在![]() 的右侧作等边三角形
的右侧作等边三角形![]() ,线段
,线段![]() 与线段
与线段![]() 交于点F,则线段
交于点F,则线段![]() 长度的最大值为 .
长度的最大值为 .
三、解答题:本大题共11小题,共82分.把解答过程写在答题卡相对应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.
17.计算:![]() .
.
18.解不等组: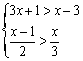
19.先化简,再求值:![]() ,其中
,其中![]() .
.
20.为了弘扬社会主义核心价值观,学校决定组织“立鸿鹄之志,做有为少年”主题观影活动,建议同学们利用周末时间自主观看.现有![]() 共3部电影,甲、乙2位同学分别从中任意选择1部电影观看.
共3部电影,甲、乙2位同学分别从中任意选择1部电影观看.
(1)甲同学选择A电影的概率为________;
(2)求甲、乙2位同学选择不同电影的概率.(请用画树状图或列表等方法说明理由)
21.如图,C是线段![]() 的中点,
的中点,![]() .
.
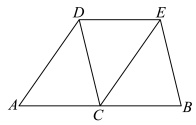
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
22.随着人工智能的快速发展,初中生使用![]() 大模型辅助学习快速普及,并呈现出多样化趋势.某研究性学习小组采用简单随机抽样的方法,对本校九年级学生一周使用
大模型辅助学习快速普及,并呈现出多样化趋势.某研究性学习小组采用简单随机抽样的方法,对本校九年级学生一周使用![]() 大模型辅助学习的时间(用x表示,单位:
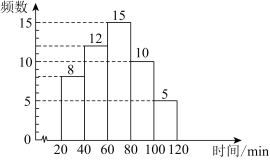
大模型辅助学习的时间(用x表示,单位:![]() )进行了抽样调查,把所得的数据分组整理,并绘制成频数分布直方图:
)进行了抽样调查,把所得的数据分组整理,并绘制成频数分布直方图:
抽取的学生一周使用![]() 大模型辅助学习时间频率分布表
大模型辅助学习时间频率分布表
组别 | 时间 | 频率 |
A | | |
B | | |
C | | |
D | | |
E | | |
合计 | 1 | |

根据提供的信息回答问题:
(1)请把频数分布直方图补充完整(画图后标注相应数据);
(2)调查所得数据的中位数落在________组(填组别);
(3)该校九年级共有750名学生,根据抽样调查结果,估计该校九年级学生一周使用![]() 大模型辅助学习的时间不少于
大模型辅助学习的时间不少于![]() 的学生人数.
的学生人数.
23.如图,一次函数![]() 的图象与x轴,y轴分别交于A,B两点,与反比例函数
的图象与x轴,y轴分别交于A,B两点,与反比例函数![]() 的图象交于点C,过点B作x轴的平行线与反比例函数
的图象交于点C,过点B作x轴的平行线与反比例函数![]() 的图象交于点D,连接
的图象交于点D,连接![]() .
.
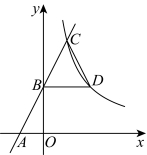
(1)求A,B两点的坐标;
(2)若![]() 是以
是以![]() 为底边的等腰三角形,求k的值.
为底边的等腰三角形,求k的值.
24.综合与实践
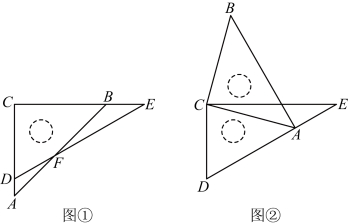
小明同学用一副三角板进行自主探究.如图,![]() 中,
中,![]() ,
,![]() 中,
中,![]() .
.
【观察感知】
(1)如图①,将这副三角板的直角顶点和两条直角边分别重合,![]() 交于点F,求
交于点F,求![]() 的度数和线段
的度数和线段![]() 的长.(结果保留根号)
的长.(结果保留根号)
【探索发现】
(2)在图①的基础上,保持![]() 不动,把
不动,把![]() 绕点C按逆时针方向旋转一定的角度,使得点A落在边
绕点C按逆时针方向旋转一定的角度,使得点A落在边![]() 上(如图②).
上(如图②).
①求线段![]() 的长;(结果保留根号)
的长;(结果保留根号)
②判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
25.如图,在四边形![]() 中,
中,![]() .以
.以![]() 为直径的
为直径的![]() 经过点D,且与边
经过点D,且与边![]() 交于点E,连接
交于点E,连接![]() .
.
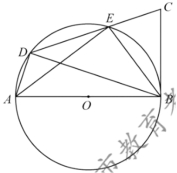
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
26.两个智能机器人在如图所示的![]() 区域工作,
区域工作,![]() ,
,![]() ,直线
,直线![]() 为生产流水线,且
为生产流水线,且![]() 平分
平分![]() 的面积(即D为
的面积(即D为![]() 中点).机器人甲从点A出发,沿
中点).机器人甲从点A出发,沿![]() 的方向以
的方向以![]() 的速度匀速运动,其所在位置用点P表示,机器人乙从点B出发,沿
的速度匀速运动,其所在位置用点P表示,机器人乙从点B出发,沿![]() 的方向以
的方向以![]() 的速度匀速运动,其所在位置用点Q表示.两个机器人同时出发,设机器人运动的时间为
的速度匀速运动,其所在位置用点Q表示.两个机器人同时出发,设机器人运动的时间为![]() ,记点P到
,记点P到![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() ,点Q到
,点Q到![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() .当机器人乙到达终点时,两个机器人立即同时停止运动,此时
.当机器人乙到达终点时,两个机器人立即同时停止运动,此时![]() 与t的部分对应数值如下表
与t的部分对应数值如下表![]() :
:
| 0 | | | 5.5 |
| 0 | 16 | 16 | 0 |
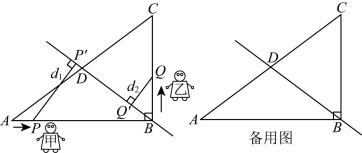
(1)机器人乙运动的路线长为________m;
(2)求![]() 的值;
的值;
(3)当机器人甲、乙到生产流水线![]() 的距离相等(即
的距离相等(即![]() )时,求t的值.
)时,求t的值.
27.如图,二次函数![]() 的图像与x轴交于
的图像与x轴交于![]() 两点(点A在点B的左侧),与y轴交于点C,作直线
两点(点A在点B的左侧),与y轴交于点C,作直线![]() 为二次函数
为二次函数![]() 图像上两点.
图像上两点.
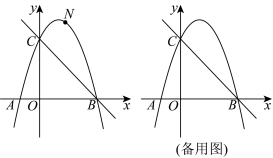
(1)求直线![]() 对应函数的表达式;
对应函数的表达式;
(2)试判断是否存在实数m使得![]() .若存在,求出m的值;若不存在,请说明理由.
.若存在,求出m的值;若不存在,请说明理由.
(3)已知P是二次函数![]() 图像上一点(不与点
图像上一点(不与点![]() 重合),且点P的横坐标为
重合),且点P的横坐标为![]() ,作
,作![]() .若直线
.若直线![]() 与线段
与线段![]() 分别交于点
分别交于点![]() ,且
,且![]() 与
与![]() 的面积的比为
的面积的比为![]() ,请直接写出所有满足条件的m的值
,请直接写出所有满足条件的m的值
参考答案
1.D
2.A
3.B
4.C
5.C
6.B
7.B
8.D
9.![]()
10.71
11.![]()
12.![]() (答案不唯一)
(答案不唯一)
13.![]()
14.![]()
15.![]()
16.![]() ##0.75
##0.75
17.10
18.![]()
19.![]() ,2
,2
20.(1)![]()
(2)![]()
21.
(1)详见解析
(2)8
【详解】(1)证明:![]() 是线段
是线段![]() 的中点,
的中点,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() .
.
22.
(1)图见解析
(2)C
(3)该校九年级学生一周使用![]() 大模型辅助学习的时间不少于
大模型辅助学习的时间不少于![]() 的学生人数约为450人
的学生人数约为450人
【详解】(1)解:![]() .
.
D组人数:![]() 人.
人.
如图为所求:
23.(1)![]() ,
,![]()
(2)![]()
24.
(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]()
25.(1)详见解析
(2)![]() .
.
【详解】(1)证明:∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 为
为![]() 的切线;
的切线;
26.(1)55
(2)![]()
(3)![]() 或
或![]()
27.(1)![]()
(2)不存在,理由见解析
(3)![]() 或
或![]()
【详解】
(2)不存在实数m使得![]() ,理由如下:
,理由如下:
方法一:![]() 为二次函数
为二次函数![]() 图像上两点,
图像上两点,
![]() ,
,
![]() .
.
![]() .
.
配方,得![]() .
.
∴当![]() 时,
时,![]() 有最大值为
有最大值为![]() .
.
![]() ,
,
∴不存在实数m使得![]() .
.
方法二:由方法一,得![]() .
.
当![]() 时,
时,![]() ,即
,即![]() .
.
![]() ,
,
∴方程没有实数根.
![]() 不存在实数m使得
不存在实数m使得![]()
