2025年江苏扬州中考数学试题及答案

2025年江苏扬州中考数学试题及答案

　　一、选择题（本大题共有8小题，每小题3分，共24分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将该选项的字母代号填涂在答题卡相应位置上）

　　1．下列温度中，比-3℃低的温度是（   ）

　　A．-5℃B．-2℃C．0℃D．2℃

　　2．窗棂是中国传统木构建筑的重要元素，既散发着古典之韵，又展现了几何之美．下列窗棂图案中，是轴对称图形但不是中心对称图形的是（   ）

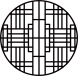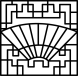　　A．B．C．D．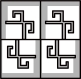　

　　3．下列说法不正确的是（   ）

　　A．明天下雨是随机事件

　　B．调查长江中现有鱼的种类，适宜采用普查的方式

　　C．描述一周内每天最高气温的变化情况，适宜采用折线统计图

　　D．若甲组数据的方差，乙组数据的方差，则乙组数据更稳定

　　4．关于一元二次方程的根的情况，下列结论正确的是（   ）

　　A．有两个不相等的实数根B．有两个相等的实数根

　　C．没有实数根D．无法判断根的情况

　　5．如图，数轴上点表示的数可能是（   ）

　　A．B．C．D．

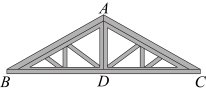
　　6．在如图的房屋人字梁架中，，点在上，下列条件不能说明的是（   ）

　　A．B．C．D．平分

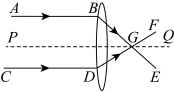
　　7．如图，平行于主光轴的光线和经过凸透镜折射后，折射光线，交于主光轴上一点，若，，则的度数是（   ）

　　A．B．C．D．

　　8．已知，则一次函数的图象不经过（   ）

　　A．第一象限B．第二象限C．第三象限D．第四象限

　　二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）

　　9．2025年3月30日，扬州鉴真半程马拉松暨大运河马拉松系列赛在市民中心广场鸣枪开跑，约30000名跑者用脚步丈量千年古城，用拼搏诠释无限热爱．将数据30000用科学记数法表示为      ．

　　10．分解因式：      ．

　　11．计算：      ．

　　12．若，则代数式的值是      ．

　　13．若多边形的每个内角都是，则这个多边形的边数为      ．

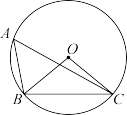
　　14．如图，点，，在上，，则      ．

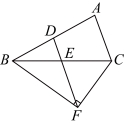
　　15．如图，在中，点，分别是边，的中点，点在线段的延长线上，且，若，，则的长是      ．

　　16．清代扬州数学家罗士琳痴迷于勾股定理的研究，提出了推算勾股数的“罗士琳法则”．法则的提出，不仅简化了勾股数的生成过程，也体现了中国传统数学在数论领域的贡献．由此法则写出了下列几组勾股数：①3，4，5；②5，12，13；③7，24，25；④9，40，41；……根据上述规律，写出第⑤组勾股数为      ．

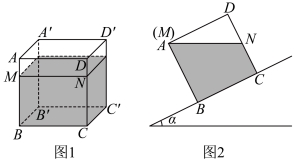
　　17．如图1，棱长为的密封透明正方体容器水平放置在桌面上，其中水面高度．将此正方体放在坡角为的斜坡上，此时水面恰好与点齐平，其主视图如图2所示，则      ．

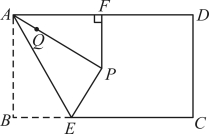
　　18．如图，在矩形中，，，点是边上的动点，将沿直线翻折得到，过点作，垂足为，点是线段上一点，且．当点从点运动到点时，点运动的路径长是      ．

　　三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

　　19．计算：

　　(1)；

　　(2)．

　　20．解不等式组，并写出它的所有负整数解．

　　21．为角逐市校园“音乐达人”大赛，小红和小丽参加了校内选拔赛，10位评委的评分情况如下（单位：分）．

　　表1评委评分数据

　　表2评委评分数据分析

　　根据以上信息，回答下列问题：

　　(1)表2中______，______，______；

　　(2)你认为小红和小丽谁的成绩较好？请说明理由．

　　22．为打造活力校园，某校在大课间开展了丰富多彩的活动，现有4种体育类活动供学生选择：A．羽毛球，B．乒乓球，C．花样跳绳，D．踢毽子，每名学生只能选择其中一种体育活动．

　　(1)若小明在这4种体育活动中随机选择，则选中“乒乓球”的概率是______；

　　(2)请用画树状图或列表的方法，求小明和小聪随机选择选到同一种体育活动的概率．

　　23．某文创商店推出甲、乙两款具有纪念意义和实用价值的书签，已知甲款书签价格是乙款书签价格的倍，且用100元购买甲款书签的数量比用128元购买乙款书签的数量少3个，求这两款书签的单价．

　　24．如图，在平面直角坐标系中，反比例函数的图象与一次函数的图象交于点，

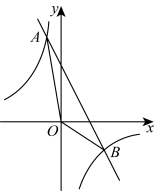
　　(1)求反比例函数、一次函数的表达式；

　　(2)求的面积．

　　25．如图，在中，对角线的垂直平分线与边，分别相交于点，．

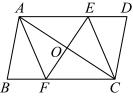
　　(1)求证：四边形是菱形；

　　(2)若，，平分，求的长．

　　26．材料的疏水性

　　扬州宝应是荷藕之乡．“微风忽起吹莲叶，青玉盘中泻水银”，莲叶上的水滴来回滚动，不易渗入莲叶内部，这说明莲叶具有较强的疏水性．疏水性是指材料与水相互排斥的一种性质．

　　【概念理解】

　　材料疏水性的强弱通常用接触角的大小来描述．材料上的水滴可以近似的看成球或球的一部分，经过球心的纵截面如图1所示，接触角是过固、液、气三相接触点（点或点）所作的气?液界线的切线与固?液界线的夹角，图1中的就是水滴的一个接触角．

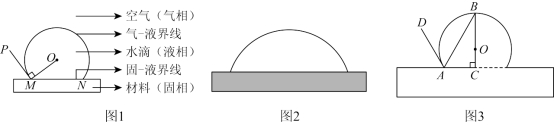
　　（1）请用无刻度的直尺和圆规作出图2中水滴的一个接触角，并用三个大写字母表示接触角；（保留作图痕迹，写出必要的文字说明）

　　（2）材料的疏水性随着接触角的变大而______（选填“变强”“不变”“变弱”）．

　　【实践探索】

　　实践中，可以通过测量水滴经过球心的高度和底面圆的半径，求出的度数，进而求出接触角的度数（如图3）．

　　（3）请探索图3中接触角与之间的数量关系（用等式表示），并说明理由．

　　【创新思考】

　　（4）材料的疏水性除了用接触角以及图3中与相关的量描述外，还可以用什么量来描述，请你提出一个合理的设想，并说明疏水性随着此量的变化而如何变化．

　　27．如图，在平面直角坐标系中，二次函数的图象（记为）与轴交于点，，与轴交于点，二次函数的图象（记为）经过点，．直线与两个图象，分别交于点，，与轴交于点．

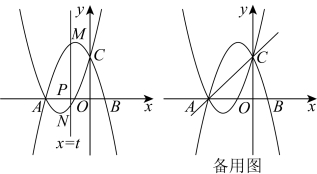
　　(1)求，的值．

　　(2)当点在线段上时，求的最大值．

　　(3)设点，到直线的距离分别为，．当时，对应的值有______个；当时，对应的值有______个；当时，对应的值有______个；当时，对应的值有______个．

　　28．问题：如图1，点为正方形内一个动点，过点作，，矩形的面积是矩形面积的2倍，探索的度数随点运动的变化情况．

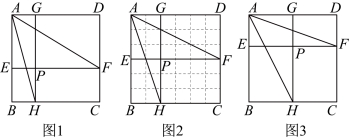
　　【从特例开始】

　　（1）小玲利用正方形网格画出了一个符合条件的特殊图形（如图2），请你仅用无刻度的直尺连接一条线段，由此可得此图形中______；

　　（2）小亮也画出了一个符合条件的特殊图形（如图3），其中，，，求此图形中的度数；

　　【一般化探索】

　　（3）利用图1，探索上述问题中的度数随点运动的变化情况，并说明理由

参考答案

　　1．A

　　2．C

　　3．B

　　4．A

　　5．C

　　6．B

　　7．C

　　8．D

　　9．

　　10．

　　11．##

　　12．1

　　13．9

　　14．40

　　15．6

　　16．

　　17．

　　18．

　　19．(1)

　　(2)

　　20．不等式组的解集为，它的所有负整数解为

　　21．(1)；7；8

　　(2)小丽的成绩较好，理由见解析

　　22．(1)

　　(2)

　　23．乙款书签价格为16元，甲款书签价格为20元

　　24．(1)反比例函数的表达式为，一次函数的表达式为

　　(2)8

　　25．

　　(1)见解析

　　(2)

　　【详解】（1）证明：∵四边形是平行四边形，

　　∴，

　　∴，

　　∵对角线的垂直平分线是，

　　∴，

　　∵，

　　∴，

　　∴，

　　∴四边形是平行四边形，

　　∵，

　　∴四边形是菱形；

　　26．（1）图见解析（2）变强（3），理由见解析（4）见解析（答案不唯一）

　　27．(1)，

　　(2)

　　(3)2，0，4，无数

　　28．（1）作图见解析，45；（2）；（3）随点的运动，的度数不变，且为

　　【详解】解：（1）如图，即为所求：

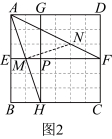
　　连接与格线的交点记为，

　　由网格可得，，

　　∴，

　　∴，

　　∵，

　　∴,

　　∴为格点，同理为格点，

　　∵，，，

　　∴，，

　　∴，

　　∴为等腰直角三角形，

　　∴；

　　故答案为：45；