2025年上海中考数学试题及答案
一、选择题(本大题共6题,每题4分,满分24分)
1.下列代数式中,计算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.用代数式表示![]() 与
与![]() 差的平方,正确的是( )
差的平方,正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列函数中,为正比例函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.某学校组织了一场体育测试,现抽出60个人的体育考试分数,并对此进行统计,如图所示.关于这60人的分数,下列说法正确的是( )

A.中位数是12B.中位数是75C.众数是21D.众数是85
5.在正方形![]() 中,
中,![]() 的值为( )
的值为( )
A.![]() B.1C.
B.1C.![]() D.2
D.2
6.在锐角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 的外接圆为
的外接圆为![]() ,且半径为5,边
,且半径为5,边![]() 中点为
中点为![]() ,如果以
,如果以![]() 为圆心的圆与
为圆心的圆与![]() 相交,那么
相交,那么![]() 的半径可以为( )
的半径可以为( )
A.2B.5C.8D.9
二、填空题(本大题共12题,每题4分,满分48分)
7.分解因式:![]() .
.
8.不等式组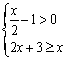 的解集为 .
的解集为 .
9.已知关于![]() 的一元二次方程
的一元二次方程![]() 没有实数根,则
没有实数根,则![]() 的取值范围是
的取值范围是
10.已知一个反比例函数在各个象限内,![]() 随
随![]() 的增大而减小,那么这个反比例函数的解析式可以是 .(只需写出一个)
的增大而减小,那么这个反比例函数的解析式可以是 .(只需写出一个)
11.方程![]() 的解为 .
的解为 .
12.将函数![]() 的图像向下平移2个单位后,得到的新函数的解析式为 .
的图像向下平移2个单位后,得到的新函数的解析式为 .
13.小明与小杰在玩卡牌游戏,已知小明手里有1.2,3,4四张牌,小杰手里有2,4,6,8四张牌,小明从小杰手里抽出一张牌,如果抽到小杰手中四张卡牌中的任意一张概率都相等,那么小明抽出的这张卡牌中,和自己手中某一张卡牌的数字一样的概率为 .
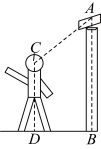
14.某公司需要员工上班时通过门禁,在门禁上方设置了人脸扫描仪,已知扫描仪(线段![]() )的竖直高度2.7米,某人(线段
)的竖直高度2.7米,某人(线段![]() )身高为1.8米,扫描仪测得
)身高为1.8米,扫描仪测得![]() ,那么该人与扫描仪的水平距离为 米.(备用数据:
,那么该人与扫描仪的水平距离为 米.(备用数据:![]() ,
,![]() ,
,![]() ,精确到
,精确到![]() 米)
米)
15.为了解乘客到达高铁站后离开的方式.某地开展问卷调查,共收到有效答复2000张,调查结果如图所示.如果当地每天离开高铁站的人数约为1.8万人,那么当地每天乘坐出租车离开的人数大约为 .

16.据报道,我国某科研团队近期成功研制出一种新闪存器件,其快速擦写速度全球领先.已知一皮秒等于![]() 秒,该器件执行一次擦写需要400皮秒,则该器件一秒可以擦写 次(科学记数法表示).
秒,该器件执行一次擦写需要400皮秒,则该器件一秒可以擦写 次(科学记数法表示).
17.在矩形![]() 中,
中,![]() 在边
在边![]() 上,
上,![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,联结
,联结![]() ,
,![]() ,如果四边形
,如果四边形![]() 是菱形,那么
是菱形,那么![]() 的值为 .
的值为 .
18.已知一个圆与一个角的两边各有两个公共点,且在两边上截得的两条弦正好是该圆内接正五边形的两条边,那么这个角的大小是
三、解答题(本大题共7题,满分78分)
19.计算:![]() .
.
20.解方程:![]() .
.
21.已知学校热水器有一个可以储200升(![]() )水的储水装置,且水在装满储水装置时会自动停止,如图所示为储水量
)水的储水装置,且水在装满储水装置时会自动停止,如图所示为储水量![]() 与加水时间
与加水时间![]() 的关系,已知温度
的关系,已知温度![]() (单位:
(单位:![]() )与
)与![]() 的关系为:
的关系为:![]() .
.

(1)求![]() 关于
关于![]() 的函数解析式并写出定义域;
的函数解析式并写出定义域;
(2)当水加满时,储水装置内水的温度为多少?
22.小明正在进行探究活动:分割梯形并将其拼成等腰三角形,请你帮他一起探究.

(1)如图(1)所示,在梯形![]() 中,
中,![]() ,
,![]() .设
.设![]() 为边
为边![]() 中点,将
中点,将![]() 绕点
绕点![]() 旋转
旋转![]() ,点
,点![]() 旋转至点
旋转至点![]() 的位置,得到的
的位置,得到的![]() 是等腰三角形,其中
是等腰三角形,其中![]() ,设
,设![]() ,求边
,求边![]() 的长(用
的长(用![]() 表示);
表示);
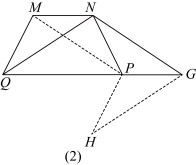
(2)如图(2)所示,已知梯形![]() 中,
中,![]() ,且
,且![]() ,
,![]() .请设计一种方案,用一条或两条直线将梯形
.请设计一种方案,用一条或两条直线将梯形![]() 分割,并使得分割成的几个部分可以通过图形运动拼成与剩余部分不重叠无缝隙的等腰三角形.请写出两腰的线段,以及这两条或一条直线与梯形的交点的位置.(模仿(1)中的论述语言:
分割,并使得分割成的几个部分可以通过图形运动拼成与剩余部分不重叠无缝隙的等腰三角形.请写出两腰的线段,以及这两条或一条直线与梯形的交点的位置.(模仿(1)中的论述语言:![]() 为边
为边![]() 中点,
中点,![]() 是梯形
是梯形![]() 的顶点).
的顶点).
23.如图,已知![]() ,
,![]() 为
为![]() 中的两弦,联结
中的两弦,联结![]() ,
,![]() 交弦
交弦![]() 于点
于点![]() ,
,![]() ,且
,且![]() .
.
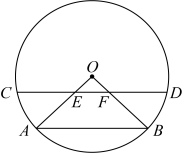
(1)求证:![]() ;
;
(2)如果![]() ,求证:
,求证:![]() .
.
24.在平面直角坐标系中,抛物线![]() 过
过![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)求![]() ,
,![]() 的值.
的值.
(2)设抛物线![]() 过点
过点![]() ,
,![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
①求![]() 的值;
的值;
②当四边形![]() 是直角梯形时,求该直角梯形中最小内角的正弦值.
是直角梯形时,求该直角梯形中最小内角的正弦值.
25.在平行四边形![]() 中,
中,![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 上两点.
上两点.
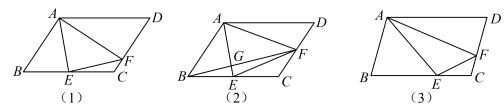
(1)当![]() 是边
是边![]() 中点时,
中点时,
①如图(1),联结![]() ,如果
,如果![]() ,求证:
,求证:![]() ;
;
②如图(2),如果![]() ,联结
,联结![]() ,
,![]() 交边
交边![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
(2)如图(3)所示,联结![]() ,
,![]() ,如果
,如果![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的长.
的长.
参考答案
1.A
2.B
3.D
4.D
5.C
6.B
7.![]()
8.![]()
9.![]()
10.![]() (答案不唯一)
(答案不唯一)
11.![]()
12.![]()
13.![]()
14.![]()
15.1800人
16.![]()
17.![]() ##
##![]()
18.![]() 或
或![]()
19.![]()
20.![]()
21.(1)![]()
(2)![]()
22.(1)![]()
(2)见解析
【详解】
(2)解:如图(2),连接![]() ,把
,把![]() 沿
沿![]() 平移使M与P对应,得到
平移使M与P对应,得到![]() ;再把
;再把![]() 沿
沿![]() 对折,得到
对折,得到![]() ,H与N是对应点,则
,H与N是对应点,则![]() 是等腰三角形,其中两腰分别为
是等腰三角形,其中两腰分别为![]() ,点N、Q分别是梯形的顶点.
,点N、Q分别是梯形的顶点.
23.
【详解】(1)证明:如图所示,连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

(2)证明:如图所示,连接![]() ,
,
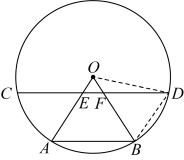
∵![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
由(1)可得![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
24.(1)![]()
(2)①3;②![]() 或
或![]() .
.
25.(1)①见解析;②![]()
(2)![]()
