2025年安徽中考数学真题及答案
一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的．
1．在-2，0，2，5这四个数中，最小的数是（ ）
A．-2B．0C．2D．5
2．安徽省2025年第一季度工业用电量为521.7亿千瓦时，其中521.7亿用科学记数法表示为（ ）
A．
B．
C．
D．
3．“阳马”是由长方体截得的一种几何体，如图水平放置的“阳马”的主视图为（ ）
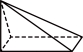
A．
B．
C．
D．
4．下列计算正确的是（ ）
A．
B．
C．
D．
5．下列方程中，有两个不相等的实数根的是（ ）
A．
B．
C．
D．
6．如图，在
中，
，
，边
的中点为D，边
上的点E满足
．若
，则
的长是（ ）
A．
B．6C．
D．3
7．已知一次函数
的图象经过点M
，且y随x的增大而增大．若点N在该函数的图象上，则点N的坐标可以是（ ）
A．
B．
C．
D．
8．在如图所示的
中，
，
分别为边
，
的中点，点
，
分别在边
，
上移动（不与端点重合），且满足
，则下列为定值的是（ ）
A．四边形
的周长B．
的大小
C．四边形
的面积D．线段
的长
9．已知二次函数
的图象如图所示，则（ ）
A．
B．
C．
D．
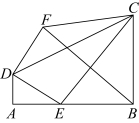
10．如图，在四边形
中，
，
，
，
，点
为边
上的动点．将线段
绕点
逆时针旋转
得到线段
，连接
，
，
，则下列结论错误的是（ ）
A．
的最大值是
B．
的最小值是
C．
的最小值是
D．
的最大值是
二、填空题（本大题共4小题，每小题5分，满分20分）
11．计算：
．
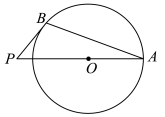
12．如图，
是
的弦，
与
相切于点B，圆心O在线段
上．已知
，则
的大小为 
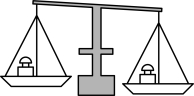
13．在一个平衡的天平左、右两端托盘上，分别放置质量为
和
的物品后，天平倾斜（如图所示）．现从质量为
，
，
，
的四件物品中，随机选取两件放置在天平的左端托盘上，则天平恢复平衡的概率为 ．
14．对于正整数n，根据n除以3的余数，分以下三种情况得到另一个正整数m：若余数为0．则
；若余数为1，则
；若余数为2，则
．这种得到m的过程称为对n进行一次“变换”．对所得的数m再进行一次变换称为对n进行二次变换，依此类推．例如，正整数
，根据4除以3的余数为1，由
知，对4进行一次变换得到的数为8；根据8除以3的余数为2，由
知，对4进行二次变换得到的数为9；根据9除以3的余数为0，由
知，对4进行三次变换得到的数为3．
（1）对正整数15进行三次变换，得到的数为 ；
（2）若对正整数n进行二次变换得到的数为1，则所有满足条件的n的值之和为 ．
三、（本大题共2小题，每小题8分，满分16分）
15．先化简，再求值：
，其中
．
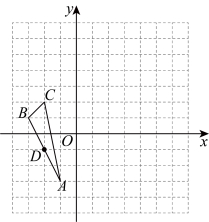
16．如图，在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系
，
的顶点和
均为格点（网格线的交点）．已知点A和
的坐标分别为
和
(1)在所给的网格图中描出边
的中点D，并写出点D的坐标；
(2)以点O为位似中心，将
放大得到
，使得点A的对应点为
，请在所给的网格图中画出
．
四、（本大题共2小题，每小题8分，满分16分）
17．某公司为庆祝新产品上市，在甲楼与乙楼的楼顶之间悬挂彩带营造喜庆气氛．如图所示，甲楼和乙楼分别用与水平地面垂直的线段
和
表示，彩带用线段
表示．工作人员在点A处测得点C的俯角为
，测得点D的仰角为
．已知
，求
的长（精确到
）．参考数据：
，
，
，
，
，
．
18．如图，在平面直角坐标系
中，一次函数
与反比例函数
的图象交于A，B两点．已知点A和B的横坐标分别为6和2．
(1)求a与k的值；
(2)设直线
与x轴、y轴的交点分别为C，D，求
的面积．
五、（本大题共2小题，每小题10分，满分20分）
19．某景区管理处为了解景区的服务质量，现从该景区
月份的游客中随机抽取
人对景区的服务质量进行评分，评分结果用
表示（单位：分），将全部评分结果按以下五组进行整理，并绘制统计表，部分信息如下：
组别 | | | | | |
分组 | | | | | |
人数 | | | | | |
请根据以上信息，完成下列问题：
(1)
________；
(2)这
名游客对该景区服务质量评分的中位数落在________组；
(3)若游客评分的平均数不低于
，则认定该景区的服务质量良好．分别用
，
，
，
，
作为
，
，
，
，
这五组评分的平均数，估计该景区
月份的服务质量是否良好，并说明理由．
20．如图，四边形
的顶点都在半圆O上，
是半圆O的直径，连接
，
．
(1)求证：
；
(2)若
，
，求
的长．
六、（本题满分12分）
21．综合与实践
【项目主题】
某劳动实践小组拟用正三角形和正六边形两种环保组件改善小区幼儿园室内活动场地．
【项目准备】
（1）密铺知识学习：用形状、大小完全相同的一种或几种平面图形进行拼接，使图形之间既没有空隙也没有重叠地铺成一片，叫做图形的密铺
（2）密铺方式构建：运用密铺知识得到图1、图2所示的两种拼接方式，其中正六边形和正三角形组件的边长均为
．
（3）密铺规律探究：为方便研究，称图3、图4分别为图1、图2的“拼接单元”．
观察发现：自左向右拼接图1时，每增加一个图3所示的拼接单元，则增加1个正六边形和2个正三角形，长度增加
，从而x个这样的拼接单元拼成一行的长度为
．
自左向右拼接图2时，每增加一个图4所示的拼接单元，则增加① 个正六边形和② 个正三角形，长度增加③ cm，从而y个这样的拼接单元拼成一行的长度为④ cm．
【项目分析】
（1）项目条件：场地为长
、宽
的矩形；正三角形和正六边形组件的单价分别为1元和5元．
（2）基本约定：项目成本仅计算所需组件的费用．
（3）方式确定：
（i）考虑成本因素，采用图1方式进行密铺；
（ii）每行用正六边形组件顶着左墙开始，从左向右用一个正六边形与两个正三角形组件按图1所示方式依次交替拼接，当不能继续拼接时，该行拼接结束；
（iii）第一行紧靠墙边，从前往后按相同方式逐行密铺，直至不能拼接为止．
（4）方案论证：按上述确定的方式进行密铺，有以下两种方案．
方案一：第一行沿着长度为6 m的墙自左向右拼接（如图5）．
根据规律，令
，解得
，所以每行可以先拼
块拼接单元，即共用去
个正六边形和
个正三角形组件，由
知，所拼长度为
，剩余
恰好还可以摆放一个正六边形组件（如图5所示的阴影正六边形）．最终需用
个正六边形和
个正三角形组件，由
知，方案一每行的成本为
元．
由于每行宽度为
（按
计算），设拼成s行，则
，解得
，故需铺
行．由
知，方案一所需的总成本为
元．
方案二：第一行沿着长度为
的墙自左向右拼接．
类似于方案一的成本计算，令
方案二每行的成本为⑤ 元，总成本为⑥ 元．
【项目实施】
根据以上分析，选用总成本较少的方案完成实践活动（略）．
请将上述材料中横线上所缺内容补充完整：
________；②________；③________；④________；⑤________；⑥________．
七、（本题满分12分）
22．已知点
在正方形
内，点E在边
上，
是线段
的垂直平分线，连接
，
．
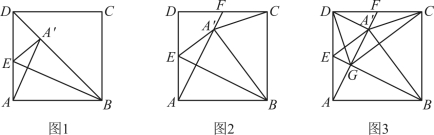
(1)如图1，若
的延长线经过点D，
，求
的长；
(2)如图2，点F是
的延长线与
的交点，连接
．
①求证：
；
②如图3，设
，
相交于点G，连接
，
，
．若
，判断
的形状，并说明理由．
八、（本题满分14分）
23．已知抛物线
经过点
．
(1)求该抛物线的对称轴；
(2)点
和
分别在抛物线
和
上（
与原点都不重合）．
①若
，且
，比较
与
的大小；
②当
时，若
是一个与
无关的定值，求
与
的值
参考答案
1．A
2．C
3．A
4．B
5．D
6．B
7．D
8．C
9．C
10．A
11．6
12．20
13．
14． 2 11
15．
，1
16．(1)图见解析；
(2)图见解析
【详解】（1）解：如图所示，点D即为边
的中点，
∵
，
∴点D的坐标为
．
（2）解：如图所示，
即为所求作的三角形．
17．
18．(1)
，
(2)16
19．(1)
；
(2)D；
(3)该景区
月份的服务质量良好，理由见解析．
20．(1)详见解析
(2)6
【详解】（1）证明：∵
，
，
∴
，
∴
．
21．
；
；
；
；
；
22．(1)
(2)
详见解析；
为等腰直角三角形
【详解】
（2）解：①证明：由题意知，
，
∴
，
．
∴
，
∴
．
23．(1)对称轴是直线
(2)
；
，