2024年安徽中考数学试题及答案
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1. ﹣5的绝对值是( )
A. 5 B. ﹣5 C. ![]() D.
D. ![]()
2. 据统计,![]() 年我国新能源汽车产量超过
年我国新能源汽车产量超过![]() 万辆,其中
万辆,其中![]() 万用科学记数法表示为( )
万用科学记数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 某几何体的三视图如图所示,则该几何体为( )
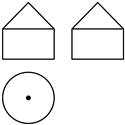
A. 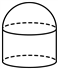 B.
B. 
C. 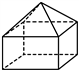 D.
D. 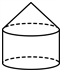
4. 下列计算正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
5. 若扇形![]() 的半径为6,
的半径为6,![]() ,则
,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 已知反比例函数![]() 与一次函数
与一次函数![]() 的图象的一个交点的横坐标为3,则k的值为( )
的图象的一个交点的横坐标为3,则k的值为( )
A. ![]() B.
B. ![]() C. 1 D. 3
C. 1 D. 3
7. 如图,在的延长线上,且![]() ,则
,则![]() 的长是( )
的长是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 已知实数a,b满足![]() ,
,![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
9. 在凸五边形的中点.下列条件中,不能推出![]() 与
与![]() 一定垂直的是( )
一定垂直的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
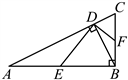
10. 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上的高.点E,F分别在边
上的高.点E,F分别在边![]() ,
,![]() 上(不与端点重合),且
上(不与端点重合),且![]() .设
.设![]() ,四边形
,四边形![]() 的面积为y,则y关于x的函数图象为( )
的面积为y,则y关于x的函数图象为( )
A. 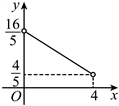 B.
B. 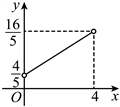
C.  D.
D. 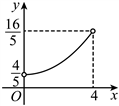
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 若代数式![]() 有意义,则实数
有意义,则实数![]() 的取值范围是_____
的取值范围是_____
12. 我国古代数学家张衡将圆周率取值为![]() ,祖冲之给出圆周率的一种分数形式的近似值为
,祖冲之给出圆周率的一种分数形式的近似值为![]() .比较大小:
.比较大小:![]() ______
______![]() (填“>”或“<”).
(填“>”或“<”).
13. 不透明的袋中装有大小质地完全相同的![]() 个球,其中
个球,其中![]() 个黄球、
个黄球、![]() 个白球和
个白球和![]() 个红球.从袋中任取
个红球.从袋中任取![]() 个球,恰为
个球,恰为![]() 个红球的概率是______.
个红球的概率是______.
14. 如图,现有正方形纸片![]() ,点E,F分别在边
,点E,F分别在边![]() 上,沿垂直于
上,沿垂直于![]() 的直线折叠得到折痕
的直线折叠得到折痕![]() ,点B,C分别落在正方形所在平面内的点
,点B,C分别落在正方形所在平面内的点![]() ,
,![]() 处,然后还原.
处,然后还原.

(1)若点N在边![]() 上,且
上,且![]() ,则
,则![]() ______(用含α的式子表示);
______(用含α的式子表示);
(2)再沿垂直于![]() 的直线折叠得到折痕
的直线折叠得到折痕![]() ,点G,H分别在边
,点G,H分别在边![]() 上,点D落在正方形所在平面内的点
上,点D落在正方形所在平面内的点![]() 处,然后还原.若点
处,然后还原.若点![]() 在线段
在线段![]() 上,且四边形
上,且四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() 与
与![]() 的交点为P,则
的交点为P,则![]() 的长为______.
的长为______.
三、(本大题共2小题,每小题8分,满分16分)
15. 解方程:![]()
16. 如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系![]() ,格点(网格线的交点)A、B,C、D的坐标分别为
,格点(网格线的交点)A、B,C、D的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
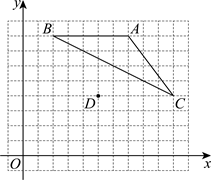
(1)以点D为旋转中心,将![]() 旋转
旋转![]() 得到
得到![]() ,画出
,画出![]() ;
;
(2)直接写出以B,![]() ,
,![]() ,C为顶点的四边形的面积;
,C为顶点的四边形的面积;
(3)在所给的网格图中确定一个格点E,使得射线![]() 平分
平分![]() ,写出点E的坐标
,写出点E的坐标
四、(本大题共2小题,每小题8分,满分16分)
17. 乡村振兴战略实施以来,很多外出人员返乡创业.某村有部分返乡青年承包了一些田地.采用新技术种植![]() 两种农作物.种植这两种农作物每公顷所需人数和投入资金如表:
两种农作物.种植这两种农作物每公顷所需人数和投入资金如表:
农作物品种 | 每公顷所需人数 | 每公顷所需投入资金(万元) |
|
|
|
|
|
|
已知农作物种植人员共![]() 位,且每人只参与一种农作物种植,投入资金共
位,且每人只参与一种农作物种植,投入资金共![]() 万元.问
万元.问![]() 这两种农作物的种植面积各多少公顷?
这两种农作物的种植面积各多少公顷?
18. 数学兴趣小组开展探究活动,研究了“正整数N能否表示为![]() (
(![]() 均为自然数)”的问题.
均为自然数)”的问题.
(1)指导教师将学生的发现进行整理,部分信息如下(![]() 为正整数):
为正整数):
| 奇数 |
|
表示结果 |
|
|
|
| |
|
| |
|
| |
|
| |
|
| |
一般结论 | |
|
按上表规律,完成下列问题:
(![]() )
)![]() ( )
( )![]() ( )
( )![]() ;
;
(![]() )
)![]() ______;
______;
(2)兴趣小组还猜测:像![]() 这些形如
这些形如![]() (
(![]() 为正整数)的正整数
为正整数)的正整数![]() 不能表示为
不能表示为![]() (
(![]() 均为自然数).师生一起研讨,分析过程如下:
均为自然数).师生一起研讨,分析过程如下:
假设 分下列三种情形分析:
则 而
则 而
而 由 |
阅读以上内容,请在情形![]() 的横线上填写所缺内容
的横线上填写所缺内容
五、(本大题共2小题,每小题10分,满分20分)
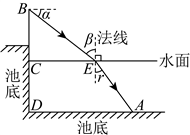
19. 科技社团选择学校游泳池进行一次光的折射实验,如图,光线自点![]() 处发出,经水面点
处发出,经水面点![]() 折射到池底点
折射到池底点![]() 处.已知
处.已知![]() 与水平线的夹角
与水平线的夹角![]() ,点
,点![]() 到水面的距离
到水面的距离![]() m,点
m,点![]() 处水深为
处水深为![]() ,到池壁的水平距离
,到池壁的水平距离![]() ,点
,点![]() 在同一条竖直线上,所有点都在同一竖直平面内.记入射角为
在同一条竖直线上,所有点都在同一竖直平面内.记入射角为![]() ,折射角为
,折射角为![]() ,求
,求![]() 的值(精确到
的值(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ).
).
20. 如图,![]() 是
是![]() 的外接圆,D是直径
的外接圆,D是直径![]() 上一点,
上一点,![]() 的平分线交
的平分线交![]() 于点E,交
于点E,交![]() 于另一点F,
于另一点F,![]() .
.

(1)求证:![]() ;
;
(2)设![]() ,垂足为M,若
,垂足为M,若![]() ,求
,求![]() 的长.
的长.
六、(本题满分12分)
21. 综合与实践
【项目背景】
无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
【数据收集与整理】
从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:![]() )表示.
)表示.
将所收集的样本数据进行如下分组:
组别 | A | B | C | D | E |
x |
|
|
|
|
|
整理样本数据,并绘制甲、乙两园样本数据的频数直方图,部分信息如下:

任务1 求图1中a的值.
【数据分析与运用】
任务2 A,B,C,D,E五组数据的平均数分别取为4,5,6,7,8,计算乙园样本数据的平均数.
任务3 下列结论一定正确的是______(填正确结论的序号).
①两园样本数据的中位数均在C组;
②两园样本数据的众数均在C组;
③两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将C,D两组的柑橘认定为一级,B组的柑橘认定为二级,其它组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务
七、(本题满分12分)
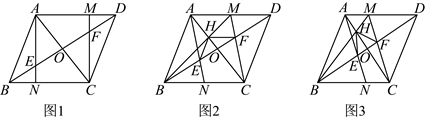
22. 如图1,![]() 的对角线
的对角线![]() 与
与![]() 交于点O,点M,N分别在边
交于点O,点M,N分别在边![]() ,
,![]() 上,且
上,且![]() .点E,F分别是
.点E,F分别是![]() 与
与![]() ,
,![]() 的交点.
的交点.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于点H,连接
于点H,连接![]() ,
,![]() .
.
(ⅰ)如图2,若![]() ,求证:
,求证:![]() ;
;
(ⅱ)如图3,若![]() 为菱形,且
为菱形,且![]() ,
,![]() ,求
,求![]() 的值.
的值.
八、(本题满分14分)
23. 已知抛物线![]() (b为常数)的顶点横坐标比抛物线
(b为常数)的顶点横坐标比抛物线![]() 的顶点横坐标大1.
的顶点横坐标大1.
(1)求b的值;
(2)点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在抛物线
在抛物线![]() 上.
上.
(ⅰ)若![]() ,且
,且![]() ,
,![]() ,求h的值;
,求h的值;
(ⅱ)若![]() ,求h的最大值
,求h的最大值
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
【1题答案】
【答案】A
【2题答案】
【答案】B
【3题答案】
【答案】D
【4题答案】
【答案】C
【5题答案】
【答案】C
【6题答案】
【答案】A
【7题答案】
【答案】B
【8题答案】
【答案】C
【9题答案】
【答案】D
【10题答案】
【答案】A
二、填空题(本大题共4小题,每小题5分,满分20分)
【11题答案】
【答案】![]()
【12题答案】
【答案】>
【13题答案】
【答案】![]()
【14题答案】
【答案】 ①. ![]() ##
##![]() ②.
②. ![]()
三、(本大题共2小题,每小题8分,满分16分)
【15题答案】
【答案】![]() ,
,![]()
【16题答案】
【答案】(1)见详解 (2)40
(3)![]() (答案不唯一)
(答案不唯一)
四、(本大题共2小题,每小题8分,满分16分)
【17题答案】
【答案】![]() 农作物的种植面积为
农作物的种植面积为![]() 公顷,
公顷,![]() 农作物的种植面积为
农作物的种植面积为![]() 公顷.
公顷.
【18题答案】
【答案】(1)(![]() )
)![]() ,
,![]() ;(
;(![]() )
)![]() ;
;
(2)![]()
五、(本大题共2小题,每小题10分,满分20分)
【19题答案】
【答案】![]()
【20题答案】
【答案】(1)见详解 (2)![]() .
.
六、(本题满分12分)
【21题答案】
【答案】任务1:40;任务2:6;任务3:①;任务4:乙园的柑橘品质更优,理由见解析
七、(本题满分12分)
【22题答案】
【答案】(1)见详解 (2)(ⅰ)见详解,(ⅱ)![]()
八、(本题满分14分)
【23题答案】
【答案】(1)![]()
(2)(ⅰ)3;(ⅱ)![]()
