2025年云南中考数学试题及答案
一、选择题:本题共15小题,每小题2分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.中国是最早使用正负数表示具有相反意义的量的国家.若收入10元记作![]() 元,则支出5元可记作( )
元,则支出5元可记作( )
A.![]() 元B.5元C.
元B.5元C.![]() 元D.10元
元D.10元
2.地球绕太阳公转的速度约是![]() ,110000用科学记数法可以表示为( )
,110000用科学记数法可以表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
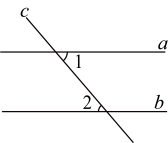
3.如图,已知直线![]() 与直线
与直线![]() 都相交.若
都相交.若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列计算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若点![]() 在反比例函数
在反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象上,则
)的图象上,则![]() ( )
( )
A.1B.2C.3D.4
6.下列图形是某几何体的三视图(主视图也称正视图,左视图也称侧视图),则这个几何体是( )
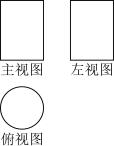
A.正方体B.长方体C.圆锥D.圆柱
7.一个六边形的内角和等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
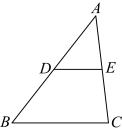
8.如图,在![]() 中,已知
中,已知![]() 分别是
分别是![]() 边上的点,且
边上的点,且![]() .若
.若![]() ,则
,则![]() ()
()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 的自变量
的自变量![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.中华文明,源远流长;中华汉字,寓意深广,下列四个选项中,是轴对称图形的为( )
A. B.
B. C.
C. D.
D.
11.某校举办了关于垃圾分类的知识竞赛.九年级10名学生参加本次竞赛的成绩(单位:分)分别为90,80,90,70,90,100,80,90,90,80.这组数据的众数是( )
A.70B.80C.90D.100
12.按一定规律排列的代数式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,第
,…,第![]() 个代数式是( )
个代数式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.若一个圆锥的侧面展开图的圆心角度数为![]() ,母线长为
,母线长为![]() ,则该圆锥的底面圆的半径为( )
,则该圆锥的底面圆的半径为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.某书店今年3月份盈利6000元,5月份盈利6200元.设该书店每月盈利的平均增长率为![]() ,根据题意,下列方程正确的是( )
,根据题意,下列方程正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
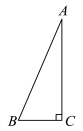
15.如图,在![]() 中,
中,![]() .若
.若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本题共4小题,每小题2分,共8分.
16.已知![]() 的半径为
的半径为![]() ,若点
,若点![]() 在
在![]() 上,则点
上,则点![]() 到圆心
到圆心![]() 的距离为
的距离为 ![]() .
.
17.分解因式:![]() = .
= .
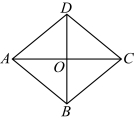
18.如图,四边形![]() 是菱形,对角线
是菱形,对角线![]() 相交于点
相交于点![]() .若
.若![]() ,
,![]() ,则菱形
,则菱形![]() 的面积是 .
的面积是 .
19.某中学为了解全校![]() 名学生对新闻,娱乐,体育,动画,戏曲五类电视节目的喜爱情况,学校就“我最喜爱的电视节目”作了一次简单随机抽样调查.如图是根据调查结果绘制的扇形统计图.根据图中的信息,该校
名学生对新闻,娱乐,体育,动画,戏曲五类电视节目的喜爱情况,学校就“我最喜爱的电视节目”作了一次简单随机抽样调查.如图是根据调查结果绘制的扇形统计图.根据图中的信息,该校![]() 名学生中,最喜爱娱乐节目的学生大约有 名.
名学生中,最喜爱娱乐节目的学生大约有 名.

三、解答题:本题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤.
20.计算:![]() .
.
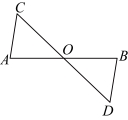
21.如图,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() .求证:
.求证:![]() .
.
22.某化工厂采用机器人![]() ,机器人
,机器人![]() 搬运化工原料,机器人
搬运化工原料,机器人![]() 比机器人
比机器人![]() 每小时少搬运20千克,机器人
每小时少搬运20千克,机器人![]() 搬运800千克所用时间与机器人
搬运800千克所用时间与机器人![]() 搬运1000千克所用时间相等.求机器人
搬运1000千克所用时间相等.求机器人![]() ,机器人
,机器人![]() 每小时分别搬运多少千克化工原料.
每小时分别搬运多少千克化工原料.
23.九年级某班学生计划到甲,乙两个敬老院开展献爱心活动,老师把该班学生分成![]() 两个小组,通过游戏方式确定去哪个敬老院.游戏规则如下:在一个不透明的箱子中放了分别标有数字1,2的两张卡片(除数字外,都相同),班长先从这个箱子里任意摸出一张卡片,卡片上的数字记为
两个小组,通过游戏方式确定去哪个敬老院.游戏规则如下:在一个不透明的箱子中放了分别标有数字1,2的两张卡片(除数字外,都相同),班长先从这个箱子里任意摸出一张卡片,卡片上的数字记为![]() .在另一个不透明的箱子中放了分别标有数字1,2,3的三张卡片(除数字外,都相同),班长再从该箱子里任意摸出一张卡片,卡片上的数字记为
.在另一个不透明的箱子中放了分别标有数字1,2,3的三张卡片(除数字外,都相同),班长再从该箱子里任意摸出一张卡片,卡片上的数字记为![]() .若
.若![]() ,则
,则![]() 组学生到甲敬老院,
组学生到甲敬老院,![]() 组学生到乙敬老院;若
组学生到乙敬老院;若![]() ,则
,则![]() 组学生到乙敬老院,
组学生到乙敬老院,![]() 组学生到甲敬老院.
组学生到甲敬老院.
(1)用列表法或画树状图法中的一种方法,求![]() 所有可能出现的结果总数;
所有可能出现的结果总数;
(2)求![]() 组学生到甲敬老院,
组学生到甲敬老院,![]() 组学生到乙敬老院开展献爱心活动的概率
组学生到乙敬老院开展献爱心活动的概率![]() .
.
24.如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点.延长
的中点.延长![]() 至点
至点![]() ,使
,使![]() .连接
.连接![]() ,记
,记![]() ,
,![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,四边形
,四边形![]() 的周长为
的周长为![]() .
.
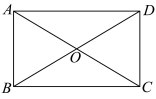
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,求
,求![]() 的长.
的长.
25.请你根据下列素材,完成有关任务.
背景 | 某校计划购买篮球和排球,供更多学生参加体育锻炼,增强身体素质. |
素材一 | 购买 |
素材二 | 购买 |
素材三 | 该校计划购买篮球和排球共 |
请完成下列任务: | |
任务一 | 每个篮球,每个排球的价格分别是多少元? |
任务二 | 给出最节省费用的购买方案. |
26.已知![]() 是常数,函数
是常数,函数![]() ,记
,记![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
27.如图,![]() 是五边形
是五边形![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径.连接
的直径.连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)若![]() ,且
,且![]() ,求
,求![]() 的度数;
的度数;
(2)求证:直线![]() 是
是![]() 的切线;
的切线;
(3)探究,发现与证明:已知![]() 平分
平分![]() ,是否存在常数
,是否存在常数![]() ,使等式
,使等式![]() 成立?若存在,请直接写出一个
成立?若存在,请直接写出一个![]() 的值和一个
的值和一个![]() 的值,并证明你写出的
的值,并证明你写出的![]() 的值和
的值和![]() 的值,使等式
的值,使等式![]() 成立;若不存在,请说明理由.
成立;若不存在,请说明理由.
参考答案
1.A
2.C
3.D
4.B
5.B
6.D
7.C
8.A
9.D
10.C
11.C
12.A
13.B
14.A
15.D
16.![]()
17.![]()
18.![]()
19.![]()
20.8
21.证明见解析
【详解】证明;在![]() 和
和![]() 中,
中,
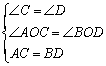 ,
,
∴![]() .
.
22.机器人A每小时搬运80千克化工原料,机器人B每小时搬运100千克化工原料
23.
(1)![]()
(2)![]()
24.
(1)见解析
(2)10
【详解】(1)证明:∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴四边形![]() 是矩形;
是矩形;
25.
任务一:每个篮球![]() 元,每个排球
元,每个排球![]() 元;任务二:购买篮球
元;任务二:购买篮球![]() 个,排球
个,排球![]() 个,最节省费用.
个,最节省费用.
26.
(1)![]() 的值为
的值为![]() ;
;
(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
27.
(1)![]() ;
;
(2)证明见解析;
(3)存在常数![]() ,
,![]() ,理由见解析.
,理由见解析.
【详解】(1)解:∵![]() ,且
,且![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ;
;
(2)解:如图,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
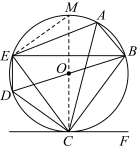
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的半径,
的半径,
∴直线![]() 是
是![]() 的切线;
的切线;
(3)解:存在常数![]() ,
,![]() ,使等式
,使等式![]() 成立;
成立;
理由如下:
如图,设![]() 与
与![]() 交于点
交于点![]() ,
,

∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() 得:
得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
