2025年四川达州中考数学试题及答案
第I卷（选择题共40分）
一、单项选择题（每小题4分，共40分）
1．如果收入100元记作
元，那么支出40元应记作（ ）
A．
元B．
元C．
元D．
元
2．下图是大竹“东汉醪糟”包装盒组成的立体图形，其主视图为（ ）
A．
B．
C．
D．
3．“悟空”号全海深
是中国哈尔滨工程大学自主研发的无人无缆潜水器，具备在
米深海自主作业的能力，数据
用科学记数法表示为（ ）
A．
B．
C．
D．
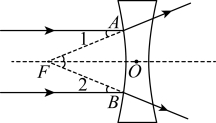
4．如图，一束平行于主光轴的光线经过凹透镜后，其折射光线的反向延长线交于主光轴的焦点F．若
，则
的度数为（ ）
A．
B．
C．
D．
5．下列各式运算结果为
的是（ ）
A．
B．
C．
D．
6．小明随机抽查爱民小区6户家庭月均用水情况，分别是：3，4，5，7，6，5（单位：
），关于这组数据，下列说法正确的是（ ）
A．众数是5B．中位数是6C．平均数是6D．极差是3
7．《九章算术》中记载了这样一道题：牛5头和羊2只共值10金，牛2头和羊5只共值8金，问牛和羊各值多少金？设每头牛值x金，每只羊值y金，可列方程组为（ ）
A．
B．
C．
D．
8．下列说法正确的是（ ）
A．两点之间线段最短
B．平行四边形是轴对称图形
C．若
有意义，则x的取值范围是全体实数
D．三角形的中位线将三角形分成面积相等的两部分
9．如图，在
中，
，线段
的垂直平分线交
于点E，交
于点D，则
的周长为（ ）
A．21B．14C．13D．9
10．如图，抛物线
与x轴交于点
，点
，下列结论：①
；②
；③
；④
．正确的个数为（ ）
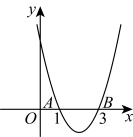
A．1个B．2个C．3个D．4个
第II卷（非选择题共110分）
二、填空题（每小题4分，共20分）
11．因式分解：
．
12．已知关于
的方程
的一个根是
，则
的值为 ．
13．如图，圆锥的侧面展开图是一个扇形，已知圆锥的底面半径为2，则扇形的弧长是 ．
14．化简：
．
15．定义：在平面直角坐标系中，一个图形向右平移a个单位长度，再绕原点按顺时针方向旋转
角度，这样的图形运动叫做图形的
变换，现将斜边为1的等腰直角三角形
放置在如图的平面直角坐标系中，
经
变换后得
为第一次变换，
经
变换得
为第二次变换，…，经
变换得
，则点
的坐标是 ．
三、解答题：解答时应写出必要的文字说明、证明过程或演算步骤（共90分）
16．（1）计算：
；
（2）解不等式：
并把解集表示在数轴上．
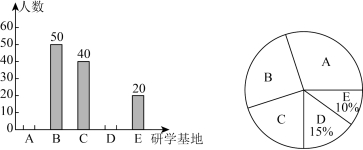
17．项目调研
项目主题 | 阳光学校学生研学需求情况调查 |
调查人员 | 数学兴趣小组 |
调查方法 | 抽样调查 |
调研内容 | 阳光学校计划组织学生前往以下5个研学基地中的一个基地进行研学，5个研学基地分别为：A．张爱萍故居；B．王维舟纪念馆；C．万源保卫战纪念馆；D．广子村农业示范园；E．开江白宝塔． 数学兴趣小组对本校学生的意向目的地展开抽样调查，并为学校出具了调查报告（每位学生只能选1个研学基地） |
统计数据 | |
请阅读上述材料，解决下列问题：
(1)请将条形统计图补充完整，意向参加B研学基地人数对应的扇形圆心角度数是_______；
(2)若该校共有2000名学生，请你估计全校参加A研学基地的学生人数；
(3)甲同学从B，C，D三个基地中随机选择一个参加研学，乙同学从C，D两个基地中随机选择一个参加研学，请用列表或画树状图的方法，求两位同学选择相同研学基地的概率．
18．开启作角平分线的智慧之窗
问题：作
的平分线
作法：甲同学用尺规作出了角平分线；乙同学用圆规和直角三角板作出了角平分线；丙同学也用尺规作出了角平分线，工人师傅用带刻度的直角弯尺，通过移动弯尺使上下相同刻度在角的两边上．即得
为
的平分线；
讨论：大家对甲同学和工人师傅的作法都深信不疑．认为判断角平分线的依据是利用三角形全等，其判定全等的方法是_______；
对乙同学作法半信半疑，通过讨论最终确定的判定依据：①三角形全等，
，
或
，②_______________；
对丙同学的作法陷入了沉思．
任务：
(1)请你将上述讨论得出的依据补充完整；
(2)完成对丙同学作法的验证．
已知
，求证：
平分
．
19．如图，直线
与双曲线
交于点
，点
．
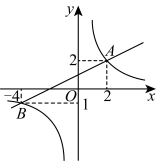
(1)求一次函数与反比例函数的表达式；
(2)点P在x轴上，
，求点P的坐标．
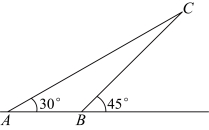
20．为了让莲花湖湿地公园的天更蓝，水更清，莲花湖管委会定期利用无人机指引工作人员清理湖中垃圾．已知无人机悬停在湖面上的
处，工作人员所乘小船在
处测得无人机的仰角为
，当工作人员沿正前方向划行
米到达
处，测得无人机的仰角为
，求无人机离湖面的高度（结果不取近似值）
21．归纳与应用
归纳是学好数学的敲门砖，尤其对几何而言．例如，我们看到图1是平行四边形，就会联想到：从边的角度，平行四边形对边平行且相等；从角的角度，平行四边形对角相等，邻角互补；从对角线的角度，平行四边形对角线互相平分；从对称性的角度，平行四边形是中心对称图形通过如此归纳形成知识体系的学习方法，成为我们解决相关问题的金钥匙：
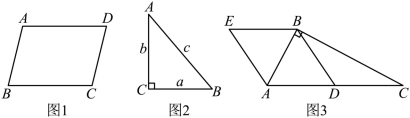
(1)尝试归纳：请你根据图2，写出3条直角三角形的性质
①____________________________________________________________________________；
②____________________________________________________________________________；
③____________________________________________________________________________．
(2)实践应用：小明同学在思考直角三角形的性质时，作出如图3，
，点D是
的中点，
，
，试帮他判断四边形
的形状，并证明你的结论．
22．为弘扬达州地方文化，让更多游客了解巴人故里，某文旅公司推出多款文创产品．已知某款巴小虎吉祥物的成本价是30元，当售价为40元时，每天可以售出60件，经调查发现，售价每降价1元，每天可以多售出10件．
(1)设该款巴小虎吉祥物降价x元，则每天售出的数量是_______件；
(2)为让利于游客，该款巴小虎吉祥物应该降价多少元，文旅公司每天的利润是630元；
(3)文旅公司每天售卖该款巴小虎吉祥物的利润为W元，当售价为多少元时，每天的利润最大？最大利润是多少？
23．如图，在
中，
是弦，
是
的切线，
，点
，
，
分别是线段
，
，
上的动点，连接
，
，
(1)试判断
与
的位置关系，并说明理由；
(2)若
，试求
与
半径
的数量关系．
24．如图，已知抛物线
交x轴于A，B两点，交y轴于C点，B的坐标为
，C的坐标为
，顶点为M．
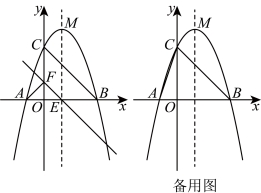
(1)求抛物线的解析式；
(2)连接
，过第四象限内抛物线上一点作
的平行线，交x轴于点E，交y轴于点F．
①连接
，当
时，求
内切圆半径r与外接圆半径R的比值；
②连接
，当点F在
的内角平分线上，
上的动点P满足
的值最小时，求
的面积．
25．综合与实践
问题提出：探究图形中线段之间的数量关系，通常将一个图形分割成几个图形，根据面积不变，获得线段之间的数量关系
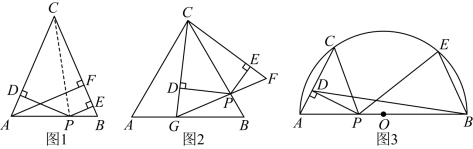
探究发现：如图1，在
中，
，
是
边上一点，过点
作
于
，
于
，过点
作
于
．连结
，由图形面积分割法得：
______；则
______
______．
实践应用：如图2，
是等边三角形，
，点
是
边上一点，连结
．将线段
绕点
逆时针旋转
得
，连结
交
于
，过点
作
于
，
于
，当
时，求
的值．
拓展延伸：如图3，已知
是半圆
的直径，
，
是弦，
，
是
上一点，
，垂足为
，
，求
的值．
参考答案
1．C
2．B
3．B
4．A
5．B
6．A
7．D
8．A
9．C
10．D
11．
12．
13．
14．
15．
16．（1）2；（2）
，数轴见解析
17．(1)
(2)
(3)
18．(1)
；全等三角形的对应角相等
(2)见解析
【详解】
（2）证明：∵
，
∴
，
∴
，
∵
，
∴
，
∴
，
∴
平分
．
19．(1)一次函数解析式为
，反比例函数解析式为
(2)点
的坐标为
或
20．无人机离湖面的高度为
米
21．(1)见解析
(2)四边形
是菱形，见解析
【详解】（1）解：直角三角形的3条性质：
①
；
②
；
③
；
（2）解：四边形
是菱形，理由如下：
∵
，
，
∴四边形
是平行四边形，
∵
，点D是
的中点，
∴
，
∴四边形
是菱形．
22．(1)
(2)3元
(3)售价为38元时，每天的利润最大，最大利润是640元
23．(1)
是
的切线，理由见解析
(2)
【详解】（1）解：
是
的切线，理由如下：
如图，连接
，
∵
，
∴
，
∵
，
∴
，
∵
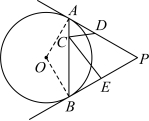
是
的切线，
∴
，
∴
，
又∵
是
的半径，
∴
是
的切线；
24．(1)
(2)①
；②
的面积为2或3或
25．探究发现：
，
；实践应用：
；拓展延伸：