2025年江苏连云港中考数学试题及答案
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项符合题目要求,请将正确选项前的字母代号填涂在答题卡相应位置上)
1. ![]() 的绝对值是( )
的绝对值是( )
A. 5B. ![]() C.
C. ![]() D.
D. ![]()
2. 2020年12月17日,“嫦娥五号”返回器携带月球样品顺利返回地球,我国科学家通过研究证明了月球在![]() 年前仍存在岩浆活动.数据
年前仍存在岩浆活动.数据![]() 用科学记数法表示
用科学记数法表示![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 若![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 下列长度(单位:![]() )的3根小木棒能搭成三角形的是( )
)的3根小木棒能搭成三角形的是( )
A. 1,2,3B. 2,3,4C. 3,5,8D. 4,5,10
5. 如图,在![]() 中,
中,![]() ,
,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 、
、![]() 于点D、E,
于点D、E,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 、
、![]() 于点F、G,则
于点F、G,则![]() 的周长为( )
的周长为( )

A. 5B. 6C. 7D. 8
6. 《九章算术》中有一个问题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”(凫:野鸭.所提问题即“野鸭与大雁从南海和北海同时起飞,经过多少天能够相遇?”)如果设经过![]() 天能够相遇,根据题意,得( )
天能够相遇,根据题意,得( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
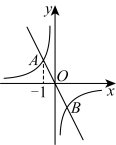
7. 如图,正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于A、B两点,点A的横坐标为
的图像交于A、B两点,点A的横坐标为![]() .当
.当![]() 时,
时,![]() 的取值范围是( )
的取值范围是( )
A. ![]() 或
或![]() B.
B. ![]() 或
或![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
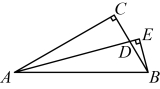
8. 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() ,E为垂足,则
,E为垂足,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共8小题,每小题3分,共24分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)
9. 计算:![]() _______.
_______.
10. 分解因式:![]() _______.
_______.
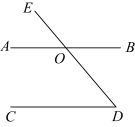
11. 如图,![]() ,直线
,直线![]() 与射线
与射线![]() 相交于点
相交于点![]() .若
.若![]() ,则
,则![]() _______
_______![]() .
.
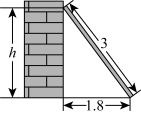
12. 如图,长为![]() 的梯子靠在墙上,梯子的底端离墙脚线的距离为
的梯子靠在墙上,梯子的底端离墙脚线的距离为![]() ,则梯子顶端的高度h为_______m
,则梯子顶端的高度h为_______m
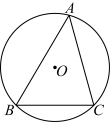
13. 如图,![]() 是
是![]() 的内接三角形,
的内接三角形,![]() .若
.若![]() 的半径为2,则劣弧
的半径为2,则劣弧![]() 的长为_______.
的长为_______.
14. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强![]() 是气球体积
是气球体积![]() 的反比例函数.当
的反比例函数.当![]() 时,
时,![]() .则当
.则当![]() 时,
时,![]() ________Pa.
________Pa.
15. 如图,小亮同学掷铅球时,铅球沿抛物线![]() 运行,其中
运行,其中![]() 是铅球离初始位置的水平距离,
是铅球离初始位置的水平距离,![]() 是铅球离地面的高度.若铅球抛出时离地面的高度
是铅球离地面的高度.若铅球抛出时离地面的高度![]() 为
为![]() ,则铅球掷出的水平距离
,则铅球掷出的水平距离![]() 为________
为________![]() .
.

16. 如图,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点,四边形
上的动点,四边形![]() 为平行四边形,则
为平行四边形,则![]() 的最小值为_______.
的最小值为_______.

三、解答题(本大题共11小题,共102分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤,作图过程需保留作图痕迹)
17![]() 计算
计算![]() .
.
18. 解方程![]() .
.
19. 解不等式组![]()
20. 一只不透明的袋子中装有1个红球和3个白球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,则摸到红球的概率是_______;
(2)搅匀后从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球.用画树状图或列表的方法,求2次都摸到白球的概率.
21. 为了解八年级学生的体重情况,某校随机抽取了八年级部分学生进行测量,收集并整理数据后,绘制了如下尚不完整的统计图表.
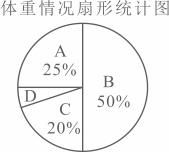
体重情况统计表
组别 | 体重 | 频数(人数) |
| | |
| | |
| | |
| | |
根据以上信息,解答下列问题:
(1)![]() _______,
_______,![]() ________;
________;
(2)在扇形统计图中,![]() 类所对应的圆心角度数是_______°;
类所对应的圆心角度数是_______°;
(3)若该校八年级共有![]() 名学生,估计体重在
名学生,估计体重在![]() 及以上的学生有多少人?
及以上的学生有多少人?
22. 如图,制作甲、乙两种无盖的长方体纸盒,需用正方形和长方形两种硬纸片,且长方形的宽与正方形的边长相等
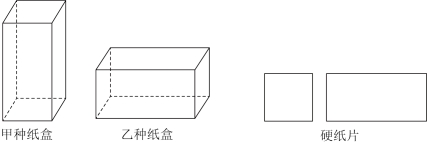
(1)现用200张正方形硬纸片和400张长方形硬纸片,恰好能制作甲、乙两种纸盒各多少个?
(2)如果需要制作100个长方体纸盒,要求乙种纸盒数量不低于甲种纸盒数量的一半,那么至少需要多少张正方形硬纸片?
23. 如图,港口![]() 位于岛
位于岛![]() 的北偏西
的北偏西![]() 方向,灯塔
方向,灯塔![]() 在岛
在岛![]() 的正东方向,
的正东方向,![]() ,一艘海轮
,一艘海轮![]() 在岛
在岛![]() 的正北方向,且
的正北方向,且![]() 、
、![]() 、
、![]() 三点在一条直线上,
三点在一条直线上,![]() .
.
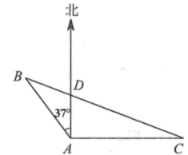
(1)求岛![]() 与港口
与港口![]() 之间的距离;
之间的距离;
(2)求![]() .
.
(参考数据:![]() ,
,![]() ,
,![]() )
)
24. 已知二次函数![]() ,
,![]() 为常数.
为常数.
(1)若该二次函数的图像与直线![]() 有两个交点,求
有两个交点,求![]() 的取值范围;
的取值范围;
(2)若该二次函数的图像与![]() 轴有交点,求
轴有交点,求![]() 的值;
的值;
(3)求证:该二次函数的图像不经过原点.
25. 一块直角三角形木板,它的一条直角边![]() 长
长![]() ,面积为
,面积为![]() .
.
(1)甲、乙两人分别按图1、图2用它设计一个正方形桌面,请说明哪个正方形面积较大;
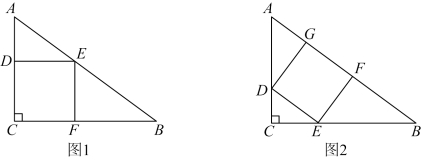
(2)丙、丁两人分别按图3、图4用它设计一个长方形桌面.请分别求出图3、图4中长方形的面积![]() 与
与![]() 的长
的长![]() 之间的函数表达式,并分别求出面积的最大值.
之间的函数表达式,并分别求出面积的最大值.
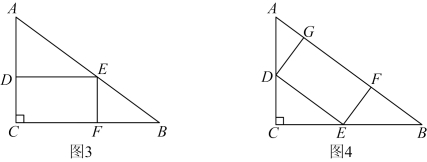
26. 已知![]() 是
是![]() 的高,
的高,![]() 是
是![]() 的外接圆.
的外接圆.
(1)请你在图1中用无刻度的直尺和圆规,作![]() 的外接圆(保留作图痕迹,不写作法);
的外接圆(保留作图痕迹,不写作法);
(2)如图2,若![]()
![]() 半径为
半径为![]() ,求证:
,求证:![]() ;
;
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,过点
,过点![]()
![]() 切线交
切线交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
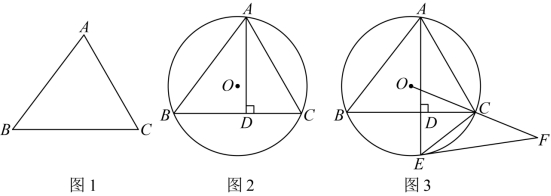
27. 综合与实践
【问题情境】
如图,小昕同学在正方形纸板![]() 的边
的边![]() 、
、![]() 上分别取点
上分别取点![]() 、
、![]() ,且
,且![]() ,
,![]() 交
交![]() 于点
于点![]() .连接
.连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
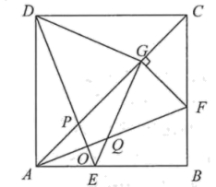
【活动猜想】
(1)![]() 与
与![]() 的数量关系是_______,位置关系是_______;
的数量关系是_______,位置关系是_______;
【探索发现】
(2)证明(1)中的结论;
【实践应用】
(3)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
【综合探究】(4)若![]() ,则当
,则当![]() _______时,
_______时,![]()
![]() 面积最小
面积最小
参考答案
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项符合题目要求,请将正确选项前的字母代号填涂在答题卡相应位置上)
【1题答案】
【答案】A
【2题答案】
【答案】C
【3题答案】
【答案】D
【4题答案】
【答案】B
【5题答案】
【答案】C
【6题答案】
【答案】A
【7题答案】
【答案】C
【8题答案】
【答案】A
二、填空题(本大题共8小题,每小题3分,共24分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)
【9题答案】
【答案】2a
【10题答案】
【答案】![]()
【11题答案】
【答案】![]()
【12题答案】
【答案】![]()
【13题答案】
【答案】![]()
【14题答案】
【答案】16000
【15题答案】
【答案】![]()
【16题答案】
【答案】![]()
三、解答题(本大题共11小题,共102分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤,作图过程需保留作图痕迹)
【17题答案】
【答案】6
【18题答案】
【答案】![]()
【19题答案】
【答案】![]()
【20题答案】
【答案】(1)![]()
(2)![]()
【21题答案】
【答案】(1)![]() ,
,![]()
(2)![]()
(3)![]() 人
人
【22题答案】
【答案】(1)恰好能制作甲种纸盒40个,乙种纸盒80个
(2)至少需要134张正方形硬纸片
【23题答案】
【答案】(1)![]()
(2)![]()
【24题答案】
【答案】(1)![]()
(2)![]()
(3)
【25题答案】
【答案】(1)图1的正方形面积较大
(2)在图3中,![]() ,当
,当![]() 时,长方形的面积有最大值为
时,长方形的面积有最大值为![]() ;在图4中,
;在图4中,![]() ,当
,当![]() 时,长方形的面积有最大值为
时,长方形的面积有最大值为![]()
【26题答案】
【答案】
(1)
 (2)
(2)
(3)![]()
【27题答案】
【答案】(1)相等,垂直
(2)
(3)![]()
(4)![]()
