2024年新疆中考数学试题及答案
一、单项选择题(本大题共9小题,每小题4分,共36分)
1. 下列实数中,比0小的数是( )
A. ![]() B. 0.2C.
B. 0.2C. ![]() D. 1
D. 1
【答案】A
【解析】
【分析】本题考查了正数、负数的大小比较,正数大于一切负数和0,0大于一切负数.正数大于负数和0,0大于负数,也就是负数小于0,据此即可求解.
【详解】解:因为小于0的数是负数,
所以![]() 比0小,
比0小,
故选:A.
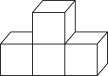
2. 四个大小相同的正方体搭成的几何体如图所示,它的主视图是( )
A. 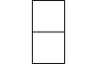 B.
B. 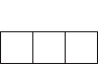 C.
C. 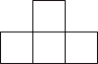 D.
D. 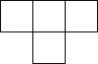
【答案】C
【解析】
【分析】本题主要考查了三视图,画出从前面看到图形,即可.
【详解】解:它的主视图是:
,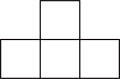
故选:C.
3. 下列运算正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
【分析】本题考查了整式的运算,根据合并同类项法则、同底数幂的乘法和除法、积的乘方运算法则分别计算即可判断求解,掌握整式的运算法则是解题的关键.
【详解】解:![]() 、
、![]() ,该选项错误,不合题意;
,该选项错误,不合题意;
![]() 、
、![]() ,该选项正确,符合题意;
,该选项正确,符合题意;
![]() 、
、![]() ,该选项错误,不合题意;
,该选项错误,不合题意;
![]() 、
、![]() ,该选项错误,不合题意;
,该选项错误,不合题意;
故选:![]() .
.
4. 估计![]() 的值在( )
的值在( )
A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间
【答案】A
【解析】
【分析】本题主要考查无理数的估算,掌握无理数的估算方法是解题的关键.根据无理数的估算方法计算即可.
【详解】解:∵![]() ,
,
∴![]() ,即
,即![]() ,
,
故选:A.
5. 某跳远队准备从甲、乙、丙、丁4名运动员中选取1名成绩优异且发挥稳定的运动员参加比赛,他们成绩的平均数和方差如下:![]() ,则应选择的运动员是( )
,则应选择的运动员是( )
A. 甲B. 乙C. 丙D. 丁
【答案】C
【解析】
【分析】本题主要考查利用平均数、方差作决策,解题的关键是熟知平均数、方差的意义.根据平均数与方差的意义即可判断.
【详解】解:∵![]()
∴选择乙、丙,
∵![]() ,
,
∴选择丙,
故选:C.
6. 如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,
的弦,![]() ,垂足为E.若
,垂足为E.若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )

A. 1B. 2C. 3D. 4
【答案】B
【解析】
【分析】本题考查了垂径定理,勾股定理的应用,熟练掌握知识点是解题的关键.
根据垂径定理求得![]() ,再对
,再对![]() 运用勾股定理即可求
运用勾股定理即可求![]() ,最后
,最后![]() 即可求解.
即可求解.
【详解】解:∵![]() ,
,![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,![]() ,
,
∴在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
∴![]() ,
,
故选:B.
7. 若一次函数![]() 的函数值y随x的增大而增大,则k的值可以是( )
的函数值y随x的增大而增大,则k的值可以是( )
A. ![]() B.
B. ![]() C. 0D. 1
C. 0D. 1
【答案】D
【解析】
【分析】本题考查了一次函数的性质,要知道,在直线![]() 中,当
中,当![]() 时,y随x的增大而增大;当
时,y随x的增大而增大;当![]() 时,y随x的增大而减小.
时,y随x的增大而减小.
【详解】解:∵一次函数![]() 的函数值y随x的增大而增大,
的函数值y随x的增大而增大,
∴![]() ,
,
而四个选项中,只有D符合题意,
故选:D.
8. 某校九年级学生去距学校![]() 的科技馆研学,一部分学生乘甲车先出发,
的科技馆研学,一部分学生乘甲车先出发,![]() 后其余学生再乘乙车出发,结果同时到达.已知乙车的速度是甲车速度的1.2倍,设甲车的速度为
后其余学生再乘乙车出发,结果同时到达.已知乙车的速度是甲车速度的1.2倍,设甲车的速度为![]() ,根据题意可列方程( )
,根据题意可列方程( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
【分析】本题考查了分式方程的应用,正确理解题意是解决本题的关键.
先把时间化为小时,设甲车的速度为![]() ,则乙车的速度为
,则乙车的速度为![]() ,表示出两车的时间,再根据时间相差5分钟建立方程即可.
,表示出两车的时间,再根据时间相差5分钟建立方程即可.
【详解】解:![]() ,设甲车的速度为
,设甲车的速度为![]() ,根据题意可列方程:
,根据题意可列方程:
![]() ,
,
故选:D.
9. 如图,在平面直角坐标系中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,
两点,![]() 轴于点
轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,结合图象判断下列结论:
,结合图象判断下列结论:![]() 点
点![]() 与点
与点![]() 关于原点对称;
关于原点对称;![]() 点
点![]() 是
是![]() 的中点;
的中点;![]() 在
在![]() 的图象上任取点
的图象上任取点![]() 和点
和点![]() ,如果
,如果![]() ,那么
,那么![]() ;
;![]()
![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
【分析】本题考查了一次函数与反比例函数的交点问题,反比例函数的性质,根据反比例函数的性质逐项判断即可求解,掌握反比例函数的性质是解题的关键.
【详解】解:∵直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,
两点,
∴点![]() 与点
与点![]() 关于原点对称,故
关于原点对称,故![]() 正确;
正确;
∵点![]() 与点
与点![]() 关于原点对称,
关于原点对称,
∴![]() ,
,
∵![]() 轴,
轴,![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 是
是![]() 的中点,故
的中点,故![]() 正确;
正确;
∵![]() ,
,
∴在每一象限内,![]() 随
随![]() 的增大而减小,
的增大而减小,
当![]() 在同一象限内时,如果
在同一象限内时,如果![]() ,那么
,那么![]() ;当
;当![]() 不在同一象限内时,如果
不在同一象限内时,如果![]() ,那么
,那么![]() ,故
,故![]() 错误;
错误;
∵![]() 轴,
轴,
∴![]() ,
,
∵点![]() 与点
与点![]() 关于原点对称,
关于原点对称,
∴![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() ,故
,故![]() 正确;
正确;
∴正确结论有![]() 个,
个,
故选:![]() .
.
二、填空题(本大题共6小题,每小题4分,共24分)
10. 若每个篮球30元,则购买n个篮球需_____________元.
【答案】![]()
【解析】
【分析】本题考查了列代数式,熟练掌握代数式的书写格式是解题的关键. 根据总价=数量×单价,进而求出篮球的总价即可.
【详解】解:若每个篮球30元,则购买n个篮球需![]() 元,
元,
故答案为:![]() .
.
11. 学校广播站要新招1名广播员,甲、乙两名同学经过选拔进入到复试环节,参加了口语表达、写作能力两项测试,成绩如下表:
项目 应试者 | 口语表达 | 写作能力 |
甲 | 80 | 90 |
乙 | 90 | 80 |
学校规定口语表达按![]() ,写作能力按
,写作能力按![]() 计入总成绩,根据总成绩择优录取.通过计算,你认
计入总成绩,根据总成绩择优录取.通过计算,你认![]() _____________同学将被录取.
_____________同学将被录取.
【答案】乙
【解析】
【分析】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.根据加权平均数的定义列式计算即可得出答案.
【详解】解:甲的总成绩为![]() ,
,
乙的总成绩为![]() ,
,
∵![]() ,
,
∴乙同学被录取,
故答案为:乙.
12. 若关于x的一元二次方程![]() 有两个不相等的实数根,则k的取值范围为_____________.
有两个不相等的实数根,则k的取值范围为_____________.
【答案】![]()
【解析】
【分析】本题主要考查了一元二次方程根的判别式,熟练掌握一元二次方程![]() ,当
,当![]() 时,方程有两个不相等的实数根;当
时,方程有两个不相等的实数根;当![]() 时,方程有两个相等的实数根;当
时,方程有两个相等的实数根;当![]() 时,方程没有实数根是解题的关键.利用一元二次方程根的判别式,即可求解.
时,方程没有实数根是解题的关键.利用一元二次方程根的判别式,即可求解.
【详解】解:∵一元二次方程![]() 有两个不相等的实数根,
有两个不相等的实数根,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() .
.
13. 如图,在正方形![]() 中,若面积
中,若面积![]() ,周长
,周长![]() ,则
,则![]() _________.
_________.
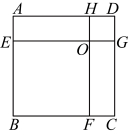
【答案】40
【解析】
【分析】本题考查了正方形、矩形的性质,完全平方公式等知识,设正方形![]() 、
、![]() 的边长分别为a、b,先求出
的边长分别为a、b,先求出![]() ,然后根据
,然后根据![]() 求解即可.
求解即可.
【详解】解:设正方形![]() 、
、![]() 的边长分别为a、b,
的边长分别为a、b,
根据题意,得 ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]() ,
,
故答案为:40.
14. 如图,在![]() 中,
中,![]() .若点D在直线
.若点D在直线![]() 上(不与点A,B重合),且
上(不与点A,B重合),且![]() ,则
,则![]() 的长为_____________.
的长为_____________.
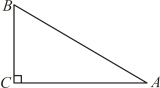
【答案】6或12
【解析】
【分析】本题考查了含![]() 的直角三角形的性质,三角形外角的性质,等角对等边等知识,分①点D在线段
的直角三角形的性质,三角形外角的性质,等角对等边等知识,分①点D在线段![]() 时,②点D在线段
时,②点D在线段![]() 延长线上时, ③点D在线段
延长线上时, ③点D在线段![]() 延长线上时,三种情况讨论求解即可.
延长线上时,三种情况讨论求解即可.
【详解】解:∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
①点D在线段![]() 时,
时,

∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②点D在线段![]() 延长线上时,
延长线上时,

∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
③点D![]() 线段
线段![]() 延长线上时,
延长线上时,
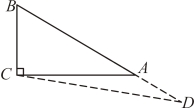
此时![]() ,即
,即![]() ,故不符合题意,舍去,
,故不符合题意,舍去,
综上,![]() 的长为6或12.
的长为6或12.
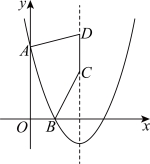
15. 如图,抛物线![]() 与y轴交于点A,与x轴交于点B,线段
与y轴交于点A,与x轴交于点B,线段![]() 在抛物线的对称轴上移动(点C在点D下方),且
在抛物线的对称轴上移动(点C在点D下方),且![]() .当
.当![]() 的值最小时,点C的坐标为_____________.
的值最小时,点C的坐标为_____________.
【答案】![]()
【解析】
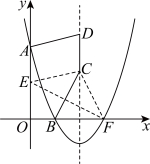
【分析】在y轴上取点![]() ,证明四边形
,证明四边形![]() 是平行四边形,得出
是平行四边形,得出![]() ,利用抛物线的对称性得出
,利用抛物线的对称性得出![]() ,则
,则![]() ,当E、C、F三点共线时,
,当E、C、F三点共线时,![]() 最小,利用待定系数法求出直线
最小,利用待定系数法求出直线![]() 解析式,然后把
解析式,然后把![]() 代入,即可求出C的坐标.
代入,即可求出C的坐标.
【详解】解:![]() ,
,
∴对称轴为![]() ,
,
如图,设抛物线与x轴另一个交点为F,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在y轴上取点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵抛物线对称轴![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
当E、C、F三点共线时,![]() 最小,
最小,
设直线![]() 解析式为
解析式为![]() ,
,
∴![]() ,
,
解得 ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴当![]() 最小时,C的坐标为
最小时,C的坐标为![]() ,
,
故答案为:![]() .
.
【点睛】本题考查了二次函数的性质,平行四边形的判定与性质,待定系数法求一次函数解析式,两点之间线段最短等知识,明确题意,添加合适辅助线,构造平行四边形是解题的关键.
三、解答题(本大题共8小题,共90分.解答应写出必要的文字说明、证明过程或演算步骤)
16. 计算:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)7 (2)1
【解析】
【分析】本题考查了实数的运算,分式的运算,解题的关键是:
(1)利用绝对值的意义,乘方法则,算术平方根的定义,零指数幂的意义化简计算即可;
(2)先把第一个分式的分子、分母因式分解,同时把除法转化为乘法,然后约分化简即可.
【小问1详解】
解:原式![]()
![]() ;
;
【小问2详解】
解:原式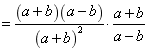
![]() .
.
17. (![]() )解方程:
)解方程:![]() ;
;
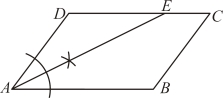
(![]() )如图,已知平行四边形
)如图,已知平行四边形![]() .
.
![]() 尺规作图:请用无刻度的直尺和圆规,作
尺规作图:请用无刻度的直尺和圆规,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ;(要求:不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
;(要求:不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
![]() 在
在![]() 的条件下,求证:
的条件下,求证:![]() 是等腰三角形.
是等腰三角形.

【答案】(![]() )
)![]() ;(
;(![]() )
)![]() 作图见解析;
作图见解析;![]() 证明见解析.
证明见解析.
【解析】
【分析】(![]() )按照解一元一次方程的步骤解答即可求解;
)按照解一元一次方程的步骤解答即可求解;
(![]() )
)![]() 按照作角平分线的方法作图即可;
按照作角平分线的方法作图即可;![]() 由平行四边形的性质及角平分线的性质可得
由平行四边形的性质及角平分线的性质可得![]() ,即得
,即得![]() ,即可求证;
,即可求证;
本题考查了解一元一次方程,作角![]() 平分线,角平分线的性质,平行四边形的性质,等腰三角形的判定,根据题意正确画出图形是解题的关键.
平分线,角平分线的性质,平行四边形的性质,等腰三角形的判定,根据题意正确画出图形是解题的关键.
【详解】(![]() )解:去括号得,
)解:去括号得,![]() ,
,
移项得,![]() ,
,
合并同类项得,![]() ;
;
(![]() )
)![]() 解:如图,
解:如图,![]() 即为所求;
即为所求;
![]() ∵四边形
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形.
是等腰三角形.
18. 为丰富学生的校园生活,提升学生的综合素质,某校计划开设丰富多彩的社团活动.为了解全校学生对各类社团活动的喜爱情况,该校随机抽取部分学生进行问卷调查(每名学生必选且只选一类),并根据调查结果制成如下统计图(不完整):

结合调查信息,回答下列问题:
(1)本次共调查了 名学生,喜爱“艺术类”社团活动的学生人数是 ;
(2)若该校有1000名学生,请估计其中大约有多少名学生喜爱“阅读类”社团活动?
(3)某班有2名男生和1名女生参加“体育类”社团中“追风篮球社”的选拔,2名学生被选中.请用列表法或画树状图法求选中的2名学生恰好为1名男生和1名女生的概率.
【答案】(1)100,25
(2)150 (3)![]()
【解析】
【分析】本题考查了条形统计图与扇形统计图,用样本估计总体,用列表法或树状图法求概率,解题的关键是:
(1)用“体育类”人数除以所占百分比求出被调查人数,用总人数乘以“艺术类”所占百分比即可;
(2)用1000乘以“阅读类”所占百分比即可;
(3)画树状图展示所有6种等可能的结果,再找出一名男生和一名女生的结果数,然后根据概率公式求解.
【小问1详解】
解:本次共调查学生人数为![]() ,
,
喜爱“艺术类”社团活动的学生人数是![]() ,
,
故答案为:100,25;
【小问2详解】
解:![]() ,
,
答:大约有150名学生喜爱“阅读类”社团活动;
【小问3详解】
解:画树状图,如下
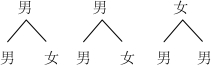
共有6种等可能的结果,其中抽取的两人恰好是一名男生和一名女生的结果数为4,
∴抽取的两人恰好是一名男生和一名女生概率为![]() .
.
19. 如图,![]() 的中线
的中线![]() ,
,![]() 交于点O,点F,G分别是
交于点O,点F,G分别是![]() ,
,![]() 的中点.
的中点.
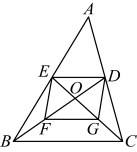
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 时,求证:
时,求证:![]() 是矩形.
是矩形.
【答案】(1)见解析 (2)见解析
【解析】
【分析】本题考查了平行四边形的判定与性质,矩形的判断,三角形中位线定理等知识,解题的关键是:
(1)利用三角形中位线定理可得出![]() ,
,![]() ,然后利用平行四边形的判定即可得证;
,然后利用平行四边形的判定即可得证;
(2)利用平行四边形的性质得出![]() ,
,![]() ,结合点G是
,结合点G是![]() 的中点,可得出
的中点,可得出![]() ,同理
,同理![]() ,则可得出
,则可得出![]() ,
,![]() ,然后利用矩形判定即可得证.
,然后利用矩形判定即可得证.
【小问1详解】
证明:∵![]() 的中线
的中线![]() ,
,![]() 交于点O,
交于点O,
∴![]() ,
,![]() ,
,
∵点F,G分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
【小问2详解】
证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∵G是![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
同理![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() 是矩形.
是矩形.
20. 数学活动课上为了测量学校旗杆的高度,某小组进行了以下实践活动:
(1)准备测量工具
①测角仪:把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小重物,制成一个简单的测角仪(图1),利用它可以测量仰角或俯角;
②皮尺.

(2)实地测量数据
①将这个测角仪用手托起,拿到眼前,使视线沿着测角仪的直径刚好到达旗杆的最高点(图2);
②用皮尺测出所站位置到旗杆底部的距离为![]() ,眼睛到地面的距离为
,眼睛到地面的距离为![]() .
.
(3)计算旗杆高度
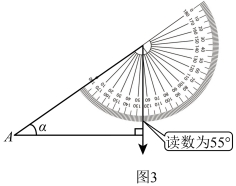
①根据图3中测角仪的读数,得出仰角![]() 的度数为 ;
的度数为 ;
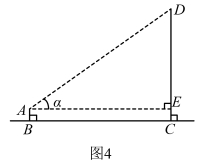
②根据测量数据,画出示意图4,![]() ,求旗杆
,求旗杆![]() 的高度(精确到
的高度(精确到![]() );(参考数据:
);(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
③若测量者仍站在原处(B点),能否用三角板替代测角仪测出仰角![]() ?若能,请写出测量方法;若不能,该如何调整位置才能用三角板测出仰角
?若能,请写出测量方法;若不能,该如何调整位置才能用三角板测出仰角![]() ,请写出测量方法.
,请写出测量方法.

【答案】①![]() ;②
;②![]() ;③不能,见详解
;③不能,见详解
③不能,
若使用![]() 的三角板,可以把三角板的
的三角板,可以把三角板的![]() 角对着眼睛,直角边在水平线上,视线沿着三角板的斜边向上看,然后向后退,直至退到
角对着眼睛,直角边在水平线上,视线沿着三角板的斜边向上看,然后向后退,直至退到![]() 角的顶点与点D重合即可停下,即得到此时的仰角为
角的顶点与点D重合即可停下,即得到此时的仰角为![]() ,标记自己的位置,测量自己的位置与点C的距离,即可解直角三角形进行计算,如示意图:
,标记自己的位置,测量自己的位置与点C的距离,即可解直角三角形进行计算,如示意图:
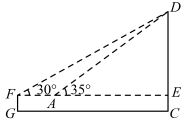
若使用![]() 的三角板,可以把三角板的
的三角板,可以把三角板的![]() 角对着眼睛,直角边在水平线上,视线沿着三角板的斜边向上看,然后向前走,直至走到另一个
角对着眼睛,直角边在水平线上,视线沿着三角板的斜边向上看,然后向前走,直至走到另一个![]() 角的顶点与点D重合即可停下,即得到此时的仰角为
角的顶点与点D重合即可停下,即得到此时的仰角为![]() ,标记自己的位置,测量自己的位置与点C的距离,即可解直角三角形进行计算,如示意图:
,标记自己的位置,测量自己的位置与点C的距离,即可解直角三角形进行计算,如示意图:

21. 某公司销售一批产品,经市场调研发现,当销售量在0.4吨至3.5吨之间时,销售额![]() (万元)与销售量x(吨)的函数解析式为
(万元)与销售量x(吨)的函数解析式为![]() ;成本
;成本![]() (万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中
(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中![]() 是其顶点.
是其顶点.
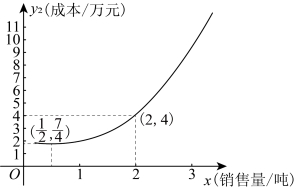
(1)求出成本![]() 关于销售量x的函数解析式;
关于销售量x的函数解析式;
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?(注:利润=销售额![]() 成本)
成本)
【答案】(1)![]()
(2)销售产品所获利润是<img height="19" src="//img.985ks.com/images_new/img_default_show.png" data-src="//img.985ks.com/uploadfile/images/2025/0610/17495656488609648.pn
万元;
(3)当销售量![]() 吨时,获得最大利润,最大利润为:
吨时,获得最大利润,最大利润为:![]() 万元;
万元;
22. 如图,在![]() 中,
中,![]() 是
是![]() 的直径,弦
的直径,弦![]() 交
交![]() 于点E,
于点E,![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析 (2)![]()
【解析】
【小问1详解】
证明:∵![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ;
;
23. 【探究】
(![]() )已知
)已知![]() 和
和![]() 都是等边三角形.
都是等边三角形.
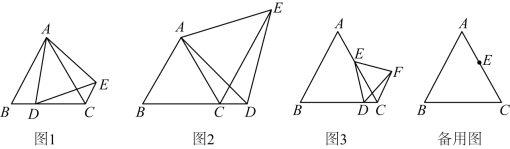
①如图![]() ,当点
,当点![]() 在
在![]() 上时,连接
上时,连接![]() .请探究
.请探究![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
②如图![]() ,当点
,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() .请再次探究
.请再次探究![]() 和
和![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【运用】
(![]() )如图
)如图![]() ,等边三角形
,等边三角形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() .点
.点![]() 是直线
是直线![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作等边三角形
的右侧作等边三角形![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,请直接写出
为直角三角形时,请直接写出![]() 的长.
的长.
【答案】(![]() )
)![]()
![]() ;
;![]()
![]() ;(
;(![]() )
)![]() 或
或![]() .
.
