2023年新疆中考数学试题及答案
一、单项选择题(本大题共9小题,每小题4分,共36分.请按答题卷中的要求作答)
1. ﹣5的绝对值是( )
A. 5 B. ﹣5 C. ![]() D.
D. ![]()
2. 下列交通标志中是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
3. 我国自主研制的全球最大集装箱船“地中海泰莎”号的甲板面积近似于4个标准足球场,可承载![]() 吨的货物,数字
吨的货物,数字![]() 用科学记数法可表示为( )
用科学记数法可表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 一次函数![]() 的图象不经过( )
的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 计算![]() 的结果是( )
的结果是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 用配方法解一元二次方程![]() ,配方后得到的方程是( )
,配方后得到的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 如图,在![]() 中,若
中,若![]() ,
,![]() ,则扇形
,则扇形![]() (阴影部分)的面积是( )
(阴影部分)的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
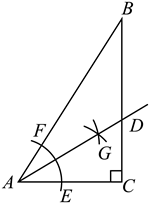
8. 如图,在![]() 中,以点
中,以点![]() 为圆心,适当长为半径作弧,交
为圆心,适当长为半径作弧,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 长为半径作弧,两弧在
长为半径作弧,两弧在![]() 的内部交于点
的内部交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
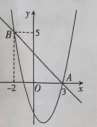
9. 如图,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() ,
,![]() .结合图象,判断下列结论:①当
.结合图象,判断下列结论:①当![]() 时,
时,![]() ;②
;②![]() 是方程
是方程![]() 的一个解;③若
的一个解;③若![]() ,
,![]() 是抛物线上的两点,则
是抛物线上的两点,则![]() ;④对于抛物线,
;④对于抛物线,![]() ,当
,当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题(本大题共6小题,每小题4分,共24分.请按答题卷中的要求作答)
10. 要使分式![]() 有意义,则x需满足的条件是______.
有意义,则x需满足的条件是______.
11. 若正多边形的一个内角等于![]() ,则这个正多边形的边数是 ______.
,则这个正多边形的边数是 ______.
12. 在平面直角坐标系中有五个点,分别是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从中任选一个点恰好在第一象限的概率是______.
,从中任选一个点恰好在第一象限的概率是______.
13. 如图,在![]() 中,若
中,若![]() ,
,![]() ,
,![]() ,则
,则![]() ______
______![]() .
.

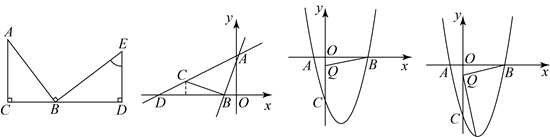
14. 如图,在平面直角坐标系中,![]() 为直角三角形,
为直角三角形,![]() ,
,![]() ,
,![]() .若反比例函数
.若反比例函数![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ______.
______.

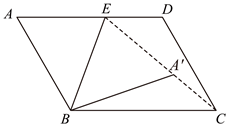
15. 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一动点,将
上一动点,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,当点
,当点![]() 恰好落在
恰好落在![]() 上时,
上时,![]() 的长为______.
的长为______.
三、解答题(本大题共8小题,共90分.解答应写出必要的文字说明、证明过程或演算步骤)
16 计算:
(1)![]() ;
;
(2)![]() .
.
17. (1)解不等式组:
(2)金秋时节,新疆瓜果飘香.某水果店A种水果每千克5元,B种水果每千克8元,小明买了A、B两种水果共7千克花了41元.A、B两种水果各买了多少千克?
18. 如图,![]() 和
和![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .点
.点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
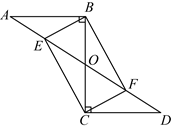
(1)求证:![]() ;
;
(2)当![]() 时,求证:四边形
时,求证:四边形![]() 是矩形.
是矩形.
19. 跳绳是某校体育活动的特色项目.体育组为了了解七年级学生1分钟跳绳次数情况,随机抽取20名七年级学生进行1分钟跳绳测试(单位:次),数据如下:
100 110 114 114 120 122 122 131 144 148
152 155 156 165 165 165 165 174 188 190
对这组数据进行整理和分析,结果如下:
平均数 | 众数 | 中位数 |
145 |
|
|
请根据以上信息解答下列问题:
(1)填空:![]() ______,
______,![]() ______;
______;
(2)学校规定1分钟跳绳165次及以上为优秀,请你估计七年级240名学生中,约有多少名学生能达到优秀?
(3)某同学1分钟跳绳152次,请推测该同学的1分钟跳绳次数是否超过年级一半的学生?说明理由.
20. 烽燧即烽火台,是古代军情报警的一种措施,史册记载,夜间举火称“烽”,白天放烟称“燧”.克孜尔尕哈烽燧是古丝绸之路北道上新疆境内时代最早、保存最完好、规模最大的古代烽燧(如图1).某数学兴趣小组利用无人机测量该烽燧的高度,如图2,无人机飞至距地面高度![]() 米的A处,测得烽燧
米的A处,测得烽燧![]() 的顶部C处的俯角为
的顶部C处的俯角为![]() ,测得烽燧
,测得烽燧![]() 的底部B处的俯角为
的底部B处的俯角为![]() ,试根据提供的数据计算烽燧
,试根据提供的数据计算烽燧![]() 的高度.(参数据:
的高度.(参数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

21. 随着端午节的临近,![]() ,
,![]() 两家超市开展促销活动,各自推出不同的购物优惠方案,如下表:
两家超市开展促销活动,各自推出不同的购物优惠方案,如下表:
|
| |
优惠方案 | 所有商品按八折出售 | 购物金额每满 |
(1)当购物金额为![]() 元时,选择超市______(填“
元时,选择超市______(填“![]() ”或“
”或“![]() ”)更省钱;
”)更省钱;
当购物金额为![]() 元时,选择超市______(填“
元时,选择超市______(填“![]() ”或“
”或“![]() ”)更省钱;
”)更省钱;
(2)若购物金额为![]() (
(![]() )元时,请分别写出它们的实付金额
)元时,请分别写出它们的实付金额![]() (元)与购物金额
(元)与购物金额![]() (元)之间的函数解析式,并说明促销期间如何选择这两家超市去购物更省钱?
(元)之间的函数解析式,并说明促销期间如何选择这两家超市去购物更省钱?
(3)对于![]() 超市的优惠方案,随着购物金额的增大,顾客享受的优惠率不变,均为
超市的优惠方案,随着购物金额的增大,顾客享受的优惠率不变,均为![]() %(注:
%(注:![]() ).若在
).若在![]() 超市购物,购物金额越大,享受的优惠率一定越大吗?请举例说明.
超市购物,购物金额越大,享受的优惠率一定越大吗?请举例说明.
22. 如图,![]() 是
是![]() 的直径,点
的直径,点![]() ,
,![]() 是
是![]() 上的点,且
上的点,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
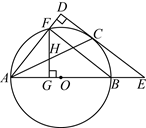
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
23. 【建立模型】(1)如图![]() ,点
,点![]() 是线段
是线段![]() 上的一点,
上的一点,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,
,![]() .求证:
.求证:![]() ;
;
【类比迁移】(2)如图![]() ,一次函数
,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、与
、与![]() 轴交于点
轴交于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() 、直线
、直线![]() 交
交![]() 轴于点
轴于点![]() .
.
①求点![]() 的坐标;
的坐标;
②求直线![]() 的解析式;
的解析式;
【拓展延伸】(3)如图![]() ,抛物线
,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点
两点![]() 点
点![]() 在点
在点![]() 的左侧
的左侧![]() ,与
,与![]() 轴交于
轴交于![]() 点,已知点
点,已知点![]() ,
,![]() ,连接
,连接![]() .抛物线上是否存在点
.抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的横坐标.
的横坐标.
参考答案
一、单项选择题(本大题共9小题,每小题4分,共36分.请按答题卷中的要求作答)
【1题答案】
【答案】A
【2题答案】
【答案】B
【3题答案】
【答案】A
【4题答案】
【答案】D
【5题答案】
【答案】C
【6题答案】
【答案】D
【7题答案】
【答案】B
【8题答案】
【答案】C
【9题答案】
【答案】B
二、填空题(本大题共6小题,每小题4分,共24分.请按答题卷中的要求作答)
【10题答案】
【答案】![]()
【11题答案】
【答案】10##十
【12题答案】
【答案】![]()
【13题答案】
【答案】![]()
【14题答案】
【答案】![]()
【15题答案】
【答案】![]() ##
##![]()
三、解答题(本大题共8小题,共90分.解答应写出必要的文字说明、证明过程或演算步骤)
【16题答案】
【答案】(1)![]()
(2)![]()
【17题答案】
【答案】(1)![]() ;(2)购买A种水果5千克,则购买B种水果
;(2)购买A种水果5千克,则购买B种水果![]() 千克
千克
【18题答案】
【答案】(1)见解析 (2)见解析
【19题答案】
【答案】(1)![]() ,
,![]()
(2)![]()
(3)是,理由见解析
【20题答案】
【答案】![]() 米
米
【21题答案】
【答案】(1)![]() ,
,![]()
(2)![]() ,
, ,当
,当![]() 或
或![]() 时选择
时选择![]() 超市更省钱,当
超市更省钱,当![]() 时,选择
时,选择![]() 超市更省钱
超市更省钱
(3)不一定,理由见解析
【22题答案】
【答案】(1)见解析 (2)![]()
【23题答案】
【答案】[建立模型](1)见解析; [类比迁移] (2)①![]() ;②直线
;②直线![]() 的解析式为
的解析式为![]() ,[拓展延伸](3)
,[拓展延伸](3)![]() 或
或![]()
