2025年天津高考数学试题及答案
第I卷(选择题)
参考公式:
·如果事件![]() 互斥,那么
互斥,那么![]()
·如果事件![]() 相互独立,那么
相互独立,那么![]()
·棱柱的体积公式![]() ,其中S表示棱柱的底面面积,h表示棱柱的高.
,其中S表示棱柱的底面面积,h表示棱柱的高.
·圆锥的体积公式![]() ,其中S表示圆锥的底面面积,h表示圆锥的高.
,其中S表示圆锥的底面面积,h表示圆锥的高.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的
1. 已知集合![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 设![]() ,则“
,则“![]() ”是“
”是“![]() ”的( )
”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
3. 已知函数![]() 的图象如下,则
的图象如下,则![]() 的解析式可能为( )
的解析式可能为( )
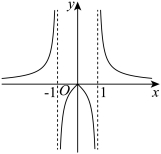
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 若m为直线,![]() 为两个平面,则下列结论中正确的是( )
为两个平面,则下列结论中正确的是( )
A. 若![]() ,则
,则![]() B. 若
B. 若![]() ,则
,则![]()
C. 若![]() ,则
,则![]() D. 若
D. 若![]() ,则
,则![]()
5. 下列说法中错误的是( )
A. 若![]() ,则
,则![]()
B. 若![]() ,
,![]() ,则
,则![]()
C. ![]() 越接近1,相关性越强
越接近1,相关性越强
D. ![]() 越接近0,相关性越弱
越接近0,相关性越弱
6. ![]() ,则数列
,则数列![]() 的前
的前![]() 项和为( )
项和为( )
A![]() 112B. 48C. 80D. 64
112B. 48C. 80D. 64
7. 函数![]() 的零点所在区间是( )
的零点所在区间是( )
A![]()
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. ![]() ,在
,在![]() 上单调递增,且
上单调递增,且![]() 为它的一条对称轴,
为它的一条对称轴,![]() 是它的一个对称中心,当
是它的一个对称中心,当![]() 时,
时,![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C. 1D. 0
C. 1D. 0
9. 双曲线![]()
![]() 左、右焦点分别为
左、右焦点分别为![]() ,以右焦点
,以右焦点![]() 为焦点的抛物线
为焦点的抛物线![]() 与双曲线交于另一象限点为P,若
与双曲线交于另一象限点为P,若![]() ,则双曲线的离心率
,则双曲线的离心率![]() ( )
( )
A. 2B. 5C. ![]() D.
D. ![]()
第Ⅱ卷(非选择题)
注意事项:
1.用黑色墨水的钢笔或签字笔将答案写在答题卡上.
2.本卷共11小题,共105分.
二、填空题:本大题共6个小题,每小题5分,共30分.
10. 已知i是虚数单位,则![]() ________.
________.
11. 在![]() 的展开式中,
的展开式中,![]() 项的系数为________.
项的系数为________.
12. ![]() ,与x轴交于点A,与y轴交于点B,与
,与x轴交于点A,与y轴交于点B,与![]() 交于C、D两点,
交于C、D两点,![]() ,则
,则![]() _________.
_________.
13. 小桐操场跑圈,一周2次,一次5圈或6圈.第一次跑5圈或6圈的概率均为0.5,若第一次跑5圈,则第二次跑5圈的概率为0.4,6圈的概率为0.6;若第一次跑6圈,则第二次跑5圈的概率为0.6,4圈的概率为0.4.小桐一周跑11圈的概率为________;若一周至少跑11圈为动量达标,则连续跑4周,记合格周数为X,则期望![]() _______
_______
14. ![]() 中,D为AB边中点,
中,D为AB边中点,![]() ,则
,则![]() ______(用
______(用![]() ,
,![]() 表示),若
表示),若![]() ,
,![]() ,则
,则![]() _______
_______
15. 若![]() ,对
,对![]() ,均有
,均有![]() 恒成立,则
恒成立,则![]() 的最小值为_______
的最小值为_______
三、解答题:本大题共5小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16. 在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() .已知
.已知![]() ,
,![]() ,
,![]() .
.
(1)求A的值;
(2)求c的值;
(3)求![]() 的值.
的值.
17. 正方体![]()
![]() 棱长为4,
棱长为4,![]() 分别为
分别为![]() 中点,
中点,![]()
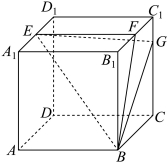
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 夹角的余弦值;
夹角的余弦值;
(3)求三棱锥![]() 的体积.
的体积.
18. 已知椭圆![]() 的左焦点为F,右顶点为A,P为
的左焦点为F,右顶点为A,P为![]() 上一点,且直线
上一点,且直线![]() 的斜率为
的斜率为![]() ,
,![]() 的面积为
的面积为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的方程;
(2)过点P的直线与椭圆有唯一交点B(异于点A),求证:PF平分![]() .
.
19. 已知数列![]() 是等差数列,
是等差数列,![]() 是等比数列,
是等比数列,![]() .
.
(1)求![]() ,
,![]()
![]() 通项公式;
通项公式;
(2)![]() ,
,![]() ,有
,有![]() ,
,
(i)求证:对任意实数![]() ,均有
,均有![]() ;
;
(ii)求![]() 所有元素之和.
所有元素之和.
20. 已知函数![]()
(1)![]() 时,求
时,求![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)![]() 有3个零点,
有3个零点,![]() 且
且![]() .
.
(i)求a的取值范围;
(ii)证明![]() .
.
参考答案
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的
【1题答案】
【答案】D
【2题答案】
【答案】A
【3题答案】
【答案】D
【4题答案】
【答案】C
【5题答案】
【答案】B
【6题答案】
【答案】C
【7题答案】
【答案】B
【8题答案】
【答案】A
【9题答案】
【答案】A
第Ⅱ卷(非选择题)
注意事项:
1.用黑色墨水的钢笔或签字笔将答案写在答题卡上.
2.本卷共11小题,共105分.
二、填空题:本大题共6个小题,每小题5分,共30分.
【10题答案】
【答案】![]()
【11题答案】
【答案】![]()
【12题答案】
【答案】2
【13题答案】
【答案】 ①. ![]() ②.
②. ![]()
【14题答案】
【答案】 ①. ![]() ; ②.
; ②. ![]()
【15题答案】
【答案】![]()
三、解答题:本大题共5小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本题满分14分)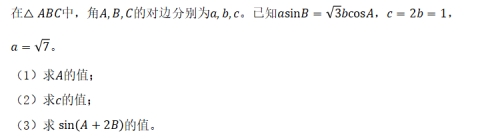
【答案】(1)![]()
(2)c=3
(3)![]()
【分值】14
17.(本题满分15分)


【答案】

(2)![]()
(3)![]()
【分值】15
18.(本题满分15分) 已知椭圆![]() 的左焦点为F,右顶点为
的左焦点为F,右顶点为![]() 为
为![]() 上一点,且直线
上一点,且直线![]() 的斜率为
的斜率为![]() ,
,![]() 的面积为
的面积为![]() ,离心率为
,离心率为![]() 。
。
(1)求椭圆的方程;
(2)过点P的直线与椭圆有唯一交点B(异于点A),求证:![]() 。
。
【答案】(1)![]()


【分值】15
19.(本题满分15分) ![]() 是等差数列,
是等差数列,![]() 是等比数列,
是等比数列,![]()
![]()
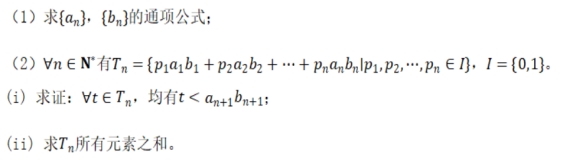
【答案】(1)![]()
(2)

(ii)![]()
【分值】15
20.(本题满分16分)已知函数![]() .
.
(1)a=1时,求f(x)在点(1,f(1))处的切线方程;
(2)f(x)有![]() 个零点
个零点![]() ,且
,且![]() .
.
(i)求![]() 的取值范围;
的取值范围;
(ii)证明:![]()
【答案】(1)y=x
(2)(i)![]()



【分值】16
