2024年黑龙江省大庆市中考数学真题及答案
一、选择题:本题10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合要求.
1. 下列各组数中,互为相反数的是( )
A. ![]() 和
和![]() B. 2024和
B. 2024和![]()
C. ![]() 和2024 D.
和2024 D. ![]() 和
和![]()
【答案】A
2. 人体内一种细胞的直径约为1.56微米,相当于0.00000156米,数字0.00000156用科学记数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
3. 垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
【答案】D
4. 下列常见的几何体中,主视图和左视图不同的是( )
A. 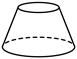 B.
B. 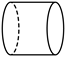
C. 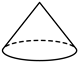 D.
D. 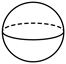
【答案】B
5. “铁人王进喜纪念馆”“龙凤湿地公园”“滨水绿道”和“数字大庆中心”是大庆市四个有代表性的旅游景点.若小娜从这四个景点中随机选择两个景点游览,则这两个景点中有“铁人王进喜纪念馆”的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
6. 下列说法正确的是( )
A. 若![]() ,则
,则![]()
B. 一件衣服降价20%后又提价20%,这件衣服的价格不变
C. 一个锐角和一条边分别相等的两个直角三角形全等
D. 若一个多边形的内角和是外角和的2倍,则这个多边形是六边形
【答案】D
7. 如图,在一次综合实践课上,为检验纸带①、②的边线是否平行,小庆和小铁采用了两种不同的方法:小庆把纸带①沿![]() 折叠,量得
折叠,量得![]() ;小铁把纸带②沿
;小铁把纸带②沿![]() 折叠,发现
折叠,发现![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合.且点C,G,D在同一直线上,点E,H,F也在同一直线上.则下列判断正确的是( )
重合.且点C,G,D在同一直线上,点E,H,F也在同一直线上.则下列判断正确的是( )
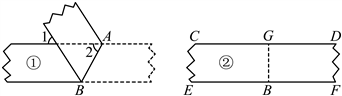
A. 纸带①、②的边线都平行
B. 纸带①、②的边线都不平行
C. 纸带①的边线平行,纸带②的边线不平行
D. 纸带①的边线不平行,纸带②的边线平行
【答案】D
8. 在同一平面直角坐标系中,函数![]() 与
与![]() 的大致图象为( )
的大致图象为( )
A. 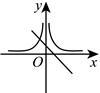 B.
B. 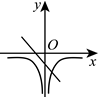
C. 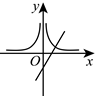 D.
D. 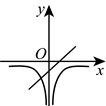
【答案】C
9. 小庆、小铁、小娜、小萌四名同学均从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A. 小庆选出四个数字的方差等于![]() B. 小铁选出四个数字的方差等于
B. 小铁选出四个数字的方差等于![]()
C. 小娜选出四个数字的平均数等于![]() D. 小萌选出四个数字的极差等于
D. 小萌选出四个数字的极差等于![]()
【答案】A
10. 如图,在矩形![]() 中,
中,![]() ,
,![]() ,点M是
,点M是![]() 边的中点,点N是
边的中点,点N是![]() 边上任意一点,将线段
边上任意一点,将线段![]() 绕点M顺时针旋转
绕点M顺时针旋转![]() ,点N旋转到点
,点N旋转到点![]() ,则
,则![]() 周长的最小值为( )
周长的最小值为( )
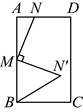
A. 15 B. ![]() C.
C. ![]() D. 18
D. 18
【答案】B
二、填空题:本题8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.
11. 计算:![]() =___.
=___.
【答案】﹣2
12. 已知![]() ,则
,则![]() 的值是___________.
的值是___________.
【答案】3
13. 如图所示,一个球恰好放在一个圆柱形盒子里,记球的体积为![]() ,圆柱形盒子的容积为
,圆柱形盒子的容积为![]() ,则
,则![]() ______.(球体体积公式:
______.(球体体积公式:![]() ,其中r为球体半径)
,其中r为球体半径)
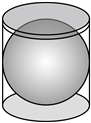
【答案】![]()
14. 请写出一个过点![]() 且y的值随x值增大而减小的函数的解析式 _____.
且y的值随x值增大而减小的函数的解析式 _____.
【答案】![]() (答案不唯一)
(答案不唯一)
15. 不等式组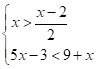 的整数解有______个.
的整数解有______个.
【答案】![]()
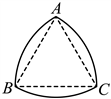
16. 如图所示的曲边三角形也称作“莱洛三角形”,它可以按下述方法作出:作等边三角形![]() ;分别以点
;分别以点![]() ,
,![]() ,
,![]() 为圆心,以
为圆心,以![]() 的长为半径作
的长为半径作![]() ,
,![]() ,
,![]() .三段弧所围成的图形就是一个曲边三角形.若该“莱洛三角形”的周长为
.三段弧所围成的图形就是一个曲边三角形.若该“莱洛三角形”的周长为![]() ,则它的面积是______.
,则它的面积是______.
【答案】![]()
17. 如图①,直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为______.

【答案】48
18. 定义:若一个函数图象上存在纵坐标是横坐标2倍的点,则把该函数称为“倍值函数”,该点称为“倍值点”.例如:“倍值函数”![]() ,其“倍值点”为
,其“倍值点”为![]() .下列说法不正确的序号为______.
.下列说法不正确的序号为______.
①函数![]() 是“倍值函数”;
是“倍值函数”;
②函数![]() 的图象上的“倍值点”是
的图象上的“倍值点”是![]() 和
和![]() ;
;
③若关于x的函数![]() 的图象上有两个“倍值点”,则m的取值范围是
的图象上有两个“倍值点”,则m的取值范围是![]() ;
;
④若关于x的函数![]() 的图象上存在唯一的“倍值点”,且当
的图象上存在唯一的“倍值点”,且当![]() 时,n的最小值为k,则k的值为
时,n的最小值为k,则k的值为![]() .
.
【答案】①③④
三、解答题:本题10小题,共66分.请在答题卡指定区域内作答,解答应写出必要的文字说明、计算过程、证明过程.
19. 求值:![]() .
.
【答案】1
20. 先化简,再求值:![]() ,其中
,其中![]() .
.
【答案】![]() ,
,![]()
21. 为了健全分时电价机制,引导电动汽车在用电低谷时段充电,某市实施峰谷分时电价制度,用电高峰时段(简称峰时):7:00—23:00,用电低谷时段(简称谷时):23:00—次日7:00,峰时电价比谷时电价高![]() 元/度.市民小萌的电动汽车用家用充电桩充电,某月的峰时电费为50元,谷时电费为30元,并且峰时用电量与谷时用电量相等,求该市谷时电价.
元/度.市民小萌的电动汽车用家用充电桩充电,某月的峰时电费为50元,谷时电费为30元,并且峰时用电量与谷时用电量相等,求该市谷时电价.
【答案】该市谷时电价![]() 元/度
元/度
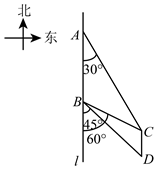
22. 如图,![]() 是一座南北走向的大桥,一辆汽车在笔直的公路
是一座南北走向的大桥,一辆汽车在笔直的公路![]() 上由北向南行驶,在
上由北向南行驶,在![]() 处测得桥头
处测得桥头![]() 在南偏东
在南偏东![]() 方向上,继续行驶
方向上,继续行驶![]() 米后到达
米后到达![]() 处,测得桥头
处,测得桥头![]() 在南偏东
在南偏东![]() 方向上,桥头
方向上,桥头![]() 在南偏东
在南偏东![]() 方向上,求大桥
方向上,求大桥![]() 的长度.(结果精确到
的长度.(结果精确到![]() 米,参考数据:
米,参考数据:![]() )
)
【答案】![]() 米
米
23. 根据教育部制定的《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织学生参加了国防知识竞赛,将学生的百分制成绩(x分)用5级记分法呈现:“![]() ”记为1分,“
”记为1分,“![]() ”记为2分,“
”记为2分,“![]() ”记为3分,“
”记为3分,“![]() ”记为4分,“
”记为4分,“![]() ”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制统计图表,部分信息如下:
”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制统计图表,部分信息如下:
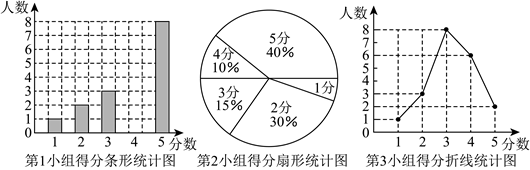
平均数 | 中位数 | 众数 | |
第1小组 | 3.9 | 4 | a |
第2小组 | b | 3.5 | 5 |
第3小组 | 3.25 | c | 3 |
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角为______度;
②请补全第1小组得分条形统计图;
(2)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生竞赛成绩不低于90分?
【答案】(1)①18;②
(2)5;![]() ;3
;3
(3)估计该校约有![]() 名学生竞赛成绩不低于90分.
名学生竞赛成绩不低于90分.
24. 如图,平行四边形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 的平分线,且E、F分别在边
的平分线,且E、F分别在边![]() ,
,![]() 上
上
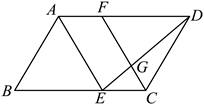
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)见解析 (2)![]() .
.
【解析】
【小问1详解】
证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∵![]() 分别是
分别是![]() 、
、![]() 的平分线,
的平分线,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
25. “尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的![]() 天中,第
天中,第![]() 天
天![]() 且
且![]() 为整数)的售价为
为整数)的售价为![]() (元
(元![]() 千克).当
千克).当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .销量
.销量![]() (千克)与
(千克)与![]() 的函数关系式为
的函数关系式为![]() ,已知该产品第
,已知该产品第![]() 天的售价为
天的售价为![]() 元
元![]() 千克,第
千克,第![]() 天的售价为
天的售价为![]() 元
元![]() 千克,设第
千克,设第![]() 天的销售额为
天的销售额为![]() (元).
(元).
(1)![]() ,
,![]() _____;
_____;
(2)写出第![]() 天的销售额
天的销售额![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求在试销售的![]() 天中,共有多少天销售额超过
天中,共有多少天销售额超过![]() 元?
元?
【答案】(1)![]() ,
,![]()
(2)
(3)在试销售的的天销售额超过![]() 元
元
26. 如图1,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上,点B,C在第一象限,四边形![]() 是平行四边形,点C在反比例函数
是平行四边形,点C在反比例函数![]() 的图象上,点C的横坐标为2,点B的纵坐标为3.
的图象上,点C的横坐标为2,点B的纵坐标为3.
提示:在平面直角坐标系中,若两点分别为![]() ,
,![]() ,则
,则![]() 中点坐标为
中点坐标为![]() .
.
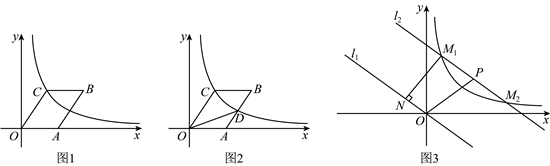
(1)求反比例函数的表达式;
(2)如图2,点D是![]() 边的中点,且在反比例函数
边的中点,且在反比例函数![]() 图象上,求平行四边形
图象上,求平行四边形![]() 的面积;
的面积;
(3)如图3,将直线![]() 向上平移6个单位得到直线
向上平移6个单位得到直线![]() ,直线
,直线![]() 与函数
与函数![]() 图象交于
图象交于![]() ,
,![]() 两点,点P为
两点,点P为![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点N.请直接写出P点坐标和
于点N.请直接写出P点坐标和![]() 的值.
的值.
【答案】
(1)![]()
(2)9
(3)![]()
27. 如图,![]() 为为在为,两线相交于点
为为在为,两线相交于点![]() ,过点
,过点![]() 作为
作为
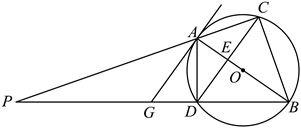
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() .求
.求![]() 的值.
的值.
【答案】
(1)见解析 (2)见解析
(3)![]()
【解析】
【小问1详解】
证明:∵将![]() 沿直线
沿直线![]() 翻折到
翻折到![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的直径,
的直径,![]() 是切线,
是切线,
∴![]() ,
,
∴![]() ;
;
【小问2详解】
解:∵![]() 是切线,
是切线,
∴![]() ,
,
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∵由折叠可得![]() ,
,
∴![]() ,
,
∵四边形![]() 是
是![]() 的内接四边形,
的内接四边形,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ;
;
28. 如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.![]() 点坐标为
点坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点,点
为抛物线顶点,点![]() 为
为![]() 中点.
中点.
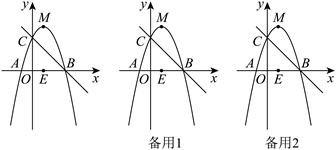
(1)求二次函数的表达式;
(2)在直线![]() 上方的抛物线上存在点
上方的抛物线上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知![]() ,
,![]() 为抛物线上不与
为抛物线上不与![]() ,
,![]() 重合的相异两点.
重合的相异两点.
①若点![]() 与点
与点![]() 重合,
重合,![]() ,且
,且![]() ,求证:
,求证:![]() ,
,![]() ,
,![]() 三点共线;
三点共线;
②若直线![]() ,
,![]() 交于点
交于点![]() ,则无论
,则无论![]() ,
,![]() 在抛物线上如何运动,只要
在抛物线上如何运动,只要![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,
,![]() ,
,![]() 中必存在面积为定值的三角形.请直接写出其中面积为定值的三角形及其面积,不必说明理由
中必存在面积为定值的三角形.请直接写出其中面积为定值的三角形及其面积,不必说明理由
【答案】(1)![]()
(2)![]()
(3)①见解析;②![]() 的面积为定值
的面积为定值![]()
【解析】
【小问3详解】
①点![]() 与点
与点![]() 重合,则
重合,则![]() ,
,
∵点![]() 为
为![]() 中点,
中点,![]() ,
,![]()
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,代入
,代入![]() ,
,![]()
∴![]()
解得:![]()
∴![]()
联立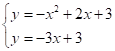
解得:![]() 或
或![]()
∴![]() ,在直线
,在直线![]() 上
上
即![]() ,
,![]() ,
,![]() 三点共线;
三点共线;
