2024年辽宁中考数学试题及答案
第一部分 选择题（共30分）
一、选择题（本题共10小题，每小题3分，共30分．在每小题给出的四个选项中；有一项是符合题目要求的）
1．如图是由5个相同的小立方块搭成的几何体，这个几何体的俯视图是（ ）
A．
B．
C．
D．
2．亚洲、欧洲、非洲和南美洲的最低海拔如下表：
大洲 | 亚洲 | 欧洲 | 非洲 | 南美洲 |
最低海拔 |
|
|
|
|
其中最低海拔最小的大洲是（ ）
A．亚洲 B．欧洲 C．非洲 D．南美洲
3．越山向海，一路花开．在5月24日举行的2024辽宁省高品质文体旅融合发展大型产业招商推介活动中，全省30个重大文体旅项目进行集中签约，总金额达532亿元．将53200000000用科学记数法表示为（ ）
A．
B．
C．
D．
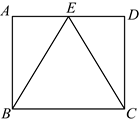
4．如图，在矩形
中，点
在
上，当
是等边三角形时，
为（ ）
A．
B．
C．
D．
5．下列计算正确的是（ ）
A．
B．
C．
D．
6．一个不透明袋子中装有4个白球，3个红球，2个绿球，1个黑球，每个球除颜色外都相同．从中随机摸出一个球，则下列事件发生的概率为
的是（ ）
A．摸出白球 B．摸出红球 C．摸出绿球 D．摸出黑球
7．纹样是我国古代艺术中的瑰宝．下列四幅纹样图形既是轴对称图形又是中心对称图形的是（ ）
A．
B．
C．
D．
8．我国古代数学著作《孙子算经》中有“雉兔同笼”问题：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”其大意是：鸡兔同笼，共有35个头，94条腿，问鸡兔各多少只？设鸡有
只，兔有
只，根据题意可列方程组为（ ）
A．
B．
C．
D．
9．如图，
的对角线
，
相交于点
，
，
，若
，
，则四边形
的周长为（ ）
A．4 B．6 C．8 D．16
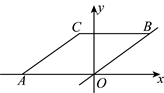
10．如图，在平面直角坐标系是在
轴负半轴上，顶点
在直线
上，若点的横坐标是8，为点
的坐标为（ ）
A．
B．
C．
D．
第二部分 非选择题（共90分）
二、填空题（本题共5小题，每小题3分，共15分）
11．方程
的解为 ．
12．在平面直角坐标系中，线段
的端点坐标分别为是的对应点
的坐标为
，则点的对应点
的坐标为 ．
13．如图，
，
与
相交于点
，且
与
的面积比是
，若
，则
的长为 ．
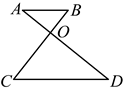
14．如图，在平面直角坐标系中，抛物线
与与相交于点
，，点的坐标为
，若点
在抛物线上，则的长为 ．
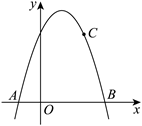
15．如图，四边形
中，
，
，
，
．以点
为圆心，以
长为半径作图，与
相交于点
，连接
．以点为圆心，适当长为半径作弧，分别与
，
相交于点
，
，再分别以点，为圆心，大于
的长为半径作弧，两弧在
的内部相交于点
，作射线
，与
相交于点
，则
的长为 （用含
的代数式表示）．
三、解答题（本题共8小题，共75分．解答应写出文字说明、演算步骤或推理过程）
16．（1）计算：
；
（2）计算：
．
17．甲、乙两个水池注满水，蓄水量均为
、工作期间需同时排水，乙池的排水速度是
．若排水3h，则甲池剩余水量是乙池剩余水量的2倍．
(1)求甲池的排水速度．
(2)工作期间，如果这两个水池剩余水量的和不少于
，那么最多可以排水几小时？
18．某校为了解七年级学生对消防安全知识掌握的情况，随机抽取该校七年级部分学生进行测试，并对测试成绩进行收集、整理、描述和分析（测试满分为100分，学生测试成绩
均为不小于60的整数，分为四个等级：D：
，C：
，B：
，A：
），部分信息如下：
信息一：
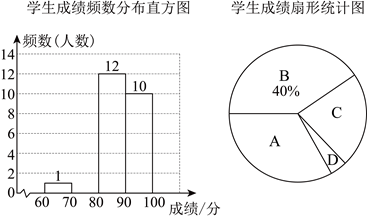
信息二：学生成绩在B等级的数据（单位：分）如下：
80，81，82，83，84，84，84，86，86，86，88，89
请根据以上信息，解答下列问题：
(1)求所抽取的学生成组为C等级的人数；
(2)求所抽取的学生成绩的中位数；
(3)该校七年级共有360名学生，若全年级学生都参加本次测试，请估计成绩为A等级的人数．
19．某商场出售一种商品，经市场调查发现，日销售量
（件）与每件售价
（元）满足一次函数关系，部分数据如下表所示：
每件售价 |
|
|
|
|
|
日销售量 |
|
|
|
|
|
(1)求与之间的函数关系式（不要求写出自变量的取值范围）；
(2)该商品日销售额能否达到
元？如果能，求出每件售价：如果不能，请说明理由．
20．如图1，在水平地面上，一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起．起始位置示意图如图2，此时测得点
到
所在直线的距离
，
；停止位置示意图如图3，此时测得
（点
，，
在同一直线上，且直线
与平面平行，图3中所有点在同一平面内．定滑轮半径忽略不计，运动过程中绳子总长不变．（参考数据：
，
，
，
）
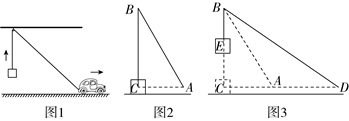
(1)求
的长；
(2)求物体上升的高度
（结果精确到
）．
21．如图，
是
的外接圆，是的直径，点
在
上，
，
在
的延长线上，
．
(1)如图1，求证：是的切线；
(2)如图2，若
，
，求
的长．
22．如图，在中，
，
．将线段
绕点
顺时针旋转
得到线段
，过点作
，垂足为．
图1 图2 图3
(1)如图1，求证：
；
(2)如图2，
的平分线与
的延长线相交于点
，连接
，的延长线与
的延长线相交于点
，猜想
与
的数量关系，并加以证明；
(3)如图3，在（2）的条件下，将
沿
折叠，在
变化过程中，当点落在点
的位置时，连接
．
①求证：点是的中点；
②若
，求
的面积．
23．已知
是自变量
的函数，当
时，称函数
为函数的“升幂函数”．在平面直角坐标系中，对于函数图象上任意一点的“关于的升幂点”，点
在函数的“升幂函数”的图象上．例如：函数
，当
时，则函数
是函数的“升幂函数”．在平面直角坐标系中，函数的图象上任意一点是“关于的升幂点”，点在函数的“升幂函数”的图象上．
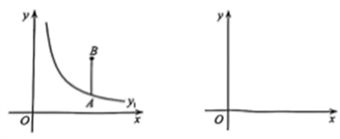
图1 图2
(1)求函数
的“升幂函数”
的函数表达式；
(2)如图1，点
在函数
的图象上，点“关于
的升幂点”
在点上方，当
时，求点的坐标；
(3)点在函数
的图象上，点“关于的升幂点”为点，设点的横坐标为
．
①若点与点重合，求的值；
②若点在点的上方，过点作
轴的平行线，与函数的“升幂函数”的图象相交于点
，以
，
为邻边构造矩形
，设矩形的周长为
，求关于的函数表达式；
③在②的条件下，当直线
与函数的图象的交点有3个时，从左到右依次记为
，
，
，当直线
与函数的图象的交点有2个时，从左到右依次记为
，
，若
，请直接写出
的值
参考答案
1．A
2．A
3．C
4．C
5．D
6．B
7．B
8．D
9．C
10．B
11．
12．
13．12
14．
15．
16．（1）
；（2）1
17．(1)
(2)4小时
18．(1)7人
(2)85
(3)120人
19．(1)
；
(2)该商品日销售额不能达到
元。
20．(1)
(2)
21．(1)见详解
(2)
【详解】（1）证明：连接
，
∵
，
∴
，
∴
，
∵
，
∴
，
∵
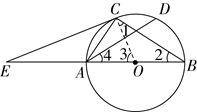
为直径，
∴
，
∴
，即
，
∵
，
∴
，
∴
，
∴
，
∴
，
∴
是
的切线；
22．(1)见详解
(2)
(3)30
【详解】（1）证明：如图，
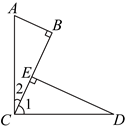
由题意得，
，
∴
∵
，
∴
，
∴
，
∴
，
∵
，
∴
，
∴
；
23．(1)
(2)
(3)①
或
；②
；③
或