2023年辽宁沈阳中考数学试题及答案
一、选择题(本大题共10小题,共20)
1.2的相反数是( )
A.2 B.-2 C.![]() D.
D.![]()
2.如图是由![]() 个相同的小立方块搭成的几何体,这个几何体的主视图是( )
个相同的小立方块搭成的几何体,这个几何体的主视图是( )
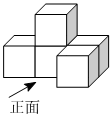
A.![]() B.
B.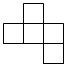 C.
C.![]() D.
D.![]()
3.我国自主研发的![]() 口径球面射电望远镜(
口径球面射电望远镜(![]() )有“中国天眼”之称,它的反射面面积约为
)有“中国天眼”之称,它的反射面面积约为![]() 用科学记数法表示数据
用科学记数法表示数据![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列计算结果正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.不等式![]() 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.某班级准备利用暑假去研学旅行,他们准备定做一批容量一致的双肩包![]() 为此,活动负责人征求了班内同学的意向,得到了如下数据:
为此,活动负责人征求了班内同学的意向,得到了如下数据:
|
容量 |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
则双肩包容量的众数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.下列说法正确的是( )
A.将油滴入水中,油会浮在水面上是不可能事件
B.抛出的篮球会下落是随机事件
C.了解一批圆珠笔芯的使用寿命,采用普查的方式
D.若甲、乙两组数据的平均数相同,![]() ,
,![]() ,则甲组数据较稳定
,则甲组数据较稳定
8.已知一次函数![]() 的图象如图所示,则
的图象如图所示,则![]() ,
,![]() 的取值范围是( )
的取值范围是( )
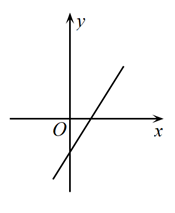
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
9.二次函数![]() 图象的顶点所在的象限是( )
图象的顶点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
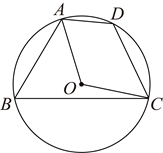
10.如图,四边形![]() 内接于
内接于![]() ,
,![]() 的半径为
的半径为![]() ,
,![]() ,则
,则![]() 的长是( )
的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共6小题,共18分)
11.因式分解:![]() .
.
12.当![]() 时,代数式
时,代数式![]() 的值为 .
的值为 .
13.若点![]() 和点
和点![]() 都在反比例函数
都在反比例函数![]() 的图象上,则
的图象上,则![]()
![]() .(用“
.(用“![]() ”“
”“![]() ”或“
”或“![]() ”填空)
”填空)
14.如图,直线![]() ,直线
,直线![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,小明同学利用尺规按以下步骤作图:
,小明同学利用尺规按以下步骤作图:
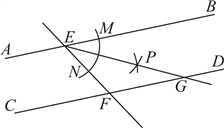
(1)点![]() 为圆心,以任意长为半径作弧交射线
为圆心,以任意长为半径作弧交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ;
;
(2)分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 内交于点
内交于点![]() ;
;
(3)作射线![]() 交直线
交直线![]() 于点
于点![]() ;若
;若![]() ,则
,则![]() 度.
度.
15.如图,王叔叔想用长为![]() 的栅栏,再借助房屋的外墙围成一个矩形羊圈
的栅栏,再借助房屋的外墙围成一个矩形羊圈![]() ,已知房屋外墙足够长,当矩形
,已知房屋外墙足够长,当矩形![]() 的边
的边![]()
![]() 时,羊圈的面积最大.
时,羊圈的面积最大.

16.如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的长为 .
的长为 .
三、解答题(本大题共9小题,共82)
17.计算:![]() .
.
18.为弘扬中华优秀传统文化,学校举办“经典诵读”比赛,将比赛内容分为“唐诗”“宋词”“元曲”三类(分别用![]() ,
,![]() ,
,![]() 依次表示这三类比赛内容).现将正面写有
依次表示这三类比赛内容).现将正面写有![]() ,
,![]() ,
,![]() 的三张完全相同的卡片背面朝上洗匀,由选手抽取卡片确定比赛内容
的三张完全相同的卡片背面朝上洗匀,由选手抽取卡片确定比赛内容![]() 选手小明先从三张卡片中随机抽取一张,记下字母后放回洗匀,选手小梅再随机抽取一张,记下字母
选手小明先从三张卡片中随机抽取一张,记下字母后放回洗匀,选手小梅再随机抽取一张,记下字母![]() 请用画树状图或列表的方法,求小明和小梅抽到同一类比赛内容的概率.
请用画树状图或列表的方法,求小明和小梅抽到同一类比赛内容的概率.
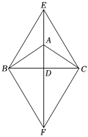
19.如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 、
、![]() ,求证:四边形
,求证:四边形![]() 是菱形.
是菱形.
20.“书香润沈城,阅读向未来”,沈阳市第十五届全民读书季启动之际![]() 某中学准备购进一批图书供学生阅读,为了合理配备各类图书,从全体学生中随机抽取了部分学生进行了问卷调查
某中学准备购进一批图书供学生阅读,为了合理配备各类图书,从全体学生中随机抽取了部分学生进行了问卷调查![]() 问卷设置了五种选项:
问卷设置了五种选项:![]() “艺术类”,
“艺术类”,![]() “文学类”,
“文学类”,![]() “科普类”,
“科普类”,![]() “体育类”,
“体育类”,![]() “其他类”,每名学生必须且只能选择其中最喜爱的一类图书,将调查结果整理绘制成如下两幅不完整的统计图.
“其他类”,每名学生必须且只能选择其中最喜爱的一类图书,将调查结果整理绘制成如下两幅不完整的统计图.
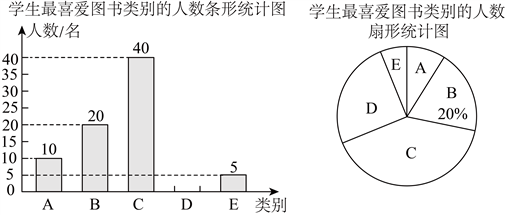
根据以上信息,解答下列问题:
(1)此次被调查的学生人数为______ 名;
(2)请直接补全条形统计图;
(3)在扇形统计图中,![]() “艺术类”所对应的圆心角度数是______ 度;
“艺术类”所对应的圆心角度数是______ 度;
(4)据抽样调查结果,请你估计该校![]() 名学生中,有多少名学生最喜爱
名学生中,有多少名学生最喜爱![]() “科普类”图书.
“科普类”图书.
21.甲、乙两人加工同一种零件,每小时甲比乙多加工![]() 个这种零件,甲加工
个这种零件,甲加工![]() 个这种零件所用的时间与乙加工
个这种零件所用的时间与乙加工![]() 个这种零件所用的时间相等,求乙每小时加工多少个这种零件.
个这种零件所用的时间相等,求乙每小时加工多少个这种零件.
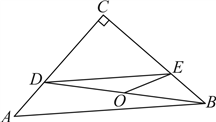
22.如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上的一点(点
上的一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() 、
、![]() ,点
,点![]() 是
是![]() 上的一点,
上的一点,![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() .
.
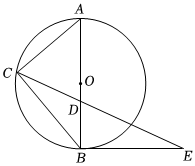
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为
的半径为![]() ,
,![]() ,则
,则![]() 的长为______ .
的长为______ .
23.如图,在平面直角坐标系中,一次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() 直线
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() 点
点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() 设点
设点![]() 的横坐标为
的横坐标为![]()
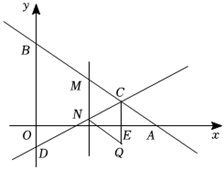
(1)求![]() 的值和直线
的值和直线![]() 的函数表达式;
的函数表达式;
(2)以线段![]() ,
,![]() 为邻边作?
为邻边作?![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
①当![]() 时,设线段
时,设线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 之间的关系式;
之间的关系式;
②连接![]() ,
,![]() ,当
,当![]() 的面积为
的面积为![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
24.如图![]() ,在
,在![]() 纸片中,
纸片中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一点(点
边上的一点(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() ,将
,将![]() 纸片沿
纸片沿![]() 所在直线折叠,点
所在直线折叠,点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,射线
,射线![]() 与射线
与射线![]() 交于点
交于点![]() .
.
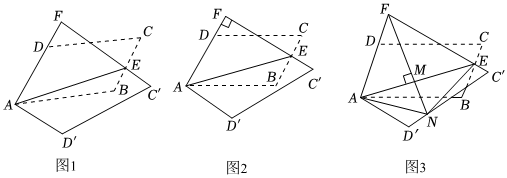
(1)求证:![]() ;
;
(2)如图![]() ,当
,当![]() 时,
时,![]() 的长为______ ;
的长为______ ;
(3)如图![]() ,当
,当![]() 时,过点
时,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
25.如图,在平面直角坐标系中,二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴的交点为点
轴的交点为点![]() 和点
和点![]() .
.
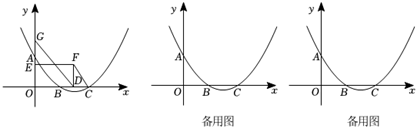
(1)求这个二次函数的表达式;
(2)点![]() ,
,![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 以线段
以线段![]() ,
,![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() ,设
,设![]() .
.
![]() 连接
连接![]() ,当
,当![]() 与
与![]() 相似时,求
相似时,求![]() 的值;
的值;
![]() 当点
当点![]() 与点
与点![]() 重合时,将线段
重合时,将线段![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 后得到线段
后得到线段![]() ,连接
,连接![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后得到
后得到![]() ,点
,点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,连接
,连接![]() 当
当![]() 的边与线段
的边与线段![]() 垂直时,请直接写出点
垂直时,请直接写出点![]() 的横坐标.
的横坐标.
参考答案
1.B
2.A
3.D
4.D
5.A
6.C
7.D
8.A
9.B
10.C
11.a(a+1)2
12.2
13.![]()
14.58
15.15
16.![]() 或
或![]()
17.10
18.图见解析,![]()
【详解】解:用树状图法表示所有等可能出现的结果如下:
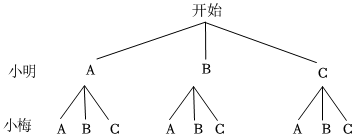
共有![]() 种等可能出现的结果,其中小明和小梅抽到同一类比赛内容的有
种等可能出现的结果,其中小明和小梅抽到同一类比赛内容的有![]() 种,
种,
所以小明和小梅抽到同一类比赛内容的概率为![]() .
.
19.证明见解析
【详解】证明:![]() ,
,![]() 是
是![]() 边上的中线,
边上的中线,
![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
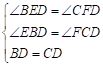 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是菱形.
是菱形.
20.(1)100
(2)见解析
(3)36
(4)720名
【详解】
(2)![]() 类的人数为:
类的人数为:![]() 名
名![]() ,
,
补全条形统计图如下:
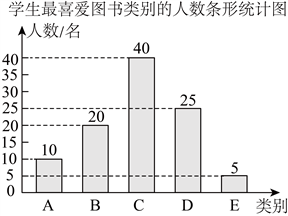 ;
;
21.乙每小时加工![]() 个这种零件.
个这种零件.
22.(1)证明:![]() 是
是![]() 的直径,
的直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
![]() 为
为![]() 的直径,
的直径,
![]() 是
是![]() 的切线;
的切线;
(2)8
23.(1)![]() ,
,![]()
(2)①![]() ;②
;②![]()
24.
(1)证明:![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() ,
,
由折叠性质可知,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
25.(1)![]()
(2)①![]() 或
或![]() ;②
;②![]() 或
或![]() 或
或![]()
(2)![]() ;
;
(3)![]()
