2023年辽宁本溪中考数学试题及答案
第一部分 选择题
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 2的绝对值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
2. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B. 
C.  D.
D. 
3. 如图所示,该几何体的俯视图是( )
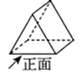
A. 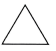 B.
B. 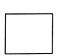 C.
C.  D.
D. 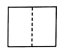
4. 下列运算正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 在一次中学生田径运动会上,参加男子跳高的10名运动员的成绩如下表所示:
成绩/m | 1.40 | 1.50 | 1.60 | 170 | 1.80 |
人数/名 | 1 | 3 | 2 | 3 | 1 |
则这10名运动员成绩的中位数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 如图,直线![]() 被射线
被射线![]() 所截,
所截,![]() ,若
,若![]() °,则
°,则![]() 的度数为( )
的度数为( )
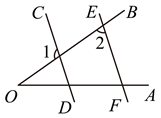
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 下列调查中,适宜采用全面调查方式的是( )
A. 了解某种灯泡的使用寿命
B. 了解一批冷饮的质量是否合格
C. 了解全国八年级学生的视力情况
D. 了解某班同学中哪个月份出生的人数最多
8. 某校八年级学生去距离学校![]() 的游览区游览,一部分学生乘慢车先行,出发
的游览区游览,一部分学生乘慢车先行,出发![]() 后,另一部分学生乘快车前往,结果他们同时到达.已知快车的速度是慢车速度的
后,另一部分学生乘快车前往,结果他们同时到达.已知快车的速度是慢车速度的![]() 倍,求慢车的速度,设慢车的速度是
倍,求慢车的速度,设慢车的速度是![]() ,所列方程正确的是( )
,所列方程正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
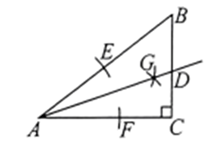
9. 如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,适当长为半径作弧,分别交
为圆心,适当长为半径作弧,分别交![]() 于点
于点![]() ,分别以点
,分别以点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 的内部相交于点
的内部相交于点![]() ,作射线
,作射线![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
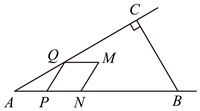
10. 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿射线
的速度沿射线![]() 匀速运动,到点
匀速运动,到点![]() 停止运动,同时动点
停止运动,同时动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿射线
的速度沿射线![]() 匀速运动.当点
匀速运动.当点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.在
也随之停止运动.在![]() 的右侧以
的右侧以![]() 为边作菱形
为边作菱形![]() ,点
,点![]() 在射线
在射线![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() ,菱形
,菱形![]() 与
与![]() 的重叠部分的面积为
的重叠部分的面积为![]() ,则能大致反映
,则能大致反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
A. 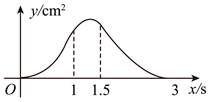 B.
B. 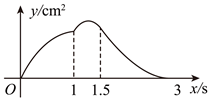
C. 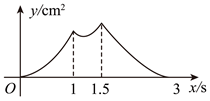 D.
D. 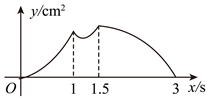
第二部分 非选择题(共120分)
二、填空题(本题共8小题,每小题3分,共24分)
11. 截止到2023年4月底,我国![]() 网络覆盖全国所有地级(以上)市、县城城区,
网络覆盖全国所有地级(以上)市、县城城区,![]() 移动电话用户达到
移动电话用户达到![]() 户,将数据
户,将数据![]() 用科学记数法表示为___________.
用科学记数法表示为___________.
12. 分解因式:![]() __.
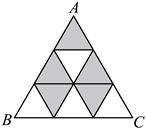
__.
13. 如图,等边三角形![]() 是由9个大小相等的等边三角形构成,随机地往
是由9个大小相等的等边三角形构成,随机地往![]() 内投一粒米,落在阴影区域的概率为___________.
内投一粒米,落在阴影区域的概率为___________.
14. 若关于x的一元二次方程![]() 有两个不相等的实数根,则k的取值范围是_____.
有两个不相等的实数根,则k的取值范围是_____.
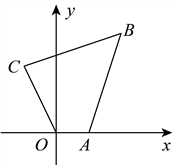
15. 如图,在平面直角坐标系中,四边形![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,若四边形
,若四边形![]() 与四边形
与四边形![]() 关于原点
关于原点![]() 位似,且四边形
位似,且四边形![]() 的面积是四边形
的面积是四边形![]() 面积的4倍,则第一象限内点
面积的4倍,则第一象限内点![]() 的坐标为___________
的坐标为___________
16. 如图,矩形![]() 的边
的边![]() 平行于
平行于![]() 轴,反比例函数
轴,反比例函数![]() 的图象经过点
的图象经过点![]() ,对角线
,对角线![]() 的延长线经过原点
的延长线经过原点![]() ,且
,且![]() ,若矩形
,若矩形![]() 的面积是8,则
的面积是8,则![]() 的值为___________.
的值为___________.
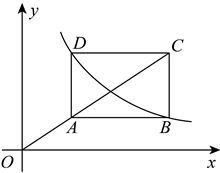
17. 如图,在三角形纸片![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点,将三角形纸片沿
上的动点,将三角形纸片沿![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,当
处,当![]() 时,
时,![]() 的度数为___________.
的度数为___________.
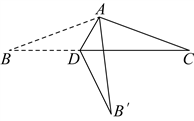
18. 如图,线段![]() ,点
,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,在
,在![]() 的上方作
的上方作![]() ,使
,使![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,当
,当![]() 最小时,
最小时,![]() 的面积为___________.
的面积为___________.

三、解答题(第19题10分,第20题12分,共22分)
19. 先化简,再求值:![]() ,其中
,其中![]()
20. 6月5日是世界环境日,为提高学生的环保意识,某校举行了环保知识竞赛,从全校学生的成绩中随机抽取了部分学生的成绩进行分析,把结果划分为4个等级:![]() (优秀);
(优秀);![]() (良好);
(良好);![]() (中);
(中);![]() (合格).并将统计结果绘制成如下两幅统计图.
(合格).并将统计结果绘制成如下两幅统计图.
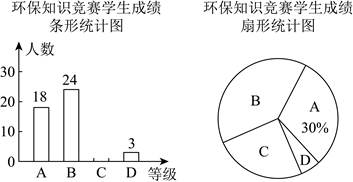
(1)本次抽样调查的学生共有___________名;
(2)补全条形统计图;
(3)该校共有1200名学生,请你估计本次竞赛获得B等级的学生有多少名?
(4)在这次竞赛中,九年级一班共有4人获得了优秀,4人中有两名男同学,两名女同学,班主任决定从这4人中随机选出2人在班级为其他同学做培训,请你用列表法或画树状图法,求所选2人恰好是一男一女的概率.
四、解答题(第21题12分,第22题12分,共24分)
21. 某礼品店经销A,B两种礼品盒,第一次购进A种礼品盒10盒,B种礼品盒15盒,共花费2800元;第二次购进A种礼品盒6盒,B种礼品盒5盒,共花费1200元
(1)求购进A,B两种礼品盒的单价分别是多少元;
(2)若该礼品店准备再次购进两种礼品盒共40盒,总费用不超过4500元,那么至少购进A种礼品盒多少盒?
22. 暑假期间,小明与小亮相约到某旅游风景区登山,需要登顶![]() 高的山峰,由山底
高的山峰,由山底![]() 处先步行
处先步行![]() 到达
到达![]() 处,再由
处,再由![]() 处乘坐登山缆车到达山顶
处乘坐登山缆车到达山顶![]() 处.已知点
处.已知点![]() ,B.D,E,F在同一平面内,山坡
,B.D,E,F在同一平面内,山坡![]() 的坡角为
的坡角为![]() ,线车行驶路线
,线车行驶路线![]() 与水平面的夹角为
与水平面的夹角为![]() (换乘登山缆车的时间忽略不计)
(换乘登山缆车的时间忽略不计)

(1)求登山缆车上升的高度![]() ;
;
(2)若步行速度为![]() ,登山缆车的速度为
,登山缆车的速度为![]() ,求从山底
,求从山底![]() 处到达山顶
处到达山顶![]() 处大约需要多少分钟(结果精确到
处大约需要多少分钟(结果精确到![]() )
)
(参考数据:![]() )
)
五、解答题(满分12分)
23. 商店出售某品牌护眼灯,每台进价为40元,在销售过程中发现,月销量![]() (台)与销售单价
(台)与销售单价![]() (元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
(元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
销售单价 | … | 50 | 60 | 70 | … |
月销量 | … | 90 | 80 | 70 | … |
(1)求y与x之间的函数关系式;
(2)当护眼灯销售单价定为多少元时,商店每月出售这种护眼灯所获的利润最大?最大月利润为多少元?
六、解答题(满分12分)
24. 如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() .
.
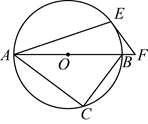
(1)求证:EF与![]() 相切;
相切;
(2)若![]() ,求
,求![]() 的长.
的长.
七、解答题(满分12分)
25. 在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上(不与点
上(不与点![]() 重合),连接
重合),连接![]() ,线段
,线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,过点
,过点![]() 作直线
作直线![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]()

(1)如图,当点![]() 与点
与点![]() 重合时,请直接写出线段
重合时,请直接写出线段![]() 与线段
与线段![]() 的数量关系;
的数量关系;
(2)如图,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() ;
;
(3)连接![]() ,
,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积记为
的面积记为![]() ,当
,当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
八、解答题(满分14分)
26. 如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
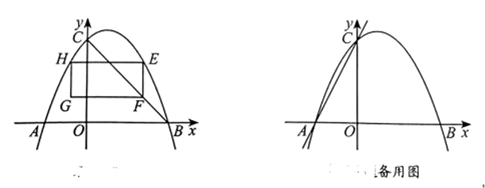
(1)求抛物线的解析式;
(2)点![]() 在第一象限内,过点
在第一象限内,过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,作
,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在点
在点![]() 的左侧,以线段
的左侧,以线段![]() 为邻边作矩形
为邻边作矩形![]() ,当矩形
,当矩形![]() 的周长为11时,求线段
的周长为11时,求线段![]() 的长;
的长;
(3)点![]() 在直线
在直线![]() 上,点
上,点![]() 在平面内,当四边形
在平面内,当四边形![]() 是正方形时,请直接写出点
是正方形时,请直接写出点![]() 的坐标.
的坐标.
参考答案
第一部分 选择题
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
【1题答案】
【答案】D
【2题答案】
【答案】A
【3题答案】
【答案】C
【4题答案】
【答案】B
【5题答案】
【答案】C
【6题答案】
【答案】C
【7题答案】
【答案】D
【8题答案】
【答案】B
【9题答案】
【答案】D
【10题答案】
【答案】A
第二部分 非选择题(共120分)
二、填空题(本题共8小题,每小题3分,共24分)
【11题答案】
【答案】![]()
【12题答案】
【答案】![]()
【13题答案】
【答案】![]()
【14题答案】
【答案】k<-![]()
【15题答案】
【答案】![]()
【16题答案】
【答案】6
【17题答案】
【答案】![]() 或
或![]()
【18题答案】
【答案】![]()
三、解答题(第19题10分,第20题12分,共22分)
【19题答案】
【答案】![]() ,5.
,5.
【20题答案】
【答案】(1)60 (2)见解析
(3)估计本次竞赛获得B等级的学生有480名;
(4)所选2人恰好是一男一女的概率为![]() .
.
四、解答题(第21题12分,第22题12分,共24分)
【21题答案】
【答案】(1)A礼品盒的单价是100元,B礼品盒的单价是120元;
(2)至少购进A种礼品盒15盒.
【22题答案】
【答案】(1)登山缆车上升的高度![]() ;
;
(2)从山底![]() 处到达山顶
处到达山顶![]() 处大约需要
处大约需要![]() .
.
五、解答题(满分12分)
【23题答案】
【答案】(1)![]()
(2)护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元
六、解答题(满分12分)
【24题答案】
【答案】(1)见解析 (2)![]() .
.
七、解答题(满分12分)
【25题答案】
【答案】(1)![]() .
.
(2)见解析. (3)![]() .
.
八、解答题(满分14分)
【26题答案】
【答案】(1)抛物线的解析式为![]() ;
;
(2)![]() ;
;
(3)点![]() 的坐标为
的坐标为![]() 或
或![]()
