2025年黑龙江大兴安岭中考数学试题及答案
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)
1.《九章算术》是我国古代著名的数学著作,在世界数学史上首次正式引入负数.若收入10元记作![]() 元,则支出+10元记作( )
元,则支出+10元记作( )
A.+10元B.-10元C.0元D.+20元
2.社会规则营造良好的社会秩序,我们要了解并遵守社会规则.下列标志是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
3.下列计算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.将一个含![]() 角的三角尺和直尺按如图摆放,若
角的三角尺和直尺按如图摆放,若![]() ,则
,则![]() 的度数是( )
的度数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.为了全面地反映物体的形状,生产实践中往往采用多个视图来反映同一物体不同方面的形状.下图中飞机的俯视图是( )

A.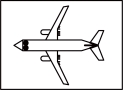 B.
B.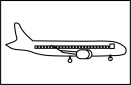 C.
C.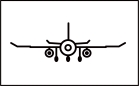 D.
D.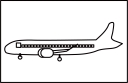
6.如果关于![]() 的分式方程
的分式方程![]() 无解,那么实数
无解,那么实数![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 且
且![]()
7.假定鸟卵孵化后,雏鸟为雌鸟与雄鸟的概率相同.如果2枚鸟卵全部成功孵化,那么2只雏鸟都是雄鸟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.神舟二十号发射窗口时间恰逢第十个“中国航天日”.为激发青少年探索浩瀚宇宙的兴趣,学校组织900名师生乘车前往航空科技馆参观,计划租用45座和60座两种客车(两种客车都要租),若每名学生都有座位且每辆客车都没有空座位,则租车方案有( )
A.3种B.4种C.5种D.6种
9.如图,在菱形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿边
出发沿边![]() 匀速运动,运动到点
匀速运动,运动到点![]() 时停止,过点
时停止,过点![]() 作
作![]() 的垂线
的垂线![]() ,在点
,在点![]() 运动过程中,垂线
运动过程中,垂线![]() 扫过菱形(即阴影部分)的面积为
扫过菱形(即阴影部分)的面积为![]() ,点
,点![]() 运动的路程为
运动的路程为![]() .下列图象能反映
.下列图象能反映![]() 与
与![]() 之间函数关系的是( )
之间函数关系的是( )

A. B.
B.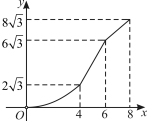 C.
C. D.
D.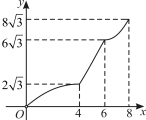
10.如图,二次函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,
,![]() ,且
,且![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 和
和![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]()
![]() 的两根,且
的两根,且![]() ,则
,则![]() ,
,![]() ;⑤关于
;⑤关于![]() 的不等式
的不等式![]()
![]() 的解集为
的解集为![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.2B.3C.4D.5
二、填空题(每小题3分,满分21分)
11.中国年水资源总量约为![]() 亿
亿![]() ,人均占有水量相当于世界人均的四分之一,居世界第110位.将
,人均占有水量相当于世界人均的四分之一,居世界第110位.将![]() 用科学记数法表示为 .
用科学记数法表示为 .
12.若代数式![]() 有意义,则实数
有意义,则实数![]() 的取值范围是 .
的取值范围是 .
13.若圆锥的底面半径为![]() ,母线长为
,母线长为![]() ,则其侧面展开图的圆心角为 度.
,则其侧面展开图的圆心角为 度.
14.如图,在![]() 中,
中,![]() ,连接
,连接![]() ,分别以点A,C为圆心,大于
,分别以点A,C为圆心,大于![]() 的长为半径作弧,两弧交于点E,F,作直线
的长为半径作弧,两弧交于点E,F,作直线![]() ,交
,交![]() 于点M,交
于点M,交![]() 于点N,若点N恰为
于点N,若点N恰为![]() 的中点,则
的中点,则![]() 的长为
的长为

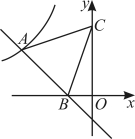
15.如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象在第二象限内交于点A,与x轴交于点B,点C坐标为
的图象在第二象限内交于点A,与x轴交于点B,点C坐标为![]() ,连接
,连接![]() ,若
,若![]() ,则实数k的值为 .
,则实数k的值为 .
16.等腰三角形纸片![]() 中,
中,![]() ,将纸片沿直线l折叠,使点A与点B重合,直线l交
,将纸片沿直线l折叠,使点A与点B重合,直线l交![]() 于点D,交直线
于点D,交直线![]() 于点E,连接
于点E,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的面积为 .
的面积为 .
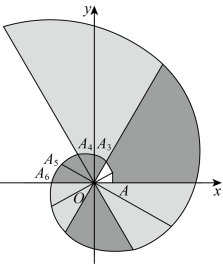
17.利用几何图形的变化可以制作出形态各异的图案.如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以
,以![]() 为边作
为边作![]() ,使
,使![]() ,
,![]() ,再以
,再以![]() 为边作
为边作![]() ,使
,使![]() ,
,![]() ,过点
,过点![]() ,
,![]() ,
,![]() 作弧
作弧![]() ,记作第1条弧;以
,记作第1条弧;以![]() 为边
为边![]() ,使
,使![]() ,
,![]() ,再以
,再以![]() 为边作
为边作![]() ,使
,使![]() ,
,![]() ,过点
,过点![]() ,
,![]() ,
,![]() 作弧
作弧![]() ,记作第2条弧……按此规律,第2025条弧上与原点
,记作第2条弧……按此规律,第2025条弧上与原点![]() 的距离最小的点的坐标为
的距离最小的点的坐标为
三、解答题(本题共7道大题,共69分)
18.(1)计算:![]()
(2)分解因式:![]()
19.解方程:![]()
20.国家卫生健康委员会宣布将2025年定为“体重管理年”,并实施为期三年的体重管理行动.某校响应号召,计划组织全校学生开展系列体育活动,筹备足球、排球、篮球、羽毛球四个球类运动的体育社团,倡导学生全员参加,为了解学生对这四项球类运动的喜爱情况,随机抽取部分学生,对其进行了“我最喜爱的球类运动项目”问卷调查(每名学生在这四项球类运动项目中选择且只能选择一项),将这部分学生的问卷进行整理,依据样本数据绘制了如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)填空:![]() __________;
__________;
(2)请补全条形统计图;
(3)扇形统计图中,“足球”对应扇形的圆心角为__________度;
(4)若该校有![]() 名学生,请你估计该校最喜爱篮球运动的学生有多少人?
名学生,请你估计该校最喜爱篮球运动的学生有多少人?
21.如图,![]() 内接于
内接于![]() ,
,![]() 为
为![]() 的直径,点D在
的直径,点D在![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,过点B作
,过点B作![]() ,交
,交![]() 于点E.
于点E.
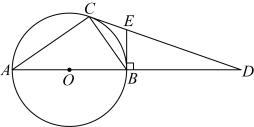
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点B是![]() 的中点,且
的中点,且![]() ,求
,求![]() 的半径.
的半径.
22.2025年春晚舞台上的机器人表演,充分演绎了科技与民族文化的完美融合.为满足学生的好奇心和求知欲,某校组织科技活动“机器人走进校园”,AI热情瞬间燃爆.校园里一条笔直的“勤学路”上依次设置了A,B,C三个互动区,机器人甲、乙分别从A,C两区同时出发开始表演,机器人甲沿“勤学路”以20米/分的速度匀速向B区行进,行至B区时停留4.5分钟(与师生热情互动)后,继续沿“勤学路”向C区匀速行进,机器人乙沿“勤学路”以10米/分的速度匀速向B区行进,行至B区时接到指令立即匀速返回,结果两机器人同时到达C区.机器人甲、乙距B区的距离y(米)与机器人乙行进的时间x(分)之间的函数关系如图所示,请结合图象信息解答下列问题:
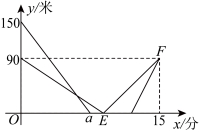
(1)A,C两区相距__________米,![]() __________;
__________;
(2)求线段![]() 所在直线的函数解析式;
所在直线的函数解析式;
(3)机器人乙行进的时间为多少分时,机器人甲、乙相距30米?(直接写出答案即可)
23.综合与实践
在探索几何图形变化的过程中,通过直观猜想、逻辑推理、归纳总结可以获得典型的几何模型,运用几何模型能够轻松解决很多问题,让我们共同体会几何模型的“数学之美”.

(1)【几何直观】如图1,![]() 中,
中,![]() ,
,![]() ,在
,在![]() 内部取一点
内部取一点![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 与
与![]() 的数量关系是__________;
的数量关系是__________;![]() 与
与![]() 的数量关系是__________;
的数量关系是__________;
(2)【类比推理】如图2,在正方形![]() 内部取一点
内部取一点![]() ,使
,使![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:四边形
,求证:四边形![]() 是正方形;
是正方形;
(3)【深度探究】如图3,矩形![]() 中,
中,![]() ,
,![]() ,在其内部取一点
,在其内部取一点![]() ,使
,使![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() __________;
__________;
(4)【拓展延伸】在矩形![]() 中,点
中,点![]() 为
为![]() 边上的一点,连接
边上的一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
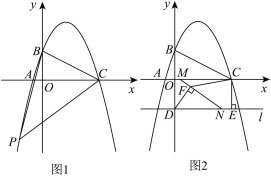
24.综合与探究
如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上的点,连接
下方抛物线上的点,连接![]() ,
,![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)点![]() 是第四象限内抛物线上的一点,连接
是第四象限内抛物线上的一点,连接![]() ,若
,若![]() ,则点
,则点![]() 的坐标为__________;
的坐标为__________;
(4)如图2,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,过点
,过点![]() 作
作![]() 轴的平行线l,过点
轴的平行线l,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,动点
,动点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,动点
同时出发,动点![]() 以每秒
以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向匀速运动,动点
方向匀速运动,动点![]() 以每秒
以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向匀速运动(当点
方向匀速运动(当点![]() 到达点
到达点![]() 时,点
时,点![]() ,
,![]() 都停止运动),连接
都停止运动),连接![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,连接
,连接![]() ,则
,则![]() 的取值范围是__________
的取值范围是__________
参考答案
1.B
2.D
3.A
4.C
5.A
6.C
7.D
8.B
9.A
10.B
11.![]()
12.![]() 且
且![]()
13.160
14.![]()
15.![]()
16.![]() 或
或![]()
17.![]()
18.(1)![]() ;(2)
;(2)![]()
19.![]() ,
,![]()
20.(1)24
(2)见解析
(3)![]()
(4)960人
【详解】(1)解:随机抽取部分学生的总人数为![]() (人),
(人),
∴![]() ,
,
即![]() ,
,
故答案为:![]()
(2)随机抽取部分学生中最喜爱篮球运动的学生数为:![]() (人),补全条形统计图如下:
(人),补全条形统计图如下:

(3)“足球”对应扇形的圆心角为![]() ,
,
故答案为:![]()
(4)![]() (人)
(人)
答:估计该校最喜爱篮球运动的学生有![]() 人.
人.
21.(1)见解析
(2)![]()
【详解】(1)证明:连接![]() ,
,
![]() 是
是![]() 的直径,
的直径,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,即
,即![]() ,
,
![]() .
.
![]() 为
为![]() 的半径,
的半径,
![]() 是
是![]() 的切线
的切线

22.
(1)![]()
(2)![]()
(3)7分或11分或13分
23.
(1)相等(或![]() );相等(或
);相等(或![]() )
)
(2)见解析
(3)![]()
(4)![]()
【详解】
(2)证明:∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]()
∵![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,
,
∴![]()
∵![]() ,
,
∴![]() 即
即![]()
∴![]()
∴![]() ,
,
∵![]()
∴![]()
∴![]()
∴四边形![]() 是矩形
是矩形
又∵![]()
∴四边形![]() 是正方形;
是正方形;
24.
(1)![]()
(2)![]() ,
,![]()
(3)![]()
(4)![]()
