2025年浙江中考数学试题及答案
选择题部分
一、选择题（本大题共10小题，每小题3分，共30分．每小题列出的四个选项中只有一个是符合题目要求的，不选、多选、错选均不得分）
1. 
的相反数是（ ）
A. 
B. 
C. 
D. 
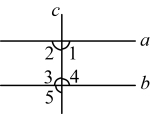
2. 如图所示，直线
被直线c所截．若
，则（ ）
A. 
B. 
C. 
D. 
3. 国家税务总局发布的数据显示，2024年，现行支持科技创新和制造业发展的主要政策减税降费及退税达26293亿元，助力我国新质生产力加速培育、制造业高质量发展．将数2629300000000用科学记数法表示为（ ）
A
B. 
C. 
D. 
4. 底面是正六边形的直棱柱如图所示，其俯视图是（ ）
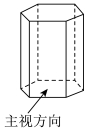
A.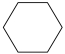 
B. 
C. 
D. 
5. 已知反比例函数
．下列选项正确的是（ ）
A. 函数图象在第一、三象限B. y随x的增大而减小
C. 函数图象在第二、四象限D. y随x
增大而增大
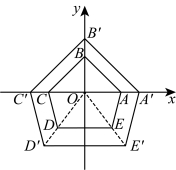
6. 如图，五边形
是以坐标原点O为位似中心的位似图形，已知点
的坐标分别为
．若
的长为3，则
的长为（ ）
A. 
B. 4C. 
D. 5
7. 手工社团的同学制作两种手工艺品A和B，需要用到彩色纸和细木条，单个手工艺品材料用量如下表．
材料 类别 | 彩色纸（张） | 细木条（捆） |
手工艺品A | 5 | 3 |
手工艺品B | 2 | 1 |
如果一共用了17张彩色纸和10捆细木条，问他们制作的两种手工艺品各有多少个？设手工艺品A有x个，手工艺品B有y个，则x和y满足的方程组是（ ）
A. 
B. 
C. 
D. 
8. 某书店某一天图书的销售情况如图所示．
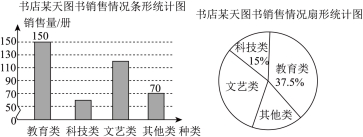
根据以上信息，下列选项错误的是（ ）
A. 科技类图书销售了60册B. 文艺类图书销售了120册
C. 文艺类图书销售占比
D. 其他类图书销售占比
9. 如图，在
中，
是斜边
上的中线，以点C为圆心，
长为半径作弧，与
的另一个交点为点E．若
，则
的长为（ ）
A. 
B. 
C. 
D. 
10. 为了实时规划路径，卫星导航系统需要计算运动点与观测点之间距离
平方．如图1，点P是一个固定观测点，运动点Q从A处出发，沿笔直公路
向目的地B处运动．设
为x（单位：
）
为y（单位：
）．如图2，y关于x的函数图象与y轴交于点C，最低点
，且经过
和
两点．下列选项正确的是（ ）
A. 
B. 
C. 点C的纵坐标为240D. 点
在该函数图象上
非选择题部分
二、填空题（本大题共6小题，每小题3分，共18分）
11. 
________．
12. 不等式组
的解集是________
13. 无人机警戒在高速公路场景中的应用，是我国低空经济高质量发展的重要实践方向．如图，在高速公路上，交警在A处操控无人机巡查，无人机从点A处飞行到点P处悬停，探测到它的正下方公路上点B处有汽车发生故障．测得A处到P处的距离为
，从点A观测点P的仰角为
，则A处到B处的距离为________
．
14. 现有六张分别标有数字
的卡片，其中标有数字
的卡片在甲手中，标有数字
的卡片在乙手中．两人各随机出一张卡片，甲出的卡片数字比乙大的概率是________．
15. 【文化欣赏】
我国南宋时期数学家杨辉于1261年写下《详解九章算法》，书中记载的二项和的乘方
展开式的系数规律如图所示，其中“三乘”对应的展开式：
．
【应用体验】
已知
，则m
值为________
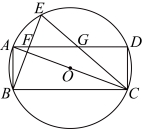
16. 如图，矩形
内接于
是
上一点，连接
分别交
于点
．若
，则
的直径为________
三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤）
17. 化简求值：
，其中
．
18. 解分式方程：
．
19. 【问题背景】
如图所示，某兴趣小组需要在正方形纸板
上剪下机翼状纸板（阴影部分），点E在对角线
上．
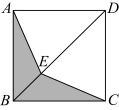
【数学理解】
（1）该机翼状纸板是由两个全等三角形组成，请写出
的证明过程．
（2）若裁剪过程中满足
，求“机翼角”
的度数．
20. 2024年11月9日是浙江省第31个消防日，为增强师生消防安全意识、提高自数防范能力，某县教育与消防部门共同组织消防知识竞赛．全县九年级共120个班，每班选派10名选手参加．随机抽取其中10个班级，统计其获奖人数，结果如下表．
班级 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
获奖人数 | 7 | 8 | 6 | 8 | 6 | 6 | 9 | 7 | 8 | 5 |
（1）若①班获奖选手的成绩分别为（单位：分）：
，求该班获奖选手成绩的众数与中位数．
（2）根据统计信息，估计全县九年级参赛选手获奖的总人数．
21. 【阅读理解】
同学们，我们来学习利用完全平方公式：
近似计算算术平方根的方法．
例如求
的近似值．
因为
，
所以
，
则
可以设成以下两种形式：
①
，其中
；
②
，其中
．
小明以①的形式求
的近似值的过程如图．
因 所以 即 因为 将 所以 即 得 故 |
，
，
．
比较小，
忽略不计，
，
，
，
．【尝试探究】
（1）请用②的形式求
的近似值（结果保留2位小数）．
【比较分析】
（2）你认为用哪一种形式得出的
的近似值的精确度更高，请说明理由．
22. 如图，在
中，
，点O在边
上，以点O为圆心，
长为半径的半圆，交
于点D，与
相切于点E，连接
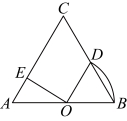
（1）求证：
．
（2）若
，求四边形
的面积．
23. 已知抛物线
（a为常数）经过点
．
（1）求a的值．
（2）过点
与x轴平行的直线交抛物线于
两点，且点B为线段
的中点，求t的值．
（3）设
，抛物线的一段
夹在两条均与x轴平行的直线
之间．若直线
之间的距离为16，求
的最大值．
24. 在菱形
中，
．
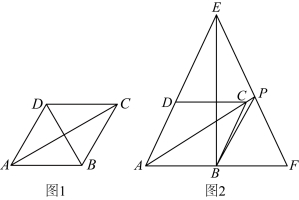
（1）如图1，求
的值．
（2）如图2，E是
延长线上的一点，连接
，作
与
关于直线
对称，
交射线
于点P，连接
．
①当
时，求
的长．
②求
的最小值
参考答案
选择题部分
一、选择题（本大题共10小题，每小题3分，共30分．每小题列出的四个选项中只有一个是符合题目要求的，不选、多选、错选均不得分）
【1题答案】
【答案】A
【2题答案】
【答案】B
【3题答案】
【答案】B
【4题答案】
【答案】A
【5题答案】
【答案】C
【6题答案】
【答案】C
【7题答案】
【答案】C
【8题答案】
【答案】D
【9题答案】
【答案】B
【10题答案】
【答案】D
非选择题部分
二、填空题（本大题共6小题，每小题3分，共18分）
【11题答案】
【答案】2
【12题答案】
【答案】
【13题答案】
【答案】
【14题答案】
【答案】
【15题答案】
【答案】
【16题答案】
【答案】
三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤）
【17题答案】
【答案】
，13
【18题答案】
【答案】
【19题答案】
【答案】（1）见解析 （2）
【20题答案】
【答案】（1）众数为
，中位数为
（2）全县九年级参赛选手获奖的总人数为
人．
【21题答案】
【答案】（1）
；（2）用①的形式得出的
的近似值的精确度更高，理由见解析
【22题答案】
【答案】（1）见解析 （2）
【23题答案】
【答案】（1）
（2）
（3）8
【24题答案】
【答案】（1）
（2）①
；②