2025年甘肃定西中考数学试题及答案
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1. -2+5=( )
A. -10B. -7C. -3D. 3
2. 根据国家统计局的数据,2024年中国生产芯片约451420000000颗,彰显了中国芯片产业的强大实力.数据451420000000用科学记数法可以表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 下列计算正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
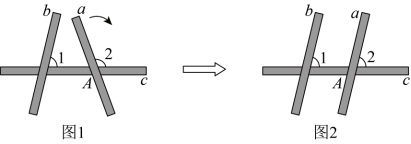
4. 如图1,三根木条a,b,c相交成![]() ,
,![]() ,固定木条b,c,将木条a绕点A顺时针转动至如图2所示,使木条a与木条b平行,则可将木条a旋转( )
,固定木条b,c,将木条a绕点A顺时针转动至如图2所示,使木条a与木条b平行,则可将木条a旋转( )
A
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 关于x的一元二次方程![]() 有两个实数根,则m的取值范围是( )
有两个实数根,则m的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 如图,一个多边形纸片的内角和为![]() ,按图示的剪法剪去一个内角后,所得新多边形的边数为( )
,按图示的剪法剪去一个内角后,所得新多边形的边数为( )
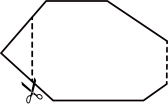
A. 12B. 11C. 10D. 9
7. 如图,四边形![]() 内接于
内接于![]() ,
,![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的度数为( )
的度数为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 习近平总书记致首届全民阅读大会举办的贺信指出:阅读是人类获取知识、启智增慧、培养道德的重要途径,可以让人得到思想启发,树立崇高理想,涵养浩然之气.中华民族自古提倡阅读,讲究格物致知、诚意正心,传承中华民族生生不息的精神,塑造中国人民自信自强的品格.如图是某网站连续多年对其用户书籍阅读量的统计图,下列结论错误的是( )

A. 2022年,人均纸质书籍阅读量为5本
B. 2023年,人均电子书籍阅读量为11本
C. 2024年,人均电子书籍阅读量是人均纸质书籍阅读量的3倍
D. 2016年至2024年,人均电子书籍阅读量逐年上升
9. 如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置![]() ,喷头M向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度
,喷头M向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度![]() 与水平距离
与水平距离![]() 之间的关系式是
之间的关系式是![]() ,则水流喷出的最大高度是( )
,则水流喷出的最大高度是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
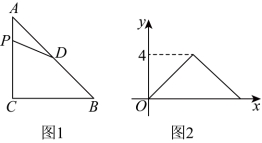
10. 如图1,在等腰直角三角形![]() 中,
中,![]() ,点D为边
,点D为边![]() 的中点.动点P从点A出发,沿边
的中点.动点P从点A出发,沿边![]() 方向匀速运动,运动到点B时停止.设点P的运动路程为x,
方向匀速运动,运动到点B时停止.设点P的运动路程为x,![]() 的面积为y,y与x的函数图象如图2所示,当点P运动到
的面积为y,y与x的函数图象如图2所示,当点P运动到![]() 的中点时,
的中点时,![]() 的长为( )
的长为( )
A. 2B. 2.5C. ![]() D. 4
D. 4
二、填空题:本大题共6小题,每小题4分,共24分.
11
因式分解:![]() ______.
______.
12. 方程![]() 的解是
的解是![]() _______.
_______.
13. 已知点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,如果
的图象上,如果![]() ,那么
,那么![]() _______(请写出一个符合条件的k值).
_______(请写出一个符合条件的k值).
14. 如图,把平行四边形纸片![]() 沿对角线
沿对角线![]() 折叠,点B落在点
折叠,点B落在点![]() 处,
处,![]() 与
与![]() 相交于点E,此时
相交于点E,此时![]() 恰为等边三角形.若
恰为等边三角形.若![]() ,则
,则![]() _______
_______![]() .
.
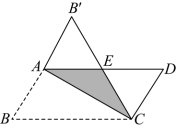
15. “儿童散学归来早,忙趁东风放纸鸢”.风筝古称纸鸢,起源于春秋战国时期,风筝制作技艺已被列入国家非物质文化遗产名录.为丰富校园生活,某校开展风筝制作活动,小言和哥哥制作了一大一小两个形状相同的风筝,风筝的形状如图所示,其中对角线![]() .已知大、小风筝的对应边之比为
.已知大、小风筝的对应边之比为![]() ,如果小风筝两条对角线的长分别为
,如果小风筝两条对角线的长分别为![]() 和
和![]() ,那么大风筝两条对角线长的和为________
,那么大风筝两条对角线长的和为________![]() .
.
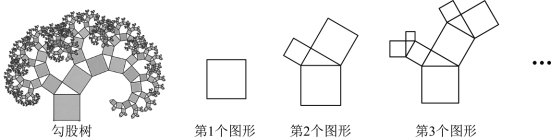
16. 勾股树是一个可以无限生长的树形图形,它既展示了数学中的精确与秩序,还蕴含了自然界的生长与繁衍之美.如图是勾股树及它的形成过程,其中第1个图形是正方形,第2个图形是以这个正方形的边长为斜边在其外部构造一个直角三角形,再以这个直角三角形的两条直角边为边长,分别向外生成两个新的正方形,重复上述步骤得到第3个图形,……,则第5个图形中共有_______个正方形.
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17. 计算:![]() .
.
18. 解不等式组: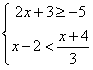
19. 化简:![]() .
.
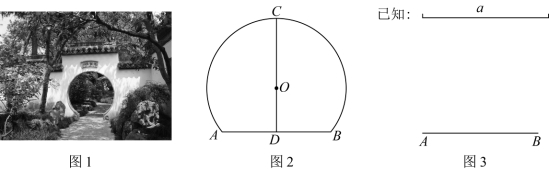
20. 如图1,月洞门是中国古典建筑中的一种圆形门洞,形如满月,故称“月洞门”,其形制可追溯至汉代,但真正在美学与功能上成熟于宋代,北宋建筑学家李诫编撰的《营造法式》是中国古代最完整的建筑技术典籍之一.如图2是古人根据《营造法式》中的“五举法”作出的月洞门的设计图,月洞门呈圆弧形,用![]() 表示,点O是
表示,点O是![]() 所在圆的圆心,
所在圆的圆心,![]() 是月洞门的横跨,
是月洞门的横跨,![]() 是月洞门的拱高.现在我们也可以用尺规作图的方法作出月洞门的设计图.如图3,已知月洞门的横跨为
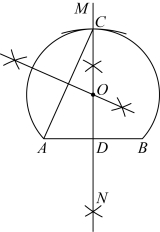
是月洞门的拱高.现在我们也可以用尺规作图的方法作出月洞门的设计图.如图3,已知月洞门的横跨为![]() ,拱高的长度为a.作法如下:
,拱高的长度为a.作法如下:
①作线段![]() 的垂直平分线
的垂直平分线![]() ,垂足为D;
,垂足为D;
②在射线![]() 上截取
上截取![]() ;
;
③连接![]() ,作线段
,作线段![]() 的垂直平分线交
的垂直平分线交![]() 于点O;
于点O;
④以点O为圆心,![]() 的长为半径作
的长为半径作![]() .
.
则![]() 就是所要作的圆弧.
就是所要作的圆弧.
请你依据以上步骤,用尺规作图的方法在图3中作出月洞门的设计图(保留作图痕迹,不写作法).
21. 如图是一个可以自由转动的转盘,转盘被等分成3个扇形,分别涂有“红、白、蓝”三种颜色,转盘指针固定.转动转盘、等转盘停止转动后,观察指针所落区域的颜色.若指针落在区域分界线上,则重新转动转盘.

(1)任意转动转盘一次,指针落在红色区域![]() 概率为_______;
概率为_______;
(2)任意转动转盘两次(第一次转动转盘,等转盘停止转动后,再第二次转动转盘),用画树状图或列表的方法求指针所落区域颜色不同的概率.
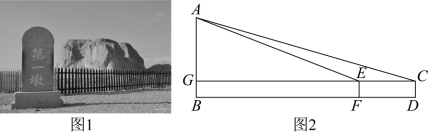
22. 如图1,位于嘉峪关的长城第一墩,又称天下第一墩,是明代万里长城最西端的一座墩台,始建于明嘉靖十八年(1539年).该墩台雄踞于讨赖河峡谷的悬崖之上,扼守丝绸之路咽喉要道,与嘉峪关关城、悬壁长城共同构成河西走廊的军事防御体系.随着岁月的变迁和自然的风化,长城第一墩的高度在慢慢降低.为了解长城第一墩的现存高度,某校同学们开展了“测量长城第一墩高度”的综合实践活动.如图2是他们测量长城第一墩高度AB的示意图,点A为最高点,点B,F,D是地面同一直线上的三个点(点D,F都在保护栅栏外),在D,F处分别用测角仪测得.![]() ,
,![]() ,其中
,其中![]() (测角仪的高度),
(测角仪的高度),![]() ,求长城第一墩的高度
,求长城第一墩的高度![]() (结果精确到0.1m).(参考数据:
(结果精确到0.1m).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23. 某校要从甲、乙两位射击队员中挑选一人参加比赛.在最近10次的选拔赛中,他们的射击成绩(单位:环)信息如下:
信息一:甲、乙队员的射击成绩
甲:10,8,8,10,6,8,6,9,10,8
乙:8,9,10,9,6,7,7,9,10, 8
信息二:甲、乙队员射击成绩的部分统计量
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8.3 | 8 | n | 2.01 |
乙 | 8.3 | m | 9 | 1.61 |
根据以上信息,回答下列问题:
(1)写出表中m,n的值:![]() _______,
_______,![]() _______;
_______;
(2)_______队员在射击选拔赛中发挥的更稳定(填“甲”或“乙”);
(3)小瑜认为甲、乙两人射击成绩的平均数一样,推荐哪位队员参赛都可以.你认为他说的对吗?请说明理由(写出一条合理的理由即可)
24. 如图,一次函数![]() 的图象交x轴于点A,交反比例函数
的图象交x轴于点A,交反比例函数![]() 的图象于点
的图象于点![]() .将一次函数
.将一次函数![]() 的图象向下平移
的图象向下平移![]() 个单位长度,所得的图象交x轴于点C.
个单位长度,所得的图象交x轴于点C.

(1)求反比例函数![]() 的表达式;
的表达式;
(2)当![]() 的面积为3时,求m的值.
的面积为3时,求m的值.
25. 如图,四边形![]() 的顶点A,B,C在
的顶点A,B,C在![]() 上,
上,![]() ,直径
,直径![]() 与弦
与弦![]() 相交于点F、点D是
相交于点F、点D是![]() 延长线上的一点且
延长线上的一点且![]() .
.
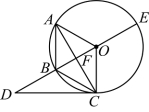
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若四边形![]() 是平行四边形,
是平行四边形,![]() .求
.求![]() 的长.
的长.
26. 四边形![]() 是正方形,点E是边
是正方形,点E是边![]() 上一动点(点D除外),
上一动点(点D除外),![]() 是直角三角形,
是直角三角形,![]() ,点G在
,点G在![]() 的延长线上.
的延长线上.
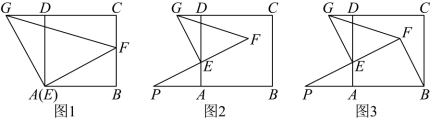
(1)如图1,当点E与点A重合,且点F在边![]() 上时,写出
上时,写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)如图2,当点E与点A不重合,且点F在正方形![]() 内部时,
内部时,![]() 的延长线与
的延长线与![]() 的延长线交于点P,如果
的延长线交于点P,如果![]() ,写出
,写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图3,在(2)的条件下,连接![]() ,写出
,写出![]() 和
和![]() 的数量关系,并说明理由
的数量关系,并说明理由
27. 如图1,抛物线![]() 分别与x轴,y轴交于A,
分别与x轴,y轴交于A,![]() 两点,M为
两点,M为![]() 的中点.
的中点.

(1)求抛物线的表达式;
(2)连接![]() ,过点M作
,过点M作![]()
![]() 垂线,交
垂线,交![]() 于点C,交抛物线于点D,连接
于点C,交抛物线于点D,连接![]() ,求
,求![]() 的面积;
的面积;
(3)点E为线段![]() 上一动点(点A除外),将线段
上一动点(点A除外),将线段![]() 绕点O顺时针旋转
绕点O顺时针旋转![]() 得到
得到![]() .
.
①当![]() 时,请在图2中画出线段
时,请在图2中画出线段![]() 后,求点F的坐标,并判断点F是否在抛物线上,说明理由;
后,求点F的坐标,并判断点F是否在抛物线上,说明理由;
②如图3,点P是第四象限![]() 一动点,
一动点,![]() ,连接
,连接![]() ,当点E运动时,求
,当点E运动时,求![]() 的最小值
的最小值
参考答案
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
【1题答案】
【答案】D
【2题答案】
【答案】C
【3题答案】
【答案】D
【4题答案】
【答案】A
【5题答案】
【答案】B
【6题答案】
【答案】A
【7题答案】
【答案】C
【8题答案】
【答案】C
【9题答案】
【答案】B
【10题答案】
【答案】A
二、填空题:本大题共6小题,每小题4分,共24分.
【11题答案】
【答案】![]() ##
##![]()
【详解】解:![]() ;
;
故答案为:![]() .
.
【12题答案】
【答案】![]()
【详解】解:![]() ,
,
去分母,得:![]() ,
,
解得:![]() ;
;
经检验![]() 是原方程的解,
是原方程的解,
故答案为:![]() .
.
【13题答案】
【答案】1(答案不唯一)
【详解】解:∵点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
又∵![]() ,
,![]() ,
,
∴在同一象限内![]() 随着
随着![]() 的增大而减小,
的增大而减小,
∴双曲线过一,三象限,
∴![]() ,
,
∴![]() (答案不唯一);
(答案不唯一);
故答案为:1(答案不唯一).
【14题答案】
【答案】12
【详解】解:∵折叠,
∴![]() ,
,
∵平行四边形纸片![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
故答案为:12
【15题答案】
【答案】195
【详解】解:![]() 小言和哥哥制作了一大一小两个形状相同的风筝,大、小风筝的对应边之比为
小言和哥哥制作了一大一小两个形状相同的风筝,大、小风筝的对应边之比为![]() ,
,
![]() 大风筝和小风筝相似,相似比为
大风筝和小风筝相似,相似比为![]() ,
,
![]() 大风筝两条对角线长:小风筝两条对角线长
大风筝两条对角线长:小风筝两条对角线长![]() ,
,
![]() 大风筝两条对角线的长分别为
大风筝两条对角线的长分别为![]() 和
和![]() ,
,
![]() 大风筝两条对角线长的和为
大风筝两条对角线长的和为![]() ,
,
故答案为:195.
【16题答案】
【答案】31
【详解】解:由图可知:第一个图形有1个正方形,
第2个图形有![]() 个正方形,
个正方形,
第3个图形有![]() 个正方形,
个正方形,
![]()
∴第5个图形中共有![]() 个正方形,
个正方形,
故答案为:31.
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
【17题答案】
【答案】![]()
【详解】解:原式![]()
![]() .
.
【18题答案】
【答案】![]()
【详解】解: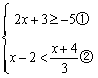 ,
,
解不等式①,得:![]() ,
,
解不等式②,得![]() ,
,
![]() 不等式组的解集为
不等式组的解集为![]() .
.
【19题答案】
【答案】![]()
【详解】解:原式![]()
![]()
![]()
![]() .
.
【20题答案】
【答案】图见解析
【详解】解:由题意,作图如下,![]() 即为所求;
即为所求;
【21题答案】
【答案】(1)![]()
(2)![]()
【详解】(1)解:由图可知,任意转动转盘一次,指针落在红色区域的概率为![]() ;
;
故答案为:![]() ;
;
(2)列表:
第二次 第一次 | 红 | 白 | 蓝 |
红 | (红,红) | (红,白) | (红,蓝) |
白 | (白,红) | (白,白) | (白,蓝) |
蓝 | (蓝,红) | (蓝,白) | (蓝,蓝) |
![]() 共有9种等可能结果,颜色不同的结果有6种,
共有9种等可能结果,颜色不同的结果有6种,
![]() .
.
【22题答案】
【答案】长城第一墩的高度![]() 为
为![]()
【详解】解:由题意,得:![]() ,
,![]() ,
,
设![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
答:长城第一墩的高度![]() 为
为![]() .
.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
【23题答案】
【答案】(1)![]()
(2)乙 (3)不对,理由见解析(答案不唯一,合理即可)
【详解】(1)解:乙中数据排序后,第5个和第6个数据分别为:![]() 和
和![]() ,
,
∴![]() ;
;
甲中数据出现次数最多的是![]() ,故
,故![]() ;
;
故答案为:![]() ;
;
(2)由表格可知:甲的方差大于乙的方差,
∴乙队员在射击选拔赛中发挥的更稳定;
故答案为:乙;
(3)小瑜说的不对,理由如下:
两人成绩的平均数相同,但是甲的方差大于乙的方差,故乙队员发挥更稳定,故应选乙队员参赛.
【24题答案】
【答案】(1)![]()
(2)![]()
【详解】(1)解:由题意得:点![]() 在一次函数
在一次函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]() ;
;
∵![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴反比例函数的表达式为![]() ;
;
(2)解:对于一次函数![]() ,令
,令![]() ,则
,则![]() ;
;
∴![]() ;
;
一次函数![]() 的图象向下平移
的图象向下平移![]() 个单位长度后的解析式为:
个单位长度后的解析式为:![]() ;
;
对于一次函数<img height="19" src="//img.985ks.com/images_new/img_default_show.png" data-src="//img.985ks.com/uploadfile/images/2025/0626/175094821628242gn: lef width="77"/>,令![]() ,则
,则![]() ;
;
∴![]() ;
;
∴![]() ;
;
解得:![]()
【25题答案】
【答案】(1)见解析 (2)![]()
【详解】(1)证明:如图1,连接![]() ,
,
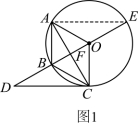
![]() ,
,![]() ,
,
![]() .
.
![]()
![]() ,
,
![]() .
.
![]()
![]() 是
是![]() 的直径,
的直径,
![]() ,即
,即![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
![]()
![]() 为
为![]() 的半径,
的半径,
![]()
![]() 是
是![]() 的切线.
的切线.
(2)解:如图2,

![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() .
.
又![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 是菱形,
是菱形,
![]() .
.
![]() 为等边三角形,
为等边三角形,
∴![]() .
.
![]() 在
在![]() 中,
中,![]() .
.
【26题答案】
【答案】(1)![]() ,理由见解析
,理由见解析
(2)![]() ,理由见解析
,理由见解析
(3)![]() ,理由见解析
,理由见解析
【详解】(1)解:![]() ,理由如下:
,理由如下:
∵正方形![]() ,
,
∴![]() ,
,
∵![]() 是直角三角形,
是直角三角形,![]() ,
,
∴![]() ,
,
当点E与点A重合时,则:![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵正方形![]() ,
,
∴![]() ,
,
∵点G在![]() 的延长线上,
的延长线上,![]() 的延长线与
的延长线与![]() 的延长线交于点P,
的延长线交于点P,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
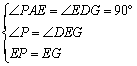 ,
,
∴![]() ,
,
∴![]() ;
;
(3)![]() ,理由如下:
,理由如下:
由(2)可知:![]() ,
,
∴![]() ,
,![]() ,
,
作![]() 于点
于点![]() ,则:
,则:![]() ,
,

∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为
为![]() 的中位线,
的中位线,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
在![]() 中,由勾股定理,得:
中,由勾股定理,得:![]() ,
,
∵![]() ,
,
∴![]() .
.
【27题答案】
【答案】(1)![]()
(2)![]()
(3)①![]() ,在抛物线上②
,在抛物线上②![]()
【详解】(1)解:把![]() ,代入
,代入![]() ,得:
,得:
![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(2)当![]() 时,则:
时,则:![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴设直线![]() 的解析式为:
的解析式为:![]() ,把
,把![]() ,代入,得:
,代入,得:![]() ,
,
∴![]() ,
,
∵点M作![]() 的垂线,交
的垂线,交![]() 于点C,交抛物线于点D,
于点C,交抛物线于点D,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 的面积
的面积![]() ;
;
(3)①由题意,作图如下:
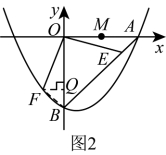
连接![]() ,作
,作![]() 于点
于点![]() ,
,
由(2)可知:![]() ,
,
∴![]() ,
,
∵旋转,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
对于![]() ,当
,当![]() 时,
时,![]() ,
,
∴点![]() 在抛物线上;
在抛物线上;
②连接![]() 并延长,交
并延长,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,如图,
,如图,

∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴当![]() 三点共线时,
三点共线时,![]() 最小,
最小,
同①可得,![]() ,
,
∴点![]() 在射线
在射线![]() 上运动,
上运动,
∴当![]() 时,即
时,即![]() 与点
与点![]() 重合时,
重合时,![]() 最小,此时
最小,此时![]() 最小为
最小为![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.
