2025年山东德州中考数学试题及答案
一、选择题:本题共10小题,每小题3分,共30分.每小题只有一个选项符合题目要求.
1.如图,数轴上表示-2的点是( )
![]()
A.MB.NC.PD.Q
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.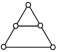 B.
B.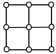 C.
C.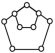 D.
D.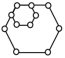
3.我国“深蓝2号”大型智能深海养殖网箱的主体是一个正六棱柱,其示意图的主视图是( )


A. B.
B. C.
C. D.
D.
4.好客山东以其宽厚仁德的人文情怀、风景秀丽的河海山川吸引了来自世界各地的朋友,据统计,山东省2024年全年接待游客超9亿人次.数据“9亿”用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知![]() ,则下列运算正确的是( )
,则下列运算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.某班学生到山东省博物馆参加研学活动.博物馆为同学们准备了以镇馆之宝“亚醜钺”“蛋壳黑陶杯”“颂簋”为主题的三款文创产品,每位同学可从中随机抽取一个作为纪念品.若抽到每一款的可能性相等,则甲、乙两位同学同时抽到“亚醜钺”的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.明代数学家吴敬的《九章算法比类大全》中有一个“哪吒夜叉”问题,大意是:有3个头6只手的哪吒若干,有1个头8只手的夜叉若干,两方交战,共有36个头,108只手.问哪吒、夜叉各有多少?设哪吒有![]() 个,夜叉有
个,夜叉有![]() 个,则根据条件所列方程组为( )
个,则根据条件所列方程组为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.在中国古代文化中,玉璧寓意宇宙的广阔与秩序,也经常被视为君子修身齐家的象征.下图是某玉璧的平面示意图,由一个正方形的内切圆和外接圆组成.已知内切圆的半径是2,则图中阴影部分的面积是( )
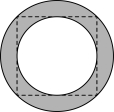
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图,在平面直角坐标系中,A,C两点在坐标轴上,四边形![]() 是面积为4的正方形.若函数
是面积为4的正方形.若函数![]() 的图象经过点
的图象经过点![]() ,则满足
,则满足![]() 的
的![]() 的取值范围为( )
的取值范围为( )
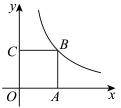
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在水分、养料等条件一定的情况下,某植物的生长速度![]() (厘米/天)和光照强度
(厘米/天)和光照强度![]() (勒克斯)之间存在一定关系.在低光照强度范围(
(勒克斯)之间存在一定关系.在低光照强度范围(![]() )内,
)内,![]() 与
与![]() 近似成一次函数关系;在中高光照强度范围
近似成一次函数关系;在中高光照强度范围![]() 内,
内,![]() 与
与![]() 近似成二次函数关系.其部分图象如图所示.根据图象,下列结论正确的是( )
近似成二次函数关系.其部分图象如图所示.根据图象,下列结论正确的是( )
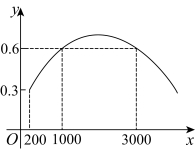
A.当![]() 时,
时,![]() 随
随![]() 的增大而减小B.当
的增大而减小B.当![]() 时,
时,![]() 有最大值
有最大值
C.当![]() 时,
时,![]() D.当
D.当![]() 时,
时,![]()
二、填空题:本题共5小题,每小题3分,共15分.
11.写出使分式![]() 有意义的
有意义的![]() 的一个值 .
的一个值 .
12.在平面直角坐标系中,将点![]() 向下平移2个单位长度,得到的对应点
向下平移2个单位长度,得到的对应点![]() 的坐标是 .
的坐标是 .
13.若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,则实数
有两个不相等的实数根,则实数![]() 的取值范围是 .
的取值范围是 .
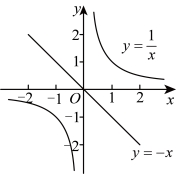
14.取直线![]() 上一点
上一点![]() ,①过点
,①过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ;②过点
;②过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ;如此循环进行下去.按照上面的操作,若点
;如此循环进行下去.按照上面的操作,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标是 .
的坐标是 .
15.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 为边
为边![]() 上异于
上异于![]() 的一点,以
的一点,以![]() ,
,![]() 为邻边作
为邻边作![]() ,则线段
,则线段![]() 的最小值是
的最小值是
三、解答题:本题共8小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.(1)计算:![]() ;
;
(2)先化简,再求值:![]() ,其中
,其中![]() .
.
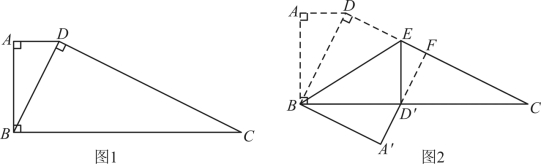
17.在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .如图1.
.如图1.

(1)求![]() 的度数;
的度数;
(2)已知![]() ,分别以
,分别以![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ,作直线
,作直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的延长线于点F.如图2,求
的延长线于点F.如图2,求![]() 的长.
的长.
18.山东省在能源绿色低碳转型过程中,探索出一条“以储调绿”的能源转型路径.某地结合实际情况,建立了一座圆柱形蓄水池,通过蓄水发电实现低峰蓄能、高峰释能,助力能源转型.
已知本次注水前蓄水池的水位高度为5米,注水时水位高度每小时上升6米.
(1)请写出本次注水过程中,蓄水池的水位高度y(米)与注水时间x(小时)之间的关系式;
(2)已知蓄水池的底面积为![]() 万平方米,每立方米的水可供发电
万平方米,每立方米的水可供发电![]() 千瓦时,求注水多长时间可供发电
千瓦时,求注水多长时间可供发电![]() 万千瓦时?
万千瓦时?
19.在2025年全国科技活动周期间,某校科技小组对甲、乙两个水产养殖基地水体的![]() 值进行了检测,并对一天(24小时)内每小时的
值进行了检测,并对一天(24小时)内每小时的![]() 值进行了整理、描述及分析.
值进行了整理、描述及分析.
【收集数据】
甲基地水体的![]() 值数据:
值数据:
7.27,7.28,7.34,7.35,7.36,7.51,7.53,7.67,7.67,7.67,7.67,7.81,7.81,7.88,7.91,8.01,8.02,8.03,8.07,8.16,8.17,8.23,8.26,8.26.
乙基地水体的![]() 值数据:
值数据:
7.11,7.12,7.14,7.25,7.36,7.52,7.63,7.67,7.69,7.75,7.77,7.77,7.81,7.84,7.89,8.01,8.12,8.13,8.14,8.16,8.17,8.18,8.20,8.21.
【整理数据】
| | | | | |
甲 | 2 | 5 | 7 | 7 | 3 |
乙 | 4 | 2 | 9 | a | 2 |
【描述数据】

【分析数据】
平均数 | 众数 | 中位数 | 方差 | |
甲 | 7.79 | b | 7.81 | 0.10 |
乙 | 7.78 | 7.77 | c | 0.13 |
根据以上信息解决下列问题:
(1)补全频数分布直方图;
(2)填空:![]() ______,
______,![]() ______;
______;
(3)请判断甲、乙哪个基地水体的![]() 值更稳定,并说明理由;
值更稳定,并说明理由;
(4)已知两基地对水体![]() 值的日变化量(
值的日变化量(![]() 值最大值与最小值的差)要求为0.5~1,分别判断并说明该日两基地的
值最大值与最小值的差)要求为0.5~1,分别判断并说明该日两基地的![]() 值是否符合要求.
值是否符合要求.
20.如图,在![]() 中,点
中,点![]() 在
在![]() 上,边
上,边![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.![]() 是
是![]() 的平分线.
的平分线.

(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() 的半径为2,
的半径为2,![]() ,求
,求![]() 的长.
的长.
21.【问题情境】
2025年5月29日“天问二号”成功发射,开启了小行星伴飞取样探测的新篇章.某校航天兴趣小组受到鼓舞,制作了一个航天器模型,其中某个部件使用3D打印完成,如图1.
【问题提出】
部件主视图如图2所示,由于1的尺寸不易直接测量,需要设计一个可以得到![]() 的长度的方案,以检测该部件中
的长度的方案,以检测该部件中![]() 的长度是否符合要求.
的长度是否符合要求.

【方案设计】
兴趣小组通过查阅文献,提出了钢柱测量法.
测量工具:游标卡尺、若干个底面圆半径相同的钢柱(圆柱).
操作步骤:如图3,将两个钢柱平行放在部件合适位置,使得钢柱与部件紧密贴合.示意图如图4,![]() 分别与
分别与![]() ,
,![]() 相切于点
相切于点![]() ,
,![]() .用游标卡尺测量出
.用游标卡尺测量出![]() 的长度
的长度![]() .
.

【问题解决】
已知![]() ,
,![]() 的长度要求是
的长度要求是![]() .
.
(1)求![]() 的度数;
的度数;
(2)已知钢柱的底面圆半径为![]() ,现测得
,现测得![]() .根据以上信息,通过计算说明该部件
.根据以上信息,通过计算说明该部件![]() 的长度是否符合要求.(参考数据:
的长度是否符合要求.(参考数据:![]() )
)
【结果反思】
(3)本次实践过程借助圆柱将不可测量的长度转化为可测量的长度,能将圆柱换成其他几何体吗?如果能,写出一个;如果不能,说明理由.
22.已知二次函数![]() ,其中
,其中![]() ,
,![]() 为两个不相等的实数.
为两个不相等的实数.
(1)当![]() 、
、![]() 时,求此函数图象的对称轴;
时,求此函数图象的对称轴;
(2)当![]() 时,若该函数在
时,若该函数在![]() 时,y随
时,y随![]() 的增大而减小;在
的增大而减小;在![]() 时,
时,![]() 随
随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
(3)若点![]() ,
,![]() ,
,![]() 均在该函数的图象上,是否存在常数
均在该函数的图象上,是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
23.【图形感知】
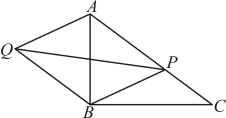
如图1,在四边形![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
【探究发现】
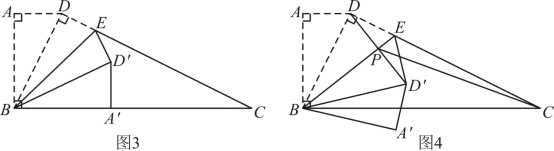
老师指导同学们对图1所示的纸片进行了折叠探究.
在线段![]() 上取一点
上取一点![]() ,连接
,连接![]() .将四边形
.将四边形![]() 沿
沿![]() 翻折得到四边形
翻折得到四边形![]() ,其中
,其中![]() ,
,![]() 分别是A,D的对应点.
分别是A,D的对应点.
(2)其中甲、乙两位同学的折叠情况如下:
①甲:点![]() 恰好落在边
恰好落在边![]() 上,延长
上,延长![]() 交
交![]() 于点
于点![]() ,如图2.判断四边形
,如图2.判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
②乙:点![]() 恰好落在边
恰好落在边![]() 上,如图3.求
上,如图3.求![]() 的长;
的长;
(3)如图4,连接![]() 交
交![]() 于点P,连接
于点P,连接![]() .当点E在线段
.当点E在线段![]() 上运动时,线段
上运动时,线段![]() 是否存在最小值?若存在,直接写出;若不存在,说明理由.
是否存在最小值?若存在,直接写出;若不存在,说明理由.
参考答案
1.A
2.B
3.C
4.C
5.B
6.A
7.D
8.D
9.A
10.B
11.1(不唯一)
12.![]()
13.![]()
14.![]()
15.![]()
16.(1)2;(2)![]() ,4
,4
17.(1)![]() ;
;
(2)![]() .
.
18.(1)![]()
(2)注水5小时可供发电![]() 万千瓦时.
万千瓦时.
19.
(1)见解析
(2)![]() ;
;![]()
(3)甲基地水体的![]() 值更稳定,理由见详解;
值更稳定,理由见详解;
(4)甲符合要求,乙不符合要求.
【详解】(1)解:根据题意得![]() ,
,
补全频数分布直方图如图;
 ;
;
(3)解:∵甲的方差为0.10,乙的方差为0.13,![]() ,
,
∴甲基地水体的![]() 值更稳定;
值更稳定;
20.
(1)见解析
(2)![]() .
.
【详解】(1)证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的平分线,
的平分线,
∴![]() ,
,
∴![]() ,
,
即![]() 且
且![]() 为半径,
为半径,
∴![]() 为
为![]() 的切线;
的切线;
21.(1)![]() ;(2)该部件
;(2)该部件![]() 的长度符合要求;(3)见解析
的长度符合要求;(3)见解析
【详解】
(3)能,将圆柱换成正方体.如图,

设正方体的棱长为![]() ,用游标卡尺测量出
,用游标卡尺测量出![]() 的长度
的长度![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ .
.
22.(1)![]()
(2)![]()
(3)![]()
23.(1)![]() ;(2)①四边形
;(2)①四边形![]() 是矩形,理由见解析;②
是矩形,理由见解析;②![]() ;(3)线段
;(3)线段![]() 的最小值为
的最小值为![]()
