2025年福建中考数学试题及答案

2025年福建中考数学试题及答案

　　一、选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合要求的．

　　1．下列实数中，最小的数是（    ）

　　A．-1B．0C．D．2

　　2．中国古算诗词歌赋较多．古算诗词题，是反映数学数量关系的内在联系及其规律的一种文学浪漫形式．下列分别是古算诗词题“圆中方形”“方形圆径”“圆材藏壁”“勾股容圆”所描绘的图形，其中既不是轴对称图形也不是中心对称图形的是（    ）

　　A．B．C．D．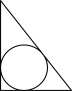

　　3．若在实数范围内有意义，则实数x的值可以是（    ）

　　A．B．C．0D．2

　　4．福建博物院收藏着一件“镇馆之宝”——云纹青铜大绕，如图1．云纹青铜大绕是西周乐器，鼓饰变形兽面纹，两侧饰云雷纹，浑大厚重，作风稳重古朴，代表了福建古代青铜文化曾经的历史和辉煌．图2为其示意图，它的主视图是（    ）

　　A．B．C．D．

　　5．不等式的解集在数轴上表示正确的是（    ）

　　A．B．

　　C．D．

　　6．在分别写有，1，2的三张卡片中，不放回地随机抽取两张，这两张卡片上的数恰好互为相反数的概率是（    ）

　　A．B．C．D．

　　7．某数学兴趣小组为探究平行线的有关性质，用一副三角尺按如图所示的方式摆放，其中点A，E，C，F在同一条直线上，．当时，的大小为（    ）

　　A．B．C．D．

　　8．为加强劳动教育，增加学生实践机会，某校拟用总长为5米的篱笆，在两边都足够长的直角围墙的一角，围出一块6平方米的矩形菜地作为实践基地，如图所示．设矩形的一边长为x米，根据题意可列方程（    ）

　　A．B．C．D．

　　9．如图，与相切于点A，的延长线交于点C．，且交于点B．若，则的大小为（    ）

　　A．B．C．D．

　　10．已知点在抛物线上，若，则下列判断正确的是（    ）

　　A．B．C．D．

　　二、填空题：本题共6小题，每小题4分，共24分．

　　11．为响应“体重管理年”有关倡议，小敏对自己的体重进行了跟踪统计．为方便记录，他将体重增加记作，那么体重减少应记作       ．

　　12．某房梁如图所示，立柱，E，F分别是斜梁，的中点．若，则的长为       m．

　　13．若反比例函数的图象过点，则常数       ．

　　14．如图，菱形的对角线相交于点O，过点O且与边分别相交于点E，F．若，则与的面积之和为       ．

　　15．某公司为选拔英语翻译员，举行听、说、读、写综合测试，其中听、说、读、写各项成绩（百分制）按的比例计算最终成绩．参与选拔的甲、乙两位员工的听、说、读、写各项测试成绩及最终成绩如下表：

　　由以上信息，可以判断A，B的大小关系是A       B．（填“>”“=”或“<”）

　　16．弹簧秤是根据胡克定律并利用物体的重力来测量物体质量的．胡克定律为：在弹性限度内，弹簧弹力F的大小与弹簧伸长（或压缩）的长度x成正比，即，其中k为常数，是弹簧的劲度系数；质量为m的物体重力为，其中g为常数．如图，一把弹簧秤在不挂任何物体时弹簧的长度为6厘米．在其弹性限度内：当所挂物体的质量为0.5千克时，弹簧长度为6.5厘米，那么，当弹簧长度为6.8厘米时，所挂物体的质量为       千克．

　　三、解答题：本题共9小题，共86分．解答应写出文字说明、证明过程或演算步骤．

　　17．计算：

　　18．如图，点E，F分别在的延长线上，．求证：．

　　19．先化简，再求值：，其中．

　　20．甲、乙两人是新华高级中学数学兴趣小组成员．以下是他们在参加高中数学联赛预备队员集训期间的测试成绩及当地近五年高中数学联赛的相关信息．

　　信息一：甲、乙两人集训期间的测试成绩（单位：分）

　　其中，甲、乙成绩的平均数分别是；方差分别是．

　　信息二：当地近五年高中数学联赛获奖分数线（单位：分）

　　试根据以上信息及你所学的统计学知识，解决以下问题：

　　(1)计算a的值，并根据平均数与方差对甲、乙的成绩进行评价；

　　(2)计算当地近五年高中数学联赛获奖分数线的平均数，并说明：若要从中选择一人参加高中数学联赛，选谁更合适；

　　(3)若要从中选择一人参加进一步的培养，从发展潜能的角度考虑，你认为选谁更合适？为什么？

　　21．如图，是等边三角形，D是的中点，，垂足为C，是由沿方向平移得到的．已知过点A，交于点G．

　　(1)求的大小；

　　(2)求证：是等边三角形．

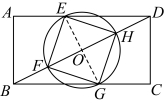
　　22．如图，矩形中，．

　　(1)求作正方形，使得点E，G分别落在边上，点F，H落在上；（要求：尺规作图，不写作法，保留作图痕迹）

　　(2)若，求（1）中所作的正方形的边长．

　　23．在平面直角坐标系中，二次函数的图象过点．

　　(1)求的值；

　　(2)已知二次函数的最大值为．

　　①求该二次函数的表达式；

　　②若为该二次函数图象上的不同两点，且，求证：．

　　24．阅读材料，回答问题．

　　(1)解决问题1；

　　(2)请把①②所缺的证明过程补充完整；

　　(3)解决问题2．

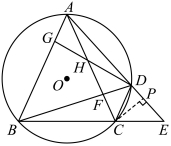
　　25．如图，四边形ABCD内接于，AD，BC的延长线相交于点E，AC，BD相交于点F．G是AB上一点，GD交AC于点H，且．

　　(1)求证：；

　　(2)求证：；

　　(3)若，求的周长

参考答案

　　1．A

　　2．D

　　3．D

　　4．A

　　5．C

　　6．B

　　7．B

　　8．C

　　9．C

　　10．A

　　11．

　　12．4

　　13．

　　14．1

　　15．>

　　16．0.8

　　17．

　　18．

　　【详解】证明：，

　　．

　　在和中，

　　，

　　，

　　．

　　19．，

　　20．

　　(1)，见解析

　　(2)甲，见解析

　　(3)选甲更合适．理由见解析

　　【详解】

　　（1），即．

　　因为，

　　所以，

　　所以甲、乙两人的整体水平相当，但乙的成绩比甲稳定．

　　（2）由已知得，获奖分数线的平均数为，

　　从信息一可知，在集训期间的十次测试成绩中，甲达到获奖分数线的平均数的频数为4，而乙的频数为1，所以甲获奖的可能性更大，故选甲参加更合适．

　　（3）选甲更合适．理由：在集训期间的十次测试成绩中，甲呈上升趋势，而乙基本稳定在原有的水平，故从发展潜能的角度考虑，选甲更合适．

　　21．

　　(1)

　　(2)见解析

　　【详解】

　　（1）解：是等边三角形，

　　．

　　D是的中点，

　　．

　　，

　　，

　　．

　　（2）由平移可知：，

　　，

　　又，

　　，

　　∴，

　　又，

　　垂直平分，

　　，

　　由（1）知，，

　　，

　　，

　　是等边三角形．

　　22．

　　(1)见解析

　　(2)

　　【详解】（1）解：如图，四边形就是所求作的正方形．

　　由作图可知，，，

　　∵矩形，

　　∴，

　　∴，，

　　∴，

　　∴，

　　由作图可知，，

　　∴四边形为矩形，

　　∵，

　　∴四边形为正方形；

　　（2）由（1）知：，，

　　四边形是矩形，

　　，

　　在中，，

　　，

　　．

　　，

　　．

　　又，

　　，

　　，即，

　　．

　　在中，，

　　，

　　∴正方形EFGH的边长为．

　　23．

　　(1)

　　(2)①；②见解析

　　【详解】

　　②因为点在函数的图象上，

　　所以．

　　由①知，点关于直线对称，不妨设，

　　则，即．

　　所以

　　，

　　所以．

　　24．

　　(1)小明的猜想不正确，反例：

　　(2)见解析

　　(3)当A的数字大于或等于B的数字时，的位数是；当A的数字小于B的数字时，的位数是

　　【详解】

　　（2）证明：①，所以，所以，与（*）矛盾，不合题意；

　　②，所以，又，所以，

　　由（*）知，所以．

　　25．

　　(1)见解析

　　(2)见解析

　　(3)

　　【详解】（1）证明：，

　　．

　　，

　　，

　　．

　　，

　　．

　　（2）证明：，

　　．

　　，

　　，

　　又，

　　，

　　，

　　．

　　由（1）知，，

　　又，

　　，

　　．

　　，

　　．

　　∵，

　　，

　　，

　　，

　　．

　　（3）解：由（2）知，，

　　的周长为．

　　设，则．

　　由（2）可知，．

　　又，

　　，

　　，

　　，

　　．

　　又，

　　，

　　．

　　过点C作，垂足为P，则．

　　四边形是圆内接四边形，

　　，

　　又，

　　，

　　．

　　在中，，即．

　　，

　　，

　　，

　　．

　　在中，，

　　，

　　解得，或（舍去）．

　　．

　　的周长为．