2025年四川泸州中考数学试题及答案
全卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页.全卷满分120分.考试时间共120分钟.
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列各组数中,互为相反数的是( )
A.![]() 和
和![]() B.
B.![]() 和
和![]() C.2和
C.2和![]() D.
D.![]() 和
和![]()
2.据我国文化和旅游部数据中心测算,2025年“五一”期间,国内游客出游![]() 人次,将数据
人次,将数据![]() 用科学记数法表示为( )
用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
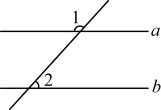
3.如图,直线![]() ,若
,若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列人工智能助手图标中,是轴对称图形的是( )
A.![]() B.
B. C.
C. D.
D.
5.下列运算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.某校七年级甲、乙、丙、丁四名同学参加1分钟跳绳测试,每人10次跳绳成绩的平均数(单位:个)及方差(单位:个2)如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 205 | 217 | 208 | 217 |
方差 | 4.6 | 4.6 | 6.9 | 9.6 |
根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加比赛,应选择( )
A.甲B.乙C.丙D.丁
7.矩形具有而菱形不具有的性质是( )
A.对角线相等B.对角线互相平分C.对角线互相垂直D.对角相等
8.如图,四边形![]() 内接于
内接于![]() ,
,![]() 为
为![]() 的直径.若
的直径.若![]() ,则
,则![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.《九章算术》是中国古代一部重要的数学著作,在“方程”章中记载了求不定方程(组)解的问题.例如方程![]() 恰有一个正整数解
恰有一个正整数解![]() .类似地,方程
.类似地,方程![]() 的正整数解的个数是( )
的正整数解的个数是( )
A.1B.2C.3D.4
10.已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的交点位于
轴的交点位于![]() 轴下方,且
轴下方,且![]() 时,
时,![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.如图,在边长为2的正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上的点,且
上的点,且![]() ,则
,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.对于任意实数![]() ,定义新运算:
,定义新运算:![]()
![]()
![]() ,给出下列结论:①
,给出下列结论:①![]()
![]() ;②若
;②若![]()
![]()
![]() ,则
,则![]() ;③
;③![]()
![]()
![]()
![]()
![]() ;④若
;④若![]()
![]()
![]() ,则
,则![]() 的取值范围为
的取值范围为![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.1B.2C.3D.4
第Ⅱ卷(非选择题 共84分)
注意事项:用0.5毫米黑色墨迹签字笔在答题卡上对应题号位置作答,在试卷上作答无效.
二、填空题(本大题共4个小题,每小题3分,共12分)
13.若点![]() 在第一象限,则
在第一象限,则![]() 的取值范围是 .
的取值范围是 .
14.一组数据3,2,6,7,4,6的中位数是 .
15.若一元二次方程![]() 的两根为
的两根为![]() ,则
,则![]() 的值为 .
的值为 .
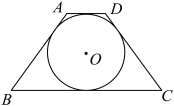
16.如图,梯形![]() 中,
中,![]() ,
,![]() 与梯形
与梯形![]() 的各边都相切,且
的各边都相切,且![]() 的面积为
的面积为![]() ,则点
,则点![]() 到
到![]() 的距离为 .
的距离为 .
三、本大题共3个小题,每小题6分,共18分.
17.计算:![]() .
.
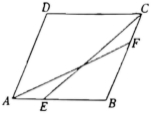
18.如图,在菱形![]() 中,
中,![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() .
.
求证:![]() .
.
19.化简:![]() .
.
四、本大题共2个小题,每小题7分,共14分.
20.某市教育综合实践基地开设有![]() :巧手木艺;
:巧手木艺;![]() :创意缝纫;
:创意缝纫;![]() :快乐种植;
:快乐种植;![]() :美味烹饪;
:美味烹饪;![]() :爱心医护等五门课程.某校组织八年级学生到该基地开展活动,一段时间后,基地采用随机抽样的方式,在该校八年级抽取部分学生开展了“我最喜欢的综合实践课程”的问卷调查,并根据调查所收集的数据进行整理,绘制了如下两幅不完整的统计图表.
:爱心医护等五门课程.某校组织八年级学生到该基地开展活动,一段时间后,基地采用随机抽样的方式,在该校八年级抽取部分学生开展了“我最喜欢的综合实践课程”的问卷调查,并根据调查所收集的数据进行整理,绘制了如下两幅不完整的统计图表.
课程名称 | 巧手木艺 | 创意缝纫 | 快乐种植 | 美味烹饪 | 爱心医护 |
人数 | | 6 | 12 | | 18 |
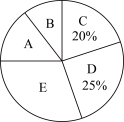
根据图表信息,回答下列问题:
(1)![]() ______,扇形统计图中表示“巧手木艺”部分对应扇形的圆心角度数是________;
______,扇形统计图中表示“巧手木艺”部分对应扇形的圆心角度数是________;
(2)若该校八年级共有480名学生,请你估计该校八年级最喜欢![]() 两门课程的学生人数;
两门课程的学生人数;
(3)小明同学从![]() 四门课程中随机选择两门,求恰好选中
四门课程中随机选择两门,求恰好选中![]() 两门课程的概率.
两门课程的概率.
21.某超市购进甲、乙两种商品,2022年甲、乙两种商品每件的进价均为125元,随着生产成本的降低,甲种商品每件的进价年平均下降25元,乙种商品2024年每件的进价为80元.
(1)求乙种商品每件进价的年平均下降率;
(2)2024年该超市用不超过7800元的资金一次购进甲、乙两种商品共100件,求最少购进多少件甲种商品.
五、本大题共2个小题,每小题8分,共16分.
22.如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的一个交点为
的图象的一个交点为![]() .
.
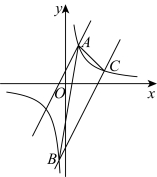
(1)求一次函数与反比例函数的解析式;
(2)将一次函数![]() 的图象沿
的图象沿![]() 轴向下平移12个单位,与反比例函数
轴向下平移12个单位,与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,求
,求![]() 的值.
的值.
23.如图,在水平地面上有两座建筑物![]() ,其中
,其中![]() .从
.从![]() 之间的
之间的![]() 点(
点(![]() 在同一水平线上)测得
在同一水平线上)测得![]() 点,
点,![]() 点的仰角分别为
点的仰角分别为![]() 和
和![]() ,从
,从![]() 点测得
点测得![]() 点的仰角为
点的仰角为![]() .
.

(1)求![]() 的度数;
的度数;
(2)求建筑物![]() 的高度(计算过程和结果中的数据不取近似值).
的高度(计算过程和结果中的数据不取近似值).
六、本大题共2个小题,每小题12分,共24分.
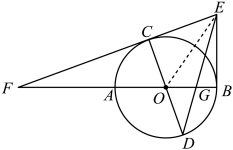
24.如图,![]() 是
是![]() 的直径,过点
的直径,过点![]() 的直线与过点
的直线与过点![]() 的切线交于点
的切线交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,且
,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
25.如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() 和点
和点![]() .
.

(1)求该抛物线的解析式;
(2)点![]() 在直线
在直线![]() 上,点
上,点![]() 在
在![]() 轴上,
轴上,![]() 是抛物线上位于第一象限的点,若四边形
是抛物线上位于第一象限的点,若四边形![]() 是正方形,求点
是正方形,求点![]() 的坐标;
的坐标;
(3)设点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在抛物线
在抛物线![]() 上,当
上,当![]() 时,
时,![]() 的最小值为3,求
的最小值为3,求![]() 的值.
的值.
参考答案
1.A
2.C
3.B
4.C
5.C
6.B
7.A
8.B
9.C
10.D
11.B
12.B
13.![]()
14.5
15.10
16.![]()
17.![]()
18.证明见解析
【详解】证明:∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() .
.
19.![]()
20.
(1)15;![]()
(2)120名
(3)![]()
21.
(1)乙种商品每件进价的年平均下降率为![]()
(2)最少购进甲种商品40件
22.
(1)![]() ;
;![]()
(2)![]()
23.
(1)![]()
(2)![]()
24.
(1)证明见解析
(2)![]()
【详解】(1)证明;如图所示,连接![]() ,
,
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,
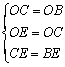 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的半径,
的半径,
∴![]() 是
是![]() 的切线;
的切线;
25.
(1)![]()
(2)![]()
(3)![]() 或
或![]()
