2025年四川自贡中考数学试题及答案
本试题卷分为第I卷(选择题)和第II卷(非选择题)两部分,共6页,满分150分
第I卷 选择题
注意事项:必须使用2B铅笔将答案标号填涂在答题卡上对应题目标号的位置上.知常改动,用橡皮擦干净后,再选涂其他答案标号.
一、选择题(共12个小题,每小题4分,共48分,在每题给出的四个选项中,只有一项是符合题目要求的)
1.若![]() ,则
,则![]() 内的数字是( )
内的数字是( )
A.![]() B.2C.4D.
B.2C.4D.![]()
2.起源于中国的围棋深受青少年喜爱.以下由黑白棋子形成的图案中,为中心对称图形的是( )
A. B.
B.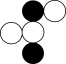 C.
C. D.
D.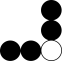
3.如图,一束平行光线穿过一张对边平行的纸板,若![]() 、则
、则![]() 的度数为( )
的度数为( )
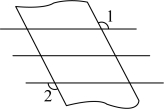
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.中国新能源汽车性能优越,近年来销售量持续攀升,2024年度销量已达到![]() 万辆.12866000用科学记数法表示为( )
万辆.12866000用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,一横一竖两块砖头放置于水平地面,其主视图为( )
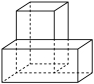
A. B.
B. C.
C.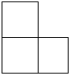 D.
D.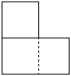
6.某校举行“唱红歌”歌咏比赛,甲、乙、丙三位选手的得分如下表所示.三项评分所占百分比如下图所示,平均分最高的是( )
选手 | 专家组评分 | 教师组评分 | 学生组评分 |
甲 | 7 | 7 | 9 |
乙 | 8 | 7 | 8 |
丙 | 7 | 8 | 8 |

A.甲B.乙C.丙D.平均分都相同
7.如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的边长为5,
的边长为5,![]() 边在
边在![]() 轴上.
轴上.![]() .若将正方形
.若将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() .得到正方形
.得到正方形![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
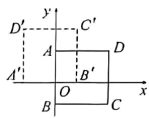
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.如图,正六边形与正方形的两邻边相交,则![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.某小区人行道地砖铺设图案如图所示.用10块相同的小平行四边形地砖拼成一个大平行四边形.若大平行四边形短边长![]() .则小地砖短边长( )
.则小地砖短边长( )

A.7cmB.8![]() C.9
C.9![]() D.
D.![]()
10.![]() 分别与
分别与![]() 相切于
相切于![]() 两点.点
两点.点![]() 在
在![]() 上,不与点
上,不与点![]() 重合.若
重合.若![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
11.如图,在平面直角坐标系中,将![]() 平移,得到
平移,得到![]() ,点
,点![]() 在坐标轴上.若
在坐标轴上.若![]() ,则点
,则点![]() 坐标为( )
坐标为( )
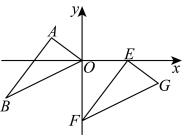
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
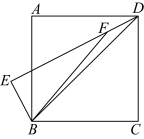
12.如图,正方形![]() 边长为6,以对角线
边长为6,以对角线![]() 为斜边作
为斜边作![]() 、
、![]() ,点
,点![]() 在
在![]() 上.连接
上.连接![]() .若
.若![]() .则
.则![]() 的最小值为( )
的最小值为( )
A.6B.6![]() C.3
C.3![]() D.4
D.4![]()
第II卷(非选择题共102分)
注意事项:必须使用0.5毫米黑色墨水签字笔在答题卡上题目所指示区域内作答,作图题可先用铅笔绘出.确认后再用0.5毫米黑色墨水签字笔描清楚,答在试题卷上无效.
二、填空题(共5个小题,每小题4分,共20分)
13.计算:![]() .
.
14.分解因式:![]() .
.
15.若![]() ,则
,则![]() 的值为 .
的值为 .
16.如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() .以点
.以点![]() 为圆心,
为圆心,![]() 的长为半径画弧,交
的长为半径画弧,交![]() 于点
于点![]() .以点
.以点![]() 为圆心.
为圆心.![]() 的长为半径画弧.交
的长为半径画弧.交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ;再以点
;再以点![]() 为圆心,
为圆心,![]() 的长为半径画弧,交
的长为半径画弧,交![]() 于点
于点![]() ,以
,以![]() 的长为半径画弧,交
的长为半径画弧,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ;又以点
;又以点![]() 为圆心……重复以上操作.则
为圆心……重复以上操作.则![]() 的长为 .
的长为 .

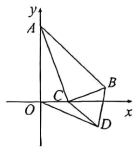
17.如图,在平面直角坐标系![]() 中,
中,![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() ,
,![]() .以
.以![]() 为边作等边
为边作等边![]() .连接
.连接![]() ,则
,则![]() 的最大值为 .
的最大值为 .
三、解答题(共8个题.共82分)
18.解不等式组:![]() ,并在数轴上表示其解集.
,并在数轴上表示其解集.
![]()
19.如图,![]() ,
,![]() .求证:
.求证:![]() .
.

20.去年暑假,小张与小李同学主动帮刘大爷掰玉米,他们各掰了36筐和30筐,两人劳动时间相同,小张平均每小时比小李多掰2筐,请问小李平均每小时掰玉米多少筐?
21.某校七年级拟组建球类课外活动兴趣班,为了解同学们的参与意向,学生会进行了随机问卷调查,要求被调查的同学在足球、篮球、乒乓球、羽毛球中任选一项.以下是依据调查数据,正在绘制中的统计图和统计表,请根据相关信息解答下列问题,
选择球类兴趣班人数条形统计图

选择球类兴趣班人数占比统计表
组别 | 球类活动兴趣班 | 占调查总人数百分比 |
A | 足球 | |
B | 篮球 | |
C | 乒乓球 | |
D | 羽毛球 |
(1)请补全上述条形统计图和占比统计表,若用扇形统计图反映选择球类活动兴趣班的人数占比,则篮球兴趣班的扇形圆心角为___________度;
(2)估计该校七年级400名学生中,选择乒乓球兴趣班的人数;
(3)若用电脑随机选择A,B,C,D四类兴趣班,请用列表或画树状图的方法,求该校七年级甲、乙两名同学都选择乒乓球兴趣班的概率
22.如图,等圆![]() 和
和![]() 相交于
相交于![]() 两点,
两点,![]() 经过
经过![]() 的圆心
的圆心![]() ,连接
,连接![]() ,作直径
,作直径![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() .
.

(1)![]() ___________度;
___________度;
(2)求证:![]() 为
为![]() 的切线;
的切线;
(3)若![]() ,求
,求![]() 上
上![]() 的长.
的长.
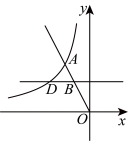
23.如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 是线段
是线段![]() 上异于端点的一点,过点
上异于端点的一点,过点![]() 作
作![]() 轴的垂线.交反比例函数的图象于点
轴的垂线.交反比例函数的图象于点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求点
,求点![]() 坐标;
坐标;
(3)双曲线![]() 关于
关于![]() 轴对称的图象为
轴对称的图象为![]() ,直接写出射线
,直接写出射线![]() 绕点
绕点![]() 旋转
旋转![]() 后与
后与![]() 的交点坐标
的交点坐标
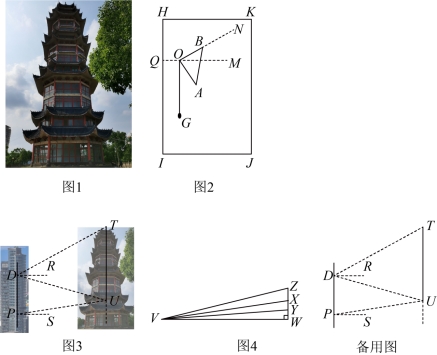
24.如图1,自贡彩灯公园内矗立着一座高塔,它见证过自贡灯会的辉煌历史.小蕊参加了测量该塔高度的课外实践活动,小组同学研讨完测量方案后,活动如下.
(1)制作工具
如图2,在矩形木板![]() 上
上![]() 点处钉上一颗小铁钉,系上细绳,绳的另一端系小重物
点处钉上一颗小铁钉,系上细绳,绳的另一端系小重物![]() ,过点
,过点![]() 画射线
画射线![]() .测量时竖放木板,当重垂线
.测量时竖放木板,当重垂线![]() 时,将等腰直角三角尺
时,将等腰直角三角尺![]() 的直角顶点
的直角顶点![]() 紧靠铁钉,绕点
紧靠铁钉,绕点![]() 转动三角尺,通过
转动三角尺,通过![]() 边瞄准目标
边瞄准目标![]() ,测量
,测量![]() 可得仰角度数.采用同样方式,可测俯角度数.
可得仰角度数.采用同样方式,可测俯角度数.
测量时,![]() 是否水平呢?小蕊产生了疑问.组长对她说:“因为
是否水平呢?小蕊产生了疑问.组长对她说:“因为![]() 始终垂直于水平面,满足
始终垂直于水平面,满足![]() 就行.”求证:
就行.”求证:![]() .
.
(2)获取数据
如图3,同学们利用制作的测量工具,在该塔对面高楼上进行了测量.已知该楼每层高3米,小蕊在15楼阳台![]() 处测得塔底
处测得塔底![]() 的仰角为
的仰角为![]() ,在25楼对应位置
,在25楼对应位置![]() 处测得塔底
处测得塔底![]() 的俯角为
的俯角为![]() ,塔顶
,塔顶![]() 的仰角为
的仰角为![]() .
.
如图4,为得到仰角与俯角的正切值,小蕊在练习本上画了一个![]() ,
,![]() ,
,![]() ,
,![]() .在边
.在边![]() 上取两点
上取两点![]() ,
,![]() ,使
,使![]() ,
,![]() ,量得
,量得![]() ,
,![]() ,
,![]() ,则
,则![]() ___________,
___________,![]() ___________,
___________,![]() ___________(结果保留小数点后两位)
___________(结果保留小数点后两位)
(3)计算塔高
请根据小蕊的数据,计算该塔高度(结果取整数).
(4)反思改进
小蕊的测量结果与该塔实际高度存在2米的误差.为减小误差,小组同学想出了许多办法.请你也帮小蕊提出两条合理的改进建议(总字数少于50字).
25.如图,在![]() 中,
中,![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() ,
,![]() 交于点
交于点![]() .
.
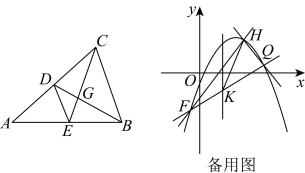
(1)若![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为___________;
的面积为___________;
(2)若![]() ,
,![]() 的最大面积为
的最大面积为![]() .设
.设![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并求
之间的函数关系式,并求![]() 的最大值;
的最大值;
(3)若(2)问中![]() 取任意实数,将函数
取任意实数,将函数![]() 的图象依次向右、向上平移1个单位长度,得到函数
的图象依次向右、向上平移1个单位长度,得到函数![]() 的图象.直线
的图象.直线![]() 交该图象于点
交该图象于点![]() ,
,![]() (
(![]() 点在
点在![]() 点左边),过点
点左边),过点![]() 的直线
的直线![]() 交该图象于另一点
交该图象于另一点![]() ,过点
,过点![]() 的直线与直线
的直线与直线![]() 交于点
交于点![]() .若
.若![]() ,试问直线
,试问直线![]() 是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由
是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由
参考答案
1.A
2.C
3.D
4.C
5.D
6.B
7.A
8.B
9.B
10.D
11.B
12.D
13.![]()
14.![]()
15.![]()
16.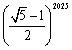
17.![]() ##
##![]()
18.![]() ,见解析
,见解析
【详解】解:![]() ,
,
由①得:![]() ,
,
由②得:![]() ,
,
在数轴上表示其解集如下:
![]()
∴不等式组的解集为:![]() .
.
19.见解析
【详解】证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
20.10筐
21.(1)补全上述条形统计图和占比统计表见解析,![]()
(2)![]() 人
人
(3)![]()
22.
(1)![]()
(2)见解析
(3)![]()
【详解】
(2)证明:如图,连接![]() ,
,

由(1)得:![]() ,
,![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为半径,
为半径,
∴![]() 为
为![]() 的切线;
的切线;
23.(1)![]()
(2)![]()
(3)射线![]() 绕点
绕点![]() 旋转
旋转![]() 后与
后与![]() 的交点坐标为
的交点坐标为![]() 或
或![]() .
.
24.
(1)见解析
(2)![]() ,
,![]() ,
,![]()
(3)50米
(4)见解析
【详解】
(1)证明:∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(4)解:提出合理建议为:①多次测量取平均值;②取角的正切值用分数.
25.(1)![]()
(2)![]() ,
,![]() 最大为
最大为![]()
(3)是,![]()
