2025年四川成都中考数学试题及答案
A卷(共100分)
第Ⅰ卷(选择题,共32分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1.如果某天中午的气温是![]() ,傍晚比中午下降了
,傍晚比中午下降了![]() ,那么傍晚的气温是( )
,那么傍晚的气温是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列几何体中,主视图和俯视图相同的是( )
A.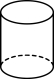 B.
B.
C.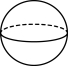 D.
D.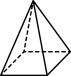
3.下列计算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.在平面直角坐标系![]() 中,点
中,点![]() 所在的象限是( )
所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
5.在第25个全国科技活动周中,某班每位学生结合自己的兴趣从元宇宙、脑机接口和人形机器人中选择一项进行深入了解,现将选择结果绘制成如下统计图表:
人数 | |
元宇宙 | 16 |
脑机接口 | a |
人形机器人 | 14 |
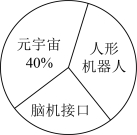
根据图表信息,表中a的值为( )
A.8B.10C.12D.15
6.中国古代数学著作《九章算术》中记载了这样一个题目:今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万.问善、恶田各几何?其大意是:今有良田1亩价值300钱;劣田7亩价值500钱.今合买良、劣田1顷(100亩),价值10000钱.问良田、劣田各有多少亩?设良田为x亩,劣田为y亩,则可列方程组为( )
A. B.
B.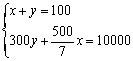
C.![]() D.
D.![]()
7.下列命题中,假命题是( )
A.矩形的对角线相等B.菱形的对角线互相垂直
C.正方形的对角线相等且互相垂直D.平行四边形的对角线相等
8.小明从家跑步到体育馆,在那里锻炼了一段时间后又跑步到书店买书,然后步行回家(小明家、书店、体育馆依次在同一直线上),如图表示的是小明离家的距离与时间的关系.下列说法正确的是( )

A.小明家到体育馆的距离为![]() B.小明在体育馆锻炼的时间为
B.小明在体育馆锻炼的时间为![]()
C.小明家到书店的距离为![]() D.小明从书店到家步行的时间为
D.小明从书店到家步行的时间为![]()
第Ⅱ卷(非选择题,共68分)
二、填空题(本大题共5个小题,每小题4分,共20分)
9.若![]() ,则
,则![]() 的值为 .
的值为 .
10.任意给一个数x,按下列程序进行计算.若输出的结果是15,则x的值为 .
![]()
11.正六边形![]() 的边长为1,则对角线
的边长为1,则对角线![]() 的长为 .
的长为 .
12.某蓄电池的电压为定值.使用此电源时,用电器的电流I(A).与电阻R(Ω)之间的函数关系为![]() ,则电流Ⅰ的值随电阻R值的增大而 (填“增大”或“减小”).
,则电流Ⅰ的值随电阻R值的增大而 (填“增大”或“减小”).
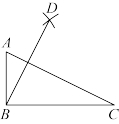
13.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .以点A为圆心,以
.以点A为圆心,以![]() 长为半径作弧;再以点C为圆心,以
长为半径作弧;再以点C为圆心,以![]() 长为半径作弧,两弧在
长为半径作弧,两弧在![]() 上方交于点D,连接
上方交于点D,连接![]() ,则
,则![]() 的长为 .
的长为 .
三、解答题(本大题共5个小题,共48分)
14.(1)计算:![]() .
.
(2)解不等式组: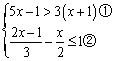
15.某公司需要经常快递物品,准备从A,B两家快递平台中选择一家作为日常使用.该公司让七位相关员工对这两家平台从物品完好度、服务态度与物流时长三项分别评分(单位:分),其中对平台A的服务态度评分为:86,88,89,91,92,95,96;对平台B的服务态度评分为:86,86,89,90,91,93,95.现将每项七个评分的平均值作为该项的得分,平台A,B各项的得分如下表:
物品完好度 | 服务态度 | 物流时长 | |
平台A | 92 | m | 90 |
平台B | 95 | n | 88 |
(1)七位员工对平台A的服务态度评分的极差(最大值与最小值的差)是________;
(2)求表格中m,n的值,并以此为依据,请判断哪家平台服务态度更好;
(3)如果公司将物品完好度、服务态度、物流时长三项的得分按![]() 的比例确定平台的最终得分,并以此为依据选择平台,请问该公司会选择哪家平台?
的比例确定平台的最终得分,并以此为依据选择平台,请问该公司会选择哪家平台?
16.在综合与实践活动中,某学习小组用无人机测量校园西门A与东门B之间的距离.如图,无人机从西门A处垂直上升至C处,在C处测得东门B的俯角为![]() ,然后沿
,然后沿![]() 方向飞行60米到达D处,在D处测得西门A的俯角为
方向飞行60米到达D处,在D处测得西门A的俯角为![]() .求校园西门A与东门B之间的距离.(结果精确到0.1米;参考数据:
.求校园西门A与东门B之间的距离.(结果精确到0.1米;参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)

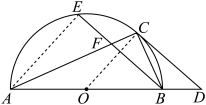
17.如图,点C在以![]() 为直径的半圆O上,连接
为直径的半圆O上,连接![]() ,过点C作半圆O的切线,交
,过点C作半圆O的切线,交![]() 的延长线于点D,在
的延长线于点D,在![]() 上取点E,使
上取点E,使![]() ,连接
,连接![]() ,交
,交![]() 于点F.
于点F.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求半圆O的半径及
,求半圆O的半径及![]() 的长.
的长.
18.如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与反比例函数
与反比例函数![]() 的图象的一个交点为
的图象的一个交点为![]() ,与x轴的交点为
,与x轴的交点为![]()

(1)求k的值;
(2)直线![]() 与反比例函数的图象在第三象限交于点C,点D在反比例函数的图象上,若
与反比例函数的图象在第三象限交于点C,点D在反比例函数的图象上,若![]() ,求直线
,求直线![]() 的函数表达式;
的函数表达式;
(3)P为x轴上一点,直线![]() 交反比例函数的图象于点E(异于A),连接
交反比例函数的图象于点E(异于A),连接![]() ,若
,若![]() 的面积为2,求点E的坐标.
的面积为2,求点E的坐标.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19.多项式![]() 加上一个单项式后,能成为一个多项式的平方,那么加上的单项式可以是 (填一个即可).
加上一个单项式后,能成为一个多项式的平方,那么加上的单项式可以是 (填一个即可).
20.从![]() ,1,2这三个数中任取两个数分别作为a,b的值,则关于x的一元二次方程
,1,2这三个数中任取两个数分别作为a,b的值,则关于x的一元二次方程![]() 有实数根的概率为 .
有实数根的概率为 .
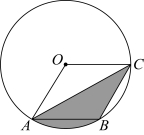
21.如图,![]() 的半径为1,A,B,C是
的半径为1,A,B,C是![]() 上的三个点.若四边形
上的三个点.若四边形![]() 为平行四边形,连接AC,则图中阴影部分的面积为 .
为平行四边形,连接AC,则图中阴影部分的面积为 .
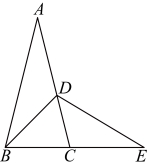
22.如图,在![]() 中,
中,![]() ,点D在
,点D在![]() 边上,
边上,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为 ;点E在
的值为 ;点E在![]() 的延长线上,连接
的延长线上,连接![]() ,若
,若![]() ,则
,则![]() 的长为
的长为
23.分子为1的真分数叫做“单位分数”,也叫“埃及分数”.古埃及人在分数计算时总是将一个分数拆分成几个单位分数之和,如:![]() .将
.将![]() 拆分成两个单位分数相加的形式为 ;一般地,对于任意奇数k(
拆分成两个单位分数相加的形式为 ;一般地,对于任意奇数k(![]() ),将
),将![]() 拆分成两个不同单位分数相加的形式为 .
拆分成两个不同单位分数相加的形式为 .
二、解答题(本大题共3个小题,共30分)
24.2025年8月7日至17日,第12届世界运动会将在成都举行,与运动会吉祥物“蜀宝”“锦仔”相关的文创产品深受大家喜爱.某文旅中心在售A,B两种吉祥物挂件,已知每个B种挂件的价格是每个A种挂件价格的![]() ,用300元购买B种挂件的数量比用200元购买A种挂件的数量多7个.
,用300元购买B种挂件的数量比用200元购买A种挂件的数量多7个.
(1)求每个A种挂件的价格;
(2)某游客计划用不超过600元购买A,B两种挂件,且购买B种挂件的数量比A种挂件的数量多5个,求该游客最多购买多少个A种挂件.
25.如图,在![]() 中,点
中,点![]() 在
在![]() 边上,点
边上,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 内,射线
内,射线![]() 交射线
交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() .
.
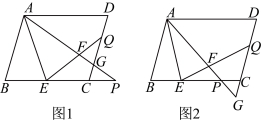
【特例感知】
(1)如图1,当![]() 时,点
时,点![]() 在
在![]() 延长线上,求证:
延长线上,求证:![]() ;
;
【问题探究】
(2)在(1)的条件下,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
【拓展延伸】
(3)如图2,当![]() 时,点
时,点![]() 在
在![]() 边上,若
边上,若![]() ,求
,求![]() 的值.(用含
的值.(用含![]() 的代数式表示)
的代数式表示)
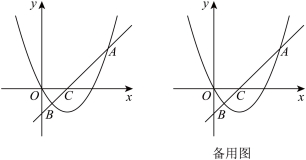
26.如图,在平面直角坐标系xOy中,抛物线![]() 过点
过点![]() ,且对称轴为直线
,且对称轴为直线![]() ,直线
,直线![]() 与抛物线交于A,B两点,与x轴交于点C.
与抛物线交于A,B两点,与x轴交于点C.
(1)求抛物线的函数表达式;
(2)当![]() 时,直线
时,直线![]() 与y轴交于点D,与直线
与y轴交于点D,与直线![]() 交于点E.若抛物线
交于点E.若抛物线![]() 与线段
与线段![]() 有公共点,求h的取值范围;
有公共点,求h的取值范围;
(3)过点C与![]() 垂直的直线交抛物线于P,Q两点,M,N分别是
垂直的直线交抛物线于P,Q两点,M,N分别是![]() ,
,![]() 的中点.试探究:当k变化时,抛物线的对称轴上是否存在定点T,使得
的中点.试探究:当k变化时,抛物线的对称轴上是否存在定点T,使得![]() 总是平分
总是平分![]() ?若存在,求出点T的坐标;若不存在,请说明理由
?若存在,求出点T的坐标;若不存在,请说明理由
参考答案
1.B
2.C
3.D
4.B
5.B
6.A
7.D
8.C
9.4
10.3
11.2
12.减小
13.![]() ##
##![]()
14.(1)3;(2)![]()
15.(1)10分
(2)![]() ,
,![]() ,平台A的服务态度更好;
,平台A的服务态度更好;
(3)该公司会选择平台B
16.校园西门A与东门B之间的距离为207.6米
17.(1)见解析
(2)半圆O的半径为2,![]()
【详解】(1)解:连接![]() ,则:
,则:![]() ,
,
∴![]() ,
,
∵过点C作半圆O的切线,交![]() 的延长线于点D,
的延长线于点D,
∴![]() ,
,
∴![]() ,
,
∵![]() 为直径,
为直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
18.(1)![]()
(2)![]()
(3)![]() 或
或![]()
19.![]() (答案不唯一)
(答案不唯一)
20.![]() ##
##![]()
21.![]()
22. 4 ![]() ##
##![]()
23. ![]()
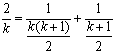
24.(1)每个A种挂件的价格为25元
(2)该游客最多购买11个A种挂件
25.(1)见解析;(2)4;(3)![]()
【详解】解:(1)由折叠的性质得:![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
26.(1)![]()
(2)![]()
(3)抛物线的对称轴上存在![]() ,使得
,使得![]() 总是平分
总是平分![]()
