2025年北京高考数学试题及答案
第一部分（选择题 共40分）
一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项．
1．集合
，则
（ ）
A．
B．
C．
D．
2．已知复数z满足
，则
（ ）
A．
B．
C．4D．8
3．双曲线
的离心率为（ ）
A．
B．
C．
D．
4．为得到函数
的图象，只需把函数
的图象上的所有点（ ）
A．横坐标变成原来的
倍，纵坐标不变B．横坐标变成原来的2倍，纵坐标不变
C．纵坐标变成原来的
倍，横坐标不变D．纵坐标变成原来的3倍，横坐标不变
5．已知
是公差不为0的等差数列，
，若
成等比数列，则
（ ）
A．
B．
C．16D．18
6．已知
，则（ ）
A．
B．
C．
D．
7．已知函数
的定义域为D，则“函数
的值域为
”是“对任意
，存在
，使得
”的（ ）
A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件
8．设函数
，若
恒成立，且
在
上存在零点，则
的最小值为（ ）
A．8B．6C．4D．3
9．在一定条件下，某人工智能大语言模型训练N个单位的数据量所需要时间
（单位：小时），其中k为常数．在此条件下，已知训练数据量N从
个单位增加到
个单位时，训练时间增加20小时；当训练数据量N从
个单位增加到
个单位时，训练时间增加（单位：小时）（ ）
A．2B．4C．20D．40
10．已知平面直角坐标系
中，
，
，设
，则
的取值范围是（ ）
A．
B．
C．
D．
第二部分（非选择题 共110分）
二、填空题共5小题，每小题5分，共25分.
11．抛物线
的顶点到焦点的距离为3，则
．
12．已知
，则
；
．
13．已知
，且
，
，写出满足条件的一组
，
．
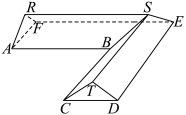
14．某科技兴趣小组通过3D打印机的一个零件可以抽象为如图所示的多面体，其中ABCDEF是一个平行多边形，平面
平面ABC，平面
平面ABC，
，
，若
，则该多面体的体积为
15．关于定义域为R的函数
，以下说法正确的有 ．
①存在在R上单调递增的函数
使得
恒成立；
②存在在R上单调递减的函数
使得
恒成立；
③使得
恒成立的函数
存在且有无穷多个；
④使得
恒成立的函数
存在且有无穷多个．
三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.
16．在
中，
．
(1)求c；
(2)在以下三个条件中选择一个作为已知，使得
存在，求BC的高．
①
；②
；③
面积为
．
17．四棱锥
中，
与
为等腰直角三角形，
，E为BC的中点．
(1)F为
的中点，G为PE的中点，证明：
面PAB；
(2)若
面ABCD，
，求AB与面PCD所成角的正弦值．
18．有一道选择题考查了一个知识点，甲、乙两校各随机抽取100人，甲校有80人答对，乙校有75人答对，用频率估计概率．
(1)从甲校随机抽取1人，求这个人做对该题目的概率．
(2)从甲、乙两校各随机抽取1人，设X为做对的人数，求恰有1人做对的概率以及X的数学期望．
(3)若甲校同学掌握这个知识点则有
的概率做对该题目，乙校同学掌握这个知识点则有
的概率做对该题目，未掌握该知识点的同学都是从四个选项里面随机选择一个，设甲校学生掌握该知识点的概率为
，乙校学生掌握该知识点的概率为
，试比较
与
的大小（结论不要求证明）
19．已知
的离心率为
，椭圆上的点到两焦点距离之和为4，
(1)求椭圆方程；
(2)设O为原点，
为椭圆上一点，直线
与直线
，
交于A，B．
与
的面积为
，比较
与
的大小．
20．函数
的定义域为
，
为
处的切线．
(1)
的最大值；
(2)
，除点A外，曲线
均在
上方；
(3)若
时，直线
过A且与
垂直，
，
分别于x轴的交点为
与
，求
的取值范围．
21．
，从M中选出n个有序数对构成一列：
．相邻两项
满足：
或
，称为k列．
(1)若k列的第一项为
，求第二项．
(2)若
为k列，且满足i为奇数时，
：i为偶数时，
；判断：
与
能否同时在
中，并说明；
(3)证明：M中所有元素都不构成k列
参考答案
1．D
2．B
3．B
4．A
5．C
6．C
7．A
8．C
9．B
10．D
11．
12． 
13． 
（答案不唯一） 
（答案不唯一）
14．
15．②③
16．(1)6
(2)答案见解析
（2）如图所示，若
存在，则设其
边上的高为
，
若选①，
，因为
，所以
，因为
，这表明此时三角形
有两个钝角，
而这是不可能的，所以此时三角形
不存在，故
边上的高也不存在；
若选②，
，由正弦定理有
，解得
，
此时
，
，
而
，
，
，
所以
，
可以唯一确定，
所以此时
也可以唯一确定，
这表明此时三角形
是存在的，且
边上的高
；
若选③，
的面积是
，则
，
解得
，由余弦定理可得
可以唯一确定，
进一步由余弦定理可得
也可以唯一确定，即
可以唯一确定，
这表明此时三角形
是存在的，且
边上的高满足：
，即
.
17．(1)证明过程见解析
(2)
【详解】（1）取PA的中点N，PB的中点M，连接FN、MN，
与
为等腰直角三角形
不妨设
，
E、F分别为BC、PD的中点，
，
，
，
，
∴四边形FGMN为平行四边形，
，
面PAB，
面PAB，
面PAB；
18．(1)
(2)
，
(3)
19．(1)
(2)
20．(1)
(2)证明见解析
(3)
【详解】
（2）因为
，所以直线
的方程为
，即
，
设
，
，
由（1）可知，
在
上单调递增，而
，
所以，当
时，
，
单调递减，
当
时，
，
单调递增，且
，
而当
时，
，所以总有
，
单调递增
故
，从而命题得证；
21．
(1)
或
(2)不能，理由见解析
(3)证明过程见解析
【详解】（1）根据题目定义可知，
或
，
若第一项为
，显然
或
不符合题意（不在集合
中），所以下一项是
或
；
（2）假设二者同时出现在
中，由于
列取反序后仍是
列，故可以不妨设
在
之前.
显然，在
列中，相邻两项的横纵坐标之和的奇偶性总是相反的，所以从
到
必定要向下一项走奇数次.
但又根据题目条件，这两个点的横坐标均在中，所以从
到
必定要向下一项走偶数次.
这导致矛盾，所以二者不能同时出现在
中.
（3）法1：若
中的所有元素构成
列，考虑
列中形如
的项，
这样的项共有
个，由题知其下一项为
，共计16个，
而
，因为只能6由2来，3只能由7来，
横、纵坐标不能同时相差4，这样下一项只能有12个点，
即对于16个
，有12个
与之相对应，矛盾．
综上，M中所有元素都无法构成
列
法2：全体元素构成一个
列，则
.
设
，
.
则
和
都包含
个元素，且
中元素的相邻项必定在
中.
如果存在至少两对相邻的项属于
，那么属于
的项的数目一定多于属于
的项的数目，
所以至多存在一对相邻的项属于
.
如果存在，则这对相邻的项的序号必定形如
和
，
否则将导致属于
的项的个数比属于
的项的个数多2，此时
.
从而这个序列的前
项中，第奇数项属于
，第偶数项属于
；
这个序列的后
项中，第奇数项属于
，第偶数项属于
.
如果不存在相邻的属于
的项，那么也可以看作上述表示在
或
的特殊情况.
这意味着必定存在
，使得
.
由于相邻两项的横纵坐标之和的奇偶性必定相反，故
中横纵坐标之和为奇数的点和横纵坐标之和为偶数的点的数量一定分别是
和
（不一定对应）.
但容易验证，
和
都包含
个横纵坐标之和为奇数的点和
个横纵坐标之和为偶数的点，所以
，得
.
从而有
.
这就得到
.
再设
，
.
则同理有
这意味着
.
从而得到
，但显然它们是不同的集合，矛盾.
所以全体元素不能构成一个
列