2025年四川高考数学试题及答案
一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.
1. 样本数据2，8，14，16，20的平均数为（ ）
A. 8B. 9C. 12D. 18
2. 已知
，则
（ ）
A. 
B. 
C. 
D. 1
3. 已知集合
则
（ ）
A. 
B. 
C. 
D. 
4. 不等式
的解集是（ ）
A. 
B. 
C. 
D. 
5. 在
中，
，
，
，则
（ ）
A. 
B. 
C. 
D. 
6. 设抛物线
焦点为
点A在C上，过A作
的准线的垂线，垂足为B，若直线BF的方程为
，则
（ ）
A. 3B. 4C. 5D. 6
7. 记
为等差数列
的前n项和，若
则
（ ）
A. 
B. 
C. 
D. 
8. 已知
，
，则
（ ）
A. 
B. 
C. 
D. 
二、多选题：本题共3小题，共18分.在每小题给出的选项中，有多项符合题目要求.
9. 记
为等比数列
前n项和，
为
的公比，
若
，则（ ）
A. 
B. 
C. 
D. 
10. 已知
是定义在R上的奇函数，且当
时，
，则（ ）
A. 
B. 当
时，
C. 
当且仅当
D. 
是
的极大值点
11. 双曲线
的左、右焦点分别是
，左、右顶点分别为
，以
为直径的圆与C的一条渐近线交于M、N两点，且
，则（ ）
A. 
B. 
C. C的离心率为
D. 当
时，四边形
的面积为
三、填空题：本题共3小题，每小题5分，共15分.
12. 已知平面向量
若
，则
___________
13. 若
是函数
的极值点，则
___________
14. 一个底面半径为
，高为
的封闭圆柱形容器（容器壁厚度忽略不计）内有两个半径相等的铁球，则铁球半径的最大值为____________
四、解答题：本题共5小题，共77分.解答应写出文字说明，证明过程或演算步骤.
15. 已知函数
．
（1）求
;
（2）设函数
，求
的值域和单调区间．
16. 已知椭圆
的离心率为
，长轴长为4．
（1）求C
方程；
（2）过点
直线l与C交于
两点，
为坐标原点，若
的面积为
，求
．
17. 如图，在四边形
中，
，F为CD的中点，点E在AB上，
，
，将四边形
沿
翻折至四边形
，使得面
与面EFCB所成的二面角为
．
（1）证明:
平面
；
（2）求面
与面
所成的二面角的正弦值．
18. 已知函数
，其中
．
（1）证明：
在区间
存在唯一的极值点和唯一的零点；
（2）设
分别为
在区间
的极值点和零点.
（i）设函数
·证明：
在区间
单调递减；
（ii）比较
与
的大小，并证明你的结论．
19. 甲、乙两人进行乒乓球练习，每个球胜者得1分，负者得0分．设每个球甲胜
概率为
，乙胜的概率为q，
，且各球的胜负相互独立，对正整数
，记
为打完k个球后甲比乙至少多得2分的概率，
为打完k个球后乙比甲至少多得2分的概率．
（1）求
（用p表示）．
（2）若
，求p．
（3）证明：对任意正整数m，
参考答案
3.考试结束后，本试卷和答题卡一并交回.
一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.
1.C | 2.A | 3.D | 4.C | 5.A | 6.C | 7.B | 8.D |
二、多选题：本题共3小题，共18分.在每小题给出的选项中，有多项符合题目要求.
9.AD | 10.ABD | 11.ACD |
三、填空题：本题共3小题，每小题5分，共15分.
12.
13.
14.
四、解答题：本题共5小题，共77分.解答应写出文字说明，证明过程或演算步骤.
15.
16.
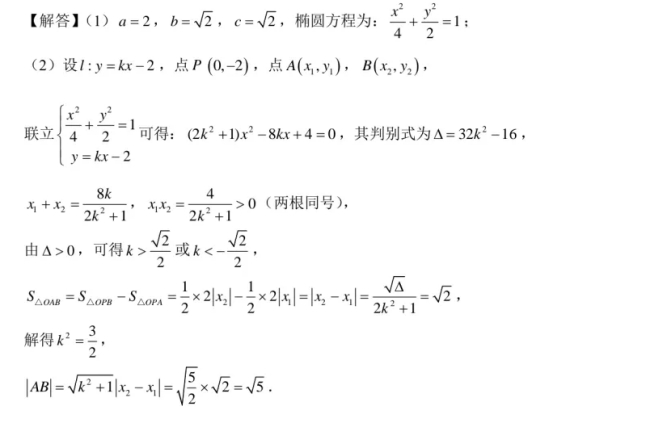
17.
18.
19.
