2024年山东淄博中考数学真题及答案
一、选择题（本大题共10小题，每题4分，共40分）
1. 下列运算结果是正数的是（ ）
A. 
B. 
C. 
D. 
2. 下列图案中，既是轴对称图形又是中心对称图形的是（ ）
A. 
B. 
C. 
D. 
3. 我国大力发展新质生产力，推动了新能源汽车产业的快速发展．据中国汽车工业协会发布的消息显示．2024年1至3月，我国新能源汽车完成出口的的值是（ ）
A. 4 B. 5 C. 6 D. 7
4. 如图，已知
，
平分
．若
，则
的度数是（ ）
A. 
B. 
C. 
D. 
5. 数学兴趣小组成员小刚对自己的学习质量进行了测试．如图是他最近五次测试成绩（满分为100分）的折线统计图，那么其平均数和方差分别是（ ）
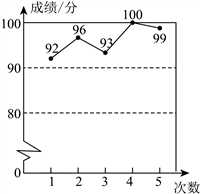
A. 95分，
B. 96分， C. 95分，10 D. 96分，10
6. 如图，在综合与实践活动课上，小强先测得教学楼在水平地面上的影长
为
．又在点
处测得该楼的顶端
的仰角是
．则用科学计算器计算教学楼高度的按键顺序正确的是（ ）
A. 
B. 
C. 
D. 
7. 《九章算术》中提到：今有户高多于广六尺八寸．两隅相去适一丈．问户高、广各几何？其大意为：已知矩形门的高比宽多6尺8寸，门的对角线长1丈，那么门的高和宽各是多少？（1丈
尺，1尺寸）若设门的高和宽分别是
尺和
尺．则下面所列方程组正确的是（ ）
A. 
B. 
C. 
D. 
8. 如图所示，在矩形
中，
，点
，
分别在边
，
上．连接
，将四边形
沿翻折，点
，
分别落在点
，
处．则
的值是（ ）
A. 2 B. 
C. 
D. 
9. 如图所示，正方形与
（其中边，
分别在，轴的正半轴上）的公共顶点在反比例函数
的图象上，直线
与，轴分别相交于点，．若这两个正方形的面积之和是
，且
．则
的值是（ ）
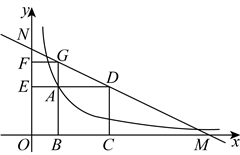
A. 5 B. 1 C. 3 D. 2
10. 某日，甲、乙两人相约在一条笔直的健身道路上锻炼．两人都从
地匀速出发，甲健步走向
地．途中偶遇一位朋友，驻足交流
后，继续以原速步行前进；乙因故比甲晚出发
，跑步到达地后立刻以原速返回，在返回途中与甲第二次相遇．下图表示甲、乙两人之间的距离
与甲出发的时间
之间的函数关系．( )
那么以下结论：
①甲、乙两人第一次相遇时，乙的锻炼用时为
；
②甲出发
时，甲、乙两人之间的距离达到最大值
；
③甲、乙两人第二次相遇的时间是在甲出发后
；
④，两地之间的距离是
．
其中正确的结论有：
A. ①②③ B. ①②④ C. ①③④ D. ②③④
二、填空题（共5小题，每题4分，共20分）
11. 计算：
__________．
12. 如图，已知，两点的坐标分别为
，
，将线段
平移得到线段
．若点的对应点是
，则点的对应点
的坐标是__________
13. 若多项式
能用完全平方公式因式分解，则
的值是__________．
14. 如图，在边长为10的菱形
中，对角线
，
相交与点
，点
在
延长线上，
与
相交与点
．若
，
，则菱形的面积为__________．
15. 如图，在平面直角坐标系中，作直线
与
轴相交于点
，与抛物线
相交于点
，连接
，
相交于点
，得
和
，若将其面积之比记为
，则
__________．
三、解答题（共8题90分）
16. 解不等式组：
并求所有整数解的和．
17. 如图，已知
，点，在线段上，且
．
请从①
；②
；③
中．选择一个合适的选项作为已知条件，使得
．
你添加的条件是：__________（只填写一个序号）
添加条件后，请证明
．
18. 化简分式：
，并求值（请从小宇和小丽的对话中确定
，
的值）
19. 希望中学做了如下表的调查报告（不完整）：
调查目的 | 了解本校学生：（1）周家务劳动的时间；（2）最喜欢的劳动课程 |
调查方式 | 随机问卷调查 |
调查对象 | 部分七年级学生（该校所有学生周家务劳动时间都在 |
调查内容 | （1）你的周家务劳动时间（单位： （2）你最喜欢的劳动课程是（必选且只选一门） A家政 B.烹饪 C.剪纸 D.园艺 E．陶艺 |
调查结果 |
|
范围内）
）是①
②
③
④
⑤
结合调查信息，回答下列问题：
（1）参与本次问卷调查的学生人数________名；在扇形统计图中，第④组所对应扇形的圆心角的度数为________度；
（2）补全周家务劳动时间的频数直方图：
（3）若该校七年级学生共有800人，请估计最喜欢“烹饪”课程的学生人数；
（4）小红和小颖分别从“家政”等五门最喜欢的劳动课程中任选一门学习，请用列表法或画树状图的方法，求两人恰好选到同一门课程的概率．
20. “我运动，我健康，我快乐！”随着人们对身心健康的关注度越来越高．某市参加健身运动的人数逐年增多，从2021年的32万人增加到2023年的50万人．
（1）求该市参加健身运动人数的年均增长率；
（2）为支持市民的健身运动，市政府决定从
公司购买某种套装健身器材．该公司规定：若购买不超过100套，每套售价1600元；若超过100套，每增加10套，售价每套可降低40元．但最低售价不得少于1000元．已知市政府向该公司支付货款24万元，求购买的这种健身器材的套数．
21. 如图，一次函数
的图象与反比例函数
的图象相交于
，
两点，与
，
轴分别相交于点
，
．且
．
（1）分别求这两个函数的表达式；
（2）以点为圆心，线段
的长为半径作弧与轴正半轴相交于点
，连接
，
．求
的面积；
（3）根据函数的图象直接写出关于的不等式
的解集．
22. 在综合与实践活动课上，小明以“圆”为主题开展研究性学习．
【操作发现】
小明作出了为（不与点，重合），连接
，然后将
绕点逆时针旋转得到
．如图①
小明发现：
与
的位置关系是__________，请说明理由：
【实践探究】
连接
，与
相交于点
．如图②，小明又发现：当
确定时，线段
的长存在最大值．
请求出当
．
时，长的最大值；
【问题解决】
在图②中，小明进一步发现：点
分线段
所成的比
与点分线段
所成的比
始终相等．请予以证明．
23. 如图，抛物线
与
轴相交于
，
两点（点
在点
的左侧），其中
，
是方程
的两个根，抛物线与
轴相交于点
．
（1）求该抛物线对应的函数表达式；
（2）已知直线
与，轴分别相交于点，
．
①设直线与
相交于点，问在第三象限内的抛物线上是否存在点
，使得
？若存在，求出点的坐标；若不存在，说明理由；
②过抛物线上一点
作直线的平行线．与抛物线相交于另一点
．设直线
，
相交于点
．连接
，
．求线段
的最小值
参考答案
一、选择题（本大题共10小题，每题4分，共40分）
【1题答案】
【答案】A
【2题答案】
【答案】C
【3题答案】
【答案】B
【4题答案】
【答案】C
【5题答案】
【答案】D
【6题答案】
【答案】A
【7题答案】
【答案】D
【8题答案】
【答案】A
【9题答案】
【答案】C
【10题答案】
【答案】B
二、填空题（共5小题，每题4分，共20分）
【11题答案】
【答案】
【12题答案】
【答案】
【13题答案】
【答案】
【14题答案】
【答案】96
【15题答案】
【答案】
三、解答题（共8题90分）
【16题答案】
【答案】
，
【17题答案】
【答案】①（或②）
【18题答案】
【答案】
；
【19题答案】
【答案】（1）100，
（2）见解析 （3）估计最喜欢“烹饪”课程的学生人数有176人
（4）
【20题答案】
【答案】（1）该市参加健身运动人数的年均增长率为
（2）购买的这种健身器材的套数为200套
【21题答案】
【答案】（1）一次函数解析式为
，反比例函数解析式为
（2）
（3）
或
【22题答案】
【答案】操作发现：
与
相切；实践探究：
；问题解决：见解析
【23题答案】
【答案】（1）
（2）①
；②线段
的最小值为