2024年广东深圳中考数学试题及答案
第一部分 选择题
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1. 下列用七巧板拼成的图案中,为中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
【答案】C
2. 如图,实数a,b,c,d在数轴上表示如下,则最小的实数为( )
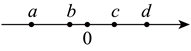
A. a B. b C. c D. d
【答案】A
3. 下列运算正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
4. 二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨),夏季(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),若从二十四个节气中选一个节气,则抽到的节气在夏季的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
5. 如图,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角![]() ,则反射光线与平面镜夹角
,则反射光线与平面镜夹角![]() 的度数为( )
的度数为( )
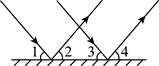
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
6. 在如图的三个图形中,根据尺规作图的痕迹,能判断射线![]() 平分
平分![]() 的是( )
的是( )
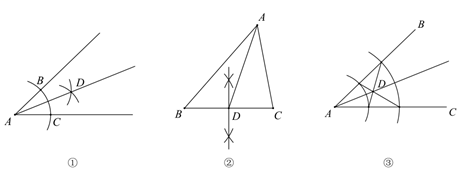
A. ①② B. ①③ C. ②③ D. 只有①
【答案】B
7. 在明朝程大位《算法统宗》中有首住店诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗的大意是:一些客人到李三公的店中住宿,如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.设该店有客房x间,房客y人,则可列方程组为( )

A.  B.
B. 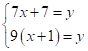
C.  D.
D. 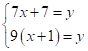
【答案】A
8. 如图,为了测量某电子厂的高度,小明用高![]() 的测量仪
的测量仪![]() 测得的仰角为
测得的仰角为![]() ,小军在小明的前面
,小军在小明的前面![]() 处用高
处用高![]() 的测量仪
的测量仪![]() 测得的仰角为
测得的仰角为![]() ,则电子厂
,则电子厂![]() 的高度为( )(参考数据:
的高度为( )(参考数据:![]() ,
,![]() ,
,![]() )
)
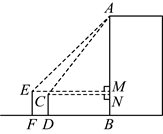
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
第二部分 非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
9. 已知一元二次方程![]()
![]() 一个根为1,则
一个根为1,则![]() ______.
______.
【答案】![]()
10. 如图所示,四边形![]() ,
,![]() ,
,![]() 均为正方形,且
均为正方形,且![]() ,
,![]() ,则正方形
,则正方形![]() 的边长可以是________.(写出一个答案即可)
的边长可以是________.(写出一个答案即可)
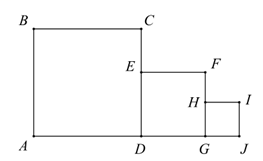
【答案】2(答案不唯一)
11. 如图,在矩形![]() 中,
中,![]() ,O为
,O为![]() 中点,
中点,![]() ,则扇形
,则扇形![]() 的面积为________.
的面积为________.
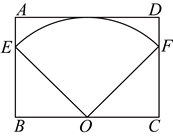
【答案】![]()
12. 如图,在平面直角坐标系中,四边形![]() 为菱形,
为菱形,![]() ,且点A落在反比例函数
,且点A落在反比例函数![]() 上,点B落在反比例函数
上,点B落在反比例函数![]() 上,则
上,则![]() ________.
________.
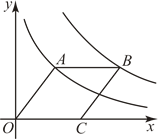
【答案】8
13. 如图,在![]() 中,
中,![]() ,
,![]() ,D
,D![]()
![]() 上一点,且满足
上一点,且满足![]() ,过D作
,过D作![]() 交
交![]() 延长线于点E,则
延长线于点E,则![]() ________.
________.
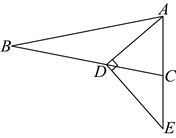
【答案】![]()
三、解答题(本题共7小题,其中第14题5分,第15题7分,第16题8分,第17题8分,第18题9分,第19题12分,第20题12分,共61分)
14. 计算: .
.
【答案】![]()
15. 先化简,再求值: ![]() ,其中
,其中 ![]()
【答案】![]() ,
,![]()
16. 据了解,“i深圳”体育场地一键预约平台是市委、市政府打造“民生幸福标杆”城市过程中,推动的惠民利民重要举措,在满足市民健身需求、激发全民健身热情、促进体育消费等方面具有重大意义.按照符合条件的学校体育场馆和社会体育场馆“应接尽接”原则,“i深圳”体育场馆一键预约平台实现了“让想运动的人找到场地,已有的体育场地得到有效利用”.
小明爸爸决定在周六上午预约一所学校的操场锻炼身体,现有A,B两所学校适合,小明收集了这两所学校过去10周周六上午的预约人数:
学校A:28,30,40,45,48,48,48,48,48,50,
学校B:
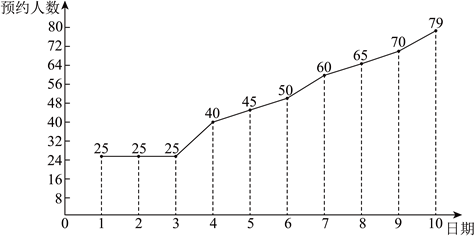
(1)
学校 | 平均数 | 众数 | 中位数 | 方差 |
A | ①________ | 48 | 83.299 | |
B | 48.4 | ②________ | ③________ | 354.04 |
(2)根据上述材料分析,小明爸爸应该预约哪所学校?请说明你的理由.
【答案】(1)①43.3;②25;③47.5
(2)小明爸爸应该预约学校A,理由见解析
17.
背景 | 【缤纷618,优惠送大家】 今年618各大电商平台促销火热,线下购物中心也亮出大招,年中大促进入“白热化”.深圳各大购物中心早在5月就开始推出618活动,进入6月更是持续加码,如图,某商场为迎接即将到来的618优惠节,采购了若干辆购物车.
| |
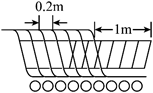
素材 | 如图为某商场叠放的购物车,右图为购物车叠放在一起的示意图,若一辆购物车车身长 |
|
问题解决 | ||
任务1 | 若某商场采购了n辆购物车,求车身总长L与购物车辆数n的表达式; | |
任务2 | 若该商场用直立电梯从一楼运输该批购物车到二楼,已知该商场的直立电梯长为 | |
任务3 | 若该商场扶手电梯一次性可以运输24辆购物车,若要运输100辆购物车,且最多只能使用电梯5次,求:共有多少种运输方案? | |
【答案】任务1:![]() ;任务2:一次性最多可以运输18台购物车;任务3:共有3种方案
;任务2:一次性最多可以运输18台购物车;任务3:共有3种方案
18. 如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 的外接圆,
的外接圆,![]() 为
为![]() 的切线,
的切线,![]() 为
为![]() 的直径,连接
的直径,连接![]() 并延长交
并延长交![]() 于点E.
于点E.
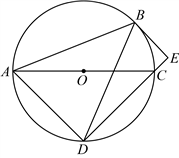
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见解析 (2)![]()
【解析】
【小问1详解】
证明:连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
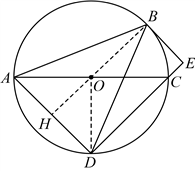
∵![]() ,
,![]() ,
,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 的切线,
的切线,
∴![]() ,
,
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ;
;
19. 为了测量抛物线的开口大小,某数学兴趣小组将两把含有刻度的直尺垂直放置,并分别以水平放置的直尺和竖直放置的直尺为x,y轴建立如图所示平面直角坐标系,该数学小组选择不同位置测量数据如下表所示,设![]() 的读数为x,
的读数为x,![]() 读数为y,抛物线的顶点为C.
读数为y,抛物线的顶点为C.
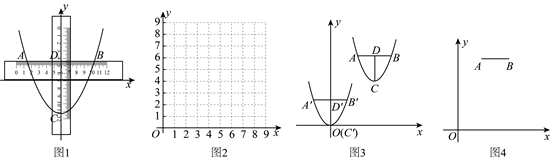
(1)(Ⅰ)列表:
① | ② | ③ | ④ | ⑤ | ⑥ | |
x | 0 | 2 | 3 | 4 | 5 | 6 |
y | 0 | 1 | 2.25 | 4 | 6.25 | 9 |
(Ⅱ)描点:请将表格中的![]() 描在图2中;
描在图2中;
(Ⅲ)连线:请用平滑的曲线在图2将上述点连接,并求出y与x的关系式;
(2)如图3所示,在平面直角坐标系中,抛物线![]() 的顶点为C,该数学兴趣小组用水平和竖直直尺测量其水平跨度为
的顶点为C,该数学兴趣小组用水平和竖直直尺测量其水平跨度为![]() ,竖直跨度为
,竖直跨度为![]() ,且
,且![]() ,
,![]() ,为了求出该抛物线的开口大小,该数学兴趣小组有如下两种方案,请选择其中一种方案,并完善过程:
,为了求出该抛物线的开口大小,该数学兴趣小组有如下两种方案,请选择其中一种方案,并完善过程:
方案一:将二次函数![]() 平移,使得顶点C与原点O重合,此时抛物线解析式
平移,使得顶点C与原点O重合,此时抛物线解析式![]()
![]() .
.
①此时点![]() 的坐标为________;
的坐标为________;
②将点![]() 坐标代入
坐标代入![]() 中,解得
中,解得![]() ________;(用含m,n的式子表示)
________;(用含m,n的式子表示)
方案二:设C点坐标为![]()
①此时点B的坐标为________;
②将点B坐标代入![]() 中解得
中解得![]() ________;(用含m,n的式子表示)
________;(用含m,n的式子表示)
(3)【应用】如图4,已知平面直角坐标系![]() 中有A,B两点,
中有A,B两点,![]() ,且
,且![]() 轴,二次函数
轴,二次函数![]() 和
和![]() 都经过A,B两点,且
都经过A,B两点,且![]() 和
和![]() 的顶点P,Q距线段
的顶点P,Q距线段![]() 的距离之和为10,求a的值.
的距离之和为10,求a的值.
【答案】(1)图见解析,![]() ;
;
(2)方案一:①![]() ;②
;②![]() ;方案二:①
;方案二:①![]() ;②
;②![]() ;
;
(3)a的值为![]() 或
或![]() .
.
【解析】
【小问1详解】
解:描点,连线,函数图象如图所示,

观察图象知,函数为二次函数,
设抛物线的解析式为![]() ,
,
由题意得 ,
,
解得![]() ,
,
∴y与x的关系式为![]() ;
;
20. 垂中平行四边形的定义如下:在平行四边形中,过一个顶点作关于不相邻的两个顶点的对角线的垂线交平行四边形的一条边,若交点是这条边的中点,则该平行四边形是“垂中平行四边形”.
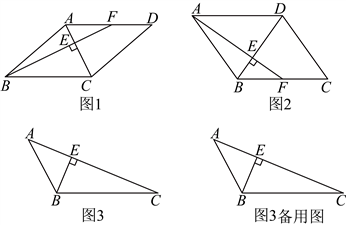
(1)如图1所示,四边形![]() 为“垂中平行四边形”,
为“垂中平行四边形”,![]() ,
,![]() ,则
,则![]() ________;
________;![]() ________;
________;
(2)如图2,若四边形![]() 为“垂中平行四边形”,且
为“垂中平行四边形”,且![]() ,猜想
,猜想![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(3)①如图3所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,请画出以
,请画出以![]() 为边的垂中平行四边形,要求:点
为边的垂中平行四边形,要求:点![]() 在垂中平行四边形的一条边上(温馨提示:不限作图工具);
在垂中平行四边形的一条边上(温馨提示:不限作图工具);
②若![]() 关于直线
关于直线![]() 对称得到
对称得到![]() ,连接
,连接![]() ,作射线
,作射线![]() 交①中所画平行四边形的边于点
交①中所画平行四边形的边于点![]() ,连接
,连接![]() ,请直接写出
,请直接写出![]() 的值.
的值.
【答案】(1)![]() ,
,![]()
(2)![]()
(3)①见解析;②![]() 或
或![]()