2024年黑龙江双鸭山中考数学试题及答案
一、选择题（每小题3分，共30分）
1. 下列计算正确的是（ ）
A. 
B. 
C. 
D. 
【答案】C
2. 下列图形既是轴对称图形又是中心对称图形的是（ ）
A. 
B. 
C. 
D. 
【答案】B
3. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图，则搭成该几何体的小正方体的个数最少是（ ）
A. 3 B. 4 C. 5 D. 6
【答案】B
4. 一组数据2，3，3，4，则这组数据的方差为（ ）
A. 1 B. 
C. 
D. 
【答案】D
5. 关于x的一元二次方程
有两个实数根，则m的取值范围是（ ）
A. 
B. 
C. 
且
D. 且
【答案】D
6. 已知关于x的分式方程
无解，则k的值为（ ）
A. 
或
B. 
C. 或
D.
【答案】A
7. 国家“双减”政策实施后，某班开展了主题为“书香满校园”的读书活动．班级决定为在活动中表现突出的同学购买笔记本和碳素笔进行奖励（两种奖品都买），其中笔记本每本3元，碳素笔每支2元，共花费28元，则共有几种购买方案（ ）
A. 5 B. 4 C. 3 D. 2
【答案】B
8. 如图，双曲线
经过A、B两点，连接
、
，过点B作
轴，垂足为D，
交于点E，且E为
的中点，则
的面积是（ ）
A. 4.5 B. 3.5 C. 3 D. 2.5
【答案】A
9. 如图，菱形
中，点
是的中点，
，垂足为
，
交于点
，
，
，则
的长为（ ）
A. 
B. 
C. 
D. 
【答案】C
10. 如图，在正方形中，点H在
边上（不与点A、D重合），
，
交正方形外角的平分线
于点F，连接
交
于点M，连接
交于点G，交
于点N，连接．则下列结论：①
；②点G是的中点；③若点H是的中点，则
；④
；⑤若
，则
，其中正确的结论是（ ）
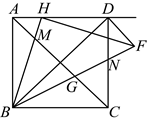
A. ①②③④ B. ①③⑤ C. ①②④⑤ D. ①②③④⑤
【答案】A
二、填空题（每小题3分，共30分）
11. 国家统计局公布数据显示，2023年我国粮食总产量是
亿斤，将亿用科学记数法表示为________．
【答案】
12. 在函数
中，自变量x的取值范围是________．
【答案】
##
13. 已知菱形
中对角线
相交于点O，添加条件_________________可使菱形成为正方形．
【答案】
或
14. 七年一班要从2名男生和3名女生中选择两名学生参加朗诵比赛，恰好选择1名男生和1名女生的概率是________．
【答案】
15. 关于x的不等式组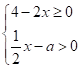
恰有3个整数解，则a的取值范围是________．
【答案】
16. 如图，
内接于
，
是直径，若
，则
________
．
【答案】
17. 若圆锥的底面半径为3，侧面积为
，则这个圆锥侧面展开图的圆心角是________
．
【答案】
18. 如图，在
中，
，
，
，
，线段
绕点
旋转，点
为
的中点，则
的最大值是________．
【答案】
19. 矩形
中，
，
，将
沿过点A的一条直线折叠，折痕交直线
于点（点P不与点B重合），点
的对称点落在矩形对角线所在的直线上，则
长为________．
【答案】
或
或10
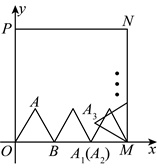
20. 如图，在平面直角坐标系中，正方形
顶点M的坐标为
，
是等边三角形，点B坐标是
，在正方形内部紧靠正方形的边（方向为
）做无滑动滚动，第一次滚动后，点A的对应点记为
，的坐标是
；第二次滚动后，的对应点记为
，的坐标是；第三次滚动后，的对应点记为
，的坐标是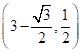
；如此下去，……，则
的坐标是________．
【答案】
三、解答题（满分60分）
21. 先化简，再求值：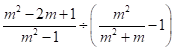
，其中
．
【答案】的
22. 如图，在正方形网格中，每个小正方形的边长都是1个单位长度，在平面直角坐标系中，
的三个顶点坐标分别为
，
，
．
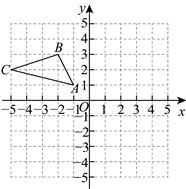
（1）画出关于y轴对称的
，并写出点
的坐标；
（2）画出绕点A逆时针旋转
后得到的
，并写出点
的坐标；
（3）在（2）的条件下，求点B旋转到点的过程中所经过的路径长（结果保留
）
【答案】（1）作图见解析，
（2）作图见解析，
（3）
【解析】
【小问1详解】
解：如图，为所求；点的坐标为
，
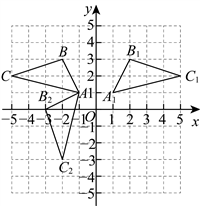
【小问2详解】
如图，
为所求；
，
【小问3详解】
，
点B旋转到点
的过程中所经过的路径长
．
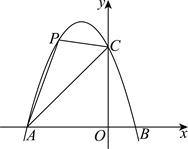
23. 如图，抛物线
与x轴交于A、B两点，与y轴交于点C，其中
，
．
（1）求抛物线的解析式．
（2）在第二象限的抛物线上是否存在一点P，使得
的面积最大．若存在，请直接写出点P坐标和的面积最大值；若不存在，请说明理由．
【答案】（1）
（2）存在，点P的坐标是
，的面积最大值是
24. 为贯彻落实教育部办公厅关于“保障学生每天校内、校外各一小时体育活动时间”的要求，某学校要求学生每天坚持体育锻炼．学校从全体男生中随机抽取了部分学生，调查他们的立定跳远成绩，整理如下不完整的频数分布表和统计图，结合下图解答下列问题：
组别 | 分组（cm） | 频数 |
A |
| 3 |
B |
| m |
C |
| 20 |
D |
| 14 |
E |
| 5 |
（1）频数分布表中
，扇形统计图中
．
（2）本次调查立定跳远成绩的中位数落在 组别．
（3）该校有600名男生，若立定跳远成绩大于200cm为合格，请估计该校立定跳远成绩合格的男生有多少人？
【答案】
（1）8，40
（2）C
（3）估计该校立定跳远成绩合格的男生有228人
25. 甲、乙两货车分别从相距
的A、B两地同时出发，甲货车从A地出发途经配货站时，停下来卸货，半小时后继续驶往B地，乙货车沿同一条公路从B地驶往A地，但乙货车到达配货站时接到紧急任务立即原路原速返回B地，结果比甲货车晚半小时到达B地．如图是甲、乙两货车距A地的距离
与行驶时间
之间的函数图象，结合图象回答下列问题：
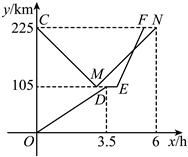
（1）甲货车到达配货站之前的速度是 
，乙货车的速度是 ；
（2）求甲货车在配货站卸货后驶往B地的过程中，甲货车距A地的距离与行驶时间之间的函数解析式；
（3）直接写出甲、乙两货车在行驶的过程中，出发多长时间甲、乙两货车与配货站的距离相等．
【答案】（1）30，40
（2）
的函数解析式是
（3）经过1.5h或
或5h甲、乙两货车与配货站的距离相等
26. 已知
是等腰三角形，
，
，
在
的内部，点M、N在
上，点M在点N的左侧，探究线段
之间的数量关系
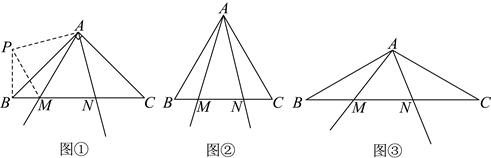
（1）如图①，当
时，探究如下：
由，
可知，将
绕点A顺时针旋转
，得到
，则
且
，连接
，易证
，可得
，在
中，
，则有
．
（2）当
时，如图②：当
时，如图③，分别写出线段
之间的数量关系，并选择图②或图③进行证明．
【答案】图②的结论是：
；图③的结论是：
；证明见解析
27. 为了增强学生的体质，某学校倡导学生在大课间开展踢毽子活动，需购买甲、乙两种品牌毽子．已知购买甲种品牌毽子10个和乙种品牌毽子5个共需200元；购买甲种品牌毽子15个和乙种品牌毽子10个共需325元．
（1）购买一个甲种品牌毽子和一个乙种品牌毽子各需要多少元？
（2）若购买甲乙两种品牌毽子共花费1000元，甲种品牌毽子数量不低于乙种品牌毽子数量的5倍且不超过乙种品牌毽子数量的16倍，则有几种购买方案？
（3）若商家每售出一个甲种品牌毽子利润是5元，每售出一个乙种品牌毽子利润是4元，在（2）的条件下，学校如何购买毽子商家获得利润最大？最大利润是多少元？
【答案】（1）购买一个甲种品牌毽子需15元，购买一个乙种品牌毽子需10元
（2）共有3种购买方案
（3）学校购买甲种品牌毽子60个，购买乙种品牌毽子10个，商家获得利润最大，最大利润是340元
28. 如图，在平面直角坐标系中，等边三角形
的边
在x轴上，点A在第一象限，
的长度是一元二次方程
的根，动点P从点O出发以每秒2个单位长度的速度沿折线
运动，动点Q从点O出发以每秒3个单位长度的速度沿折线
运动，P、Q两点同时出发，相遇时停止运动．设运动时间为t秒（
），
的面积为S
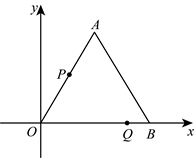
（1）求点A的坐标；
（2）求S与t的函数关系式；
（3）在（2）的条件下，当
时，点M在y轴上，坐标平面内是否存在点N，使得以点O、P、M、N为顶点的四边形是菱形．若存在，直接写出点N的坐标；若不存在，说明理由．
【答案】（1）点A的坐标为
（2）
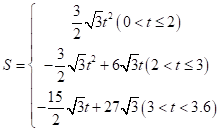
（3）存在，
，
，
，