2024年四川广元中考数学试题及答案
第Ⅰ卷 选择题(共30分)
一、选择题(每小题给出的四个选项中,只有一个符合题意.每小题3分,共30分)
1. 将![]() 在数轴上对应的点向右平移2个单位,则此时该点对应的数是( )
在数轴上对应的点向右平移2个单位,则此时该点对应的数是( )
![]()
A. ![]() B. 1 C.
B. 1 C. ![]() D. 3
D. 3
2. 下列计算正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 一个几何体如图水平放置,它的俯视图是( )

A.  B.
B.  C.
C.  D.
D. 
4. 在“五·四”文艺晚会节目评选中,某班选送的节目得分如下:91,96,95,92,94,95,95,分析这组数据,下列说法错误的是( )
A. 中位数是95 B. 方差是3 C. 众数是95 D. 平均数是94
5. 如图,已知四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() 为
为![]() 延长线上一点,
延长线上一点,![]() ,则
,则![]() 等于( )
等于( )
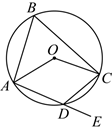
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 如果单项式![]() 与单项式
与单项式![]() 的和仍是一个单项式,则在平面直角坐标系中点
的和仍是一个单项式,则在平面直角坐标系中点![]() 在( )
在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
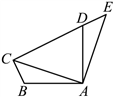
7. 如图,将![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() 得到
得到![]() ,点B,C的对应点分别为点D,E,连接
,点B,C的对应点分别为点D,E,连接![]() ,点D恰好落在线段
,点D恰好落在线段![]() 上,若
上,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
8. 我市把提升城市园林绿化水平作为推进城市更新行动的有效抓手,从2023年开始通过拆违建绿、见缝插绿等方式在全域打造多个小而美的“口袋公园”.现需要购买A、B两种绿植,已知A种绿植单价是B种绿植单价的3倍,用6750元购买的A种绿植比用3000元购买的B种绿植少50株.设B种绿植单价是x元,则可列方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
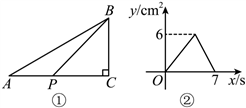
9. 如图①,在![]() 中,
中,![]() ,点P从点A出发沿A→C→B以1
,点P从点A出发沿A→C→B以1![]() 的速度匀速运动至点B,图②是点P运动时,
的速度匀速运动至点B,图②是点P运动时,![]() 的面积
的面积![]() 随时间x(s)变化的函数图象,则该三角形的斜边
随时间x(s)变化的函数图象,则该三角形的斜边![]() 的长为( )
的长为( )
A. 5 B. 7 C. ![]() D.
D. ![]()
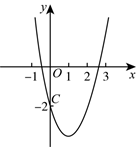
10. 如图,已知抛物线![]() 过点
过点![]() 与x轴交点的横坐标分别为
与x轴交点的横坐标分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,则下列结论:
,则下列结论:
①![]() ;
;
②方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
③![]() ;
;
④![]() ;
;
⑤![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
第Ⅱ卷 非选择题(共120分)
二、填空题(把正确答案直接写在答题卡对应题目的横线上,每小题4分,共24分)
11. 分解因式:![]() ___________________________________.
___________________________________.
12. 2023年10月诺贝尔物理学奖授予三位“追光”科学家,以表彰他们“为研究物质中的电子动力学而产生阿秒光脉冲的实验方法”.什么是阿秒?1阿秒是![]() 秒,也就是十亿分之一秒的十亿分之一.目前世界上最短的单个阿秒光学脉冲是43阿秒.将43阿秒用科学记数法表示为______秒.
秒,也就是十亿分之一秒的十亿分之一.目前世界上最短的单个阿秒光学脉冲是43阿秒.将43阿秒用科学记数法表示为______秒.
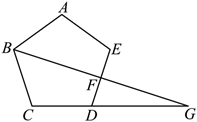
13. 点F是正五边形![]() 边
边![]() 的中点,连接
的中点,连接![]() 并延长与
并延长与![]() 延长线交于点G,则
延长线交于点G,则![]() 的度数为______.
的度数为______.
14. 若点![]() 满足
满足![]() ,则称点Q为“美好点”,写出一个“美好点”的坐标______.
,则称点Q为“美好点”,写出一个“美好点”的坐标______.
15. 已知![]() 与
与![]() 的图象交于点
的图象交于点![]() ,点B为y轴上一点,将
,点B为y轴上一点,将![]() 沿
沿![]() 翻折,使点B恰好落在
翻折,使点B恰好落在![]() 上点C处,则B点坐标为______.
上点C处,则B点坐标为______.

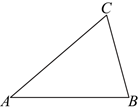
16. 如图,在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的最大值为______
的最大值为______
三、解答题(要求写出必要的解答步骤或证明过程.共96分)
17. 计算:![]() .
.
18. 先化简,再求值:![]() ,其中a,b满足
,其中a,b满足![]() .
.
19. 如图,已知矩形![]() .
.
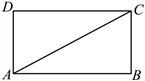
(1)尺规作图:作对角线![]() 的垂直平分线,交
的垂直平分线,交![]() 于点E,交
于点E,交![]() 于点F;(不写作法,保留作图痕迹)
于点F;(不写作法,保留作图痕迹)
(2)连接![]() .求证:四边形的菱形.
.求证:四边形的菱形.
20. 广元市开展“蜀道少年”选拔活动,旨在让更多的青少年关注蜀道、了解蜀道、热爱蜀道、宣传蜀道,进一步挖掘和传承古蜀道文化、普及蜀道知识.为此某校开展了“蜀道文化知识竞赛”活动,并从全校学生中抽取了若干学生的竞赛成绩进行整理、描述和分析(竞赛成绩用x表示,总分为100分,共分成五个等级:A:![]() ;B:
;B:![]() ;C:
;C:![]() ;D:
;D:![]() ;E:
;E:![]() ).并绘制了如下尚不完整的统计图.
).并绘制了如下尚不完整的统计图.
抽取学生成绩等级人数统计表
等级 | A | B | C | D | E |
人数 | m | 27 | 30 | 12 | 6 |
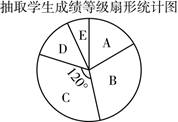
其中扇形图中C等级区域所对应的扇形的圆心角的度数是![]() .
.
(1)样本容量为______,![]() ______;
______;
(2)全校1200名学生中,请估计A等级的人数;
(3)全校有5名学生得满分,七年级1人,八年级2人,九年级2人,从这5名学生中任意选择两人在国旗下分享自己与蜀道的故事,请你用画树状图或列表的方法,求这两人来自同一个年级的概率.
21. 小明从科普读物中了解到,光从真空射入介质发生折射时,入射角![]() 的正弦值与折射角
的正弦值与折射角![]() 的正弦值的比值
的正弦值的比值![]() 叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为![]() ,折射角为
,折射角为![]() ,且
,且![]() ,
,![]() ,求该介质的折射率;
,求该介质的折射率;
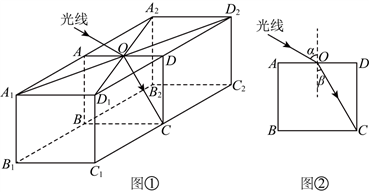
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A,B,C,D分别是长方体棱的中点,若光线经真空从矩形![]() 对角线交点O处射入,其折射光线恰好从点C处射出.如图②,已知
对角线交点O处射入,其折射光线恰好从点C处射出.如图②,已知![]() ,
,![]() ,求截面
,求截面![]() 的面积.
的面积.
22. 近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售价如下表:
价格/类别 | 短款 | 长款 |
进货价(元/件) | 80 | 90 |
销售价(元/件) | 100 | 120 |
(1)该服装店第一次用4300元购进长、短两款服装共50件,求两款服装分别购进的件数;
(2)第一次购进的两款服装售完后,该服装店计划再次购进长、短两款服装共200件(进货价和销售价都不变),且第二次进货总价不高于16800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
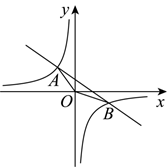
23. 如图,已知反比例函数![]() 和一次函数
和一次函数![]() 的图象相交于点
的图象相交于点![]() ,
,![]() 两点,O为坐标原点,连接
两点,O为坐标原点,连接![]() ,
,![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)当![]() 时,请结合图象直接写出自变量x的取值范围;
时,请结合图象直接写出自变量x的取值范围;
(3)求![]() 的面积.
的面积.
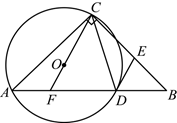
24. 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 经过A、C两点,交
经过A、C两点,交![]() 于点D,
于点D,![]() 的延长线交
的延长线交![]() 于点F,
于点F,![]() 交
交![]() 于点E.
于点E.
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
25. 数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决
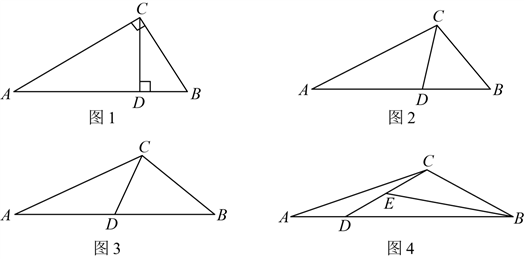
在![]() 中,点
中,点![]() 为边
为边![]() 上一点,连接
上一点,连接![]() .
.
(1)初步探究
如图2,若![]() ,求证:
,求证:![]() ;
;
(2)尝试应用
如图3,在(1)的条件下,若点![]() 为
为![]() 中点,
中点,![]() ,求
,求![]() 的长;
的长;
(3)创新提升
如图4,点![]() 为的长.
为的长.
26. 在平面直角坐标系xOy中,已知抛物线F:![]() 经过点
经过点![]() ,与y轴交于点
,与y轴交于点![]() .
.

(1)求抛物线的函数表达式;
(2)在直线![]() 上方抛物线上有一动点C,连接
上方抛物线上有一动点C,连接![]() 交
交![]() 于点D,求
于点D,求![]() 的最大值及此时点C的坐标;
的最大值及此时点C的坐标;
(3)作抛物线F关于直线![]() 上一点的对称图象
上一点的对称图象![]() ,抛物线F与
,抛物线F与![]() 只有一个公共点E(点E在y轴右侧),G为直线
只有一个公共点E(点E在y轴右侧),G为直线![]() 上一点,H为抛物线
上一点,H为抛物线![]() 对称轴上一点,若以B,E,G,H为顶点的四边形是平行四边形,求G点坐标
对称轴上一点,若以B,E,G,H为顶点的四边形是平行四边形,求G点坐标
参考答案
第Ⅰ卷 选择题(共30分)
一、选择题(每小题给出的四个选项中,只有一个符合题意.每小题3分,共30分)
【1题答案】
【答案】B
【2题答案】
【答案】D
【3题答案】
【答案】C
【4题答案】
【答案】B
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】A
【8题答案】
【答案】C
【9题答案】
【答案】A
【10题答案】
【答案】C
第Ⅱ卷 非选择题(共120分)
二、填空题(把正确答案直接写在答题卡对应题目的横线上,每小题4分,共24分)
【11题答案】
【答案】![]() ##
##![]()
【12题答案】
【答案】![]()
【13题答案】
【答案】![]() ##18度
##18度
【14题答案】
【答案】![]() (答案不唯一)
(答案不唯一)
【15题答案】
【答案】![]()
【16题答案】
【答案】![]()
三、解答题(要求写出必要的解答步骤或证明过程.共96分)
【17题答案】
【答案】![]()
【18题答案】
【答案】![]() ,
,![]()
【19题答案】
【答案】(1)见解析;
(2)见解析.
【20题答案】
【答案】(1)90,15;
(2)200; (3)![]() .
.
【21题答案】
【答案】(1)![]() ;
;
(2)![]() .
.
【22题答案】
【答案】(1)长款服装购进30件,短款服装购进20件;
(2)当购进120件短款服装,80件长款服装时有最大利润,最大利润是4800元.
【23题答案】
【答案】(1)![]() ;
;![]()
(2)![]() 或
或![]()
(3)![]()
【24题答案】
【答案】(1)证明见解析;
(2)![]() .
.
【25题答案】
【答案】(1)证明见解析
(2)![]()
(3)![]()
【26题答案】
【答案】(1)![]() ;
;
(2)最大值为![]() ,C的坐标为
,C的坐标为![]() ;
;
(3)点G的坐标为![]() ,
,![]() ,
,![]()
