2024年北京中考数学试题及答案
第一部分 选择题
一、选择题(共16分,每题2分)
第1-8题均有四个选项,符合题意的选项只有一个
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
B. C.
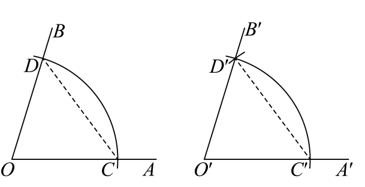
C. D.
D.
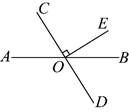
2.如图,直线![]() 和
和![]() 相交于点
相交于点![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的大小为( )
的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.实数![]() ,
,![]() 在数轴上的对应点的位置如图所示,下列结论中正确的是( )
在数轴上的对应点的位置如图所示,下列结论中正确的是( )
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若关于![]() 的一元二次方程
的一元二次方程![]() 有两个相等的实数根,则实数
有两个相等的实数根,则实数![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.4 D.16
C.4 D.16
5.不透明的袋子中装有一个红色小球和一个白色小球,除颜色外两个小球无其他差别.从中随机取出一个小球后,放回并摇匀,再从中随机取出一个小球,则两次都取到白色小球的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.为助力数字经济发展,北京积极推进多个公共算力中心的建设.北京数字经济算力中心日前已部署上架和调试的设备的算力为![]() Flops(Flops是计算机系统算力的一种度量单位),整体投产后,累计实现的算力将是日前已部署上架和调试的设备的算力的5倍,达到
Flops(Flops是计算机系统算力的一种度量单位),整体投产后,累计实现的算力将是日前已部署上架和调试的设备的算力的5倍,达到![]() Flops,则
Flops,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.下面是“作一个角使其等于![]() ”的尺规作图方法
”的尺规作图方法
(1)如图,以点 (2)作射线 (3)过点
|
上述方法通过判定![]() 得到
得到![]() ,其中判定
,其中判定![]() 的依据是( )
的依据是( )
A.三边分别相等的两个三角形全等
B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
8.如图,在菱形![]() 中,
中,![]() ,
,![]() 为对角线的交点.将菱形
为对角线的交点.将菱形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到菱形
得到菱形![]() ,两个菱形的公共点为
,两个菱形的公共点为![]() ,
,![]() ,
,![]() ,
,![]() .对八边形
.对八边形![]() 给出下面四个结论:
给出下面四个结论:
①该八边形各边长都相等;
②该八边形各内角都相等;
③点![]() 到该八边形各顶点的距离都相等;
到该八边形各顶点的距离都相等;
④点![]() 到该八边形各边所在直线的距离都相等。
到该八边形各边所在直线的距离都相等。
上述结论中,所有正确结论的序号是( )

A.①③ B.①④ C.②③ D.②④
第二部分 非选择题
二、填空题(共16分,每题2分)
9.若![]() 在实数范围内有意义,则实数
在实数范围内有意义,则实数![]() 的取值范围是 .
的取值范围是 .
10.分解因式:![]() .
.
11.方程![]() 的解为 .
的解为 .
12.在平面直角坐标系![]() 中,若函数
中,若函数![]() 的图象经过点
的图象经过点![]() 和
和![]() ,则
,则![]() 的值是 .
的值是 .
13.某厂加工了200个工件,质检员从中随机抽取10个工件检测了它们的质量(单位:g),得到的数据如下:
50.03 49.98 50.00 49.99 50.02
49.99 50.01 49.97 50.00 50.02
当一个工件的质量![]() (单位:g)满足
(单位:g)满足![]() 时,评定该工件为一等品.根据以上数据,估计这200个工件中一等品的个数是 .
时,评定该工件为一等品.根据以上数据,估计这200个工件中一等品的个数是 .
14.如图,【
15.如图,在正方形![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的面积为 .
的面积为 .
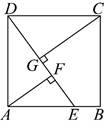
16.联欢会有A,B,C,D四个节目需要彩排.所有演员到场后节目彩排开始。一个节目彩排完毕,下一个节目彩排立即开始.每个节目的演员人数和彩排时长(单位:min)如下:
节目 | A | B | C | D |
演员人数 | 10 | 2 | 10 | 1 |
彩排时长 | 30 | 10 | 20 | 10 |
已知每位演员只参演一个节目.一位演员的候场时间是指从第一个彩排的节目彩排开始到这位演员参演的节目彩排开始的时间间隔(不考虑换场时间等其他因素)。
若节目按“![]() ”的先后顺序彩排,则节目D的演员的候场时间为 min;
”的先后顺序彩排,则节目D的演员的候场时间为 min;
若使这23位演员的候场时间之和最小,则节目应按 的先后顺序彩排
三、解答题(共68分,第17-19题每题5分,第20-21题每题6分,第22-23题每题5分,第24题6分,第25题5分,第26题6分,第27-28题每题7分)
解答应写出文字说明、演算步骤或证明过程.
17.计算:![]()
18.解不等式组: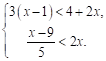
19.已知![]() ,求代数式
,求代数式![]() 的值.
的值.
20.如图,在四边形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() .
.
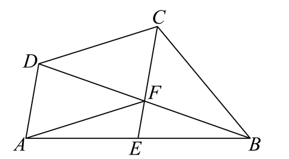
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
21.为防治污染,保护和改善生态环境,自2023年7月1日起,我国全面实施汽车国六排放标准6b阶段(以下简称“标准”).对某型号汽车,“标准”要求![]() 类物质排放量不超过的,
类物质排放量不超过的,![]() 两类物质排放量之和不超过的,
两类物质排放量之和不超过的,![]() 两类物质排放量之和原为的类物质排放量降低了
两类物质排放量之和原为的类物质排放量降低了![]() ,
,
![]() 类物质排放量降低了
类物质排放量降低了![]() ,
,![]() ,
,![]() 两类物质排放量之和为的类物质排放量是否符合“标准”,并说明理由.
两类物质排放量之和为的类物质排放量是否符合“标准”,并说明理由.
22.在平面直角坐标系![]() 中,函数
中,函数![]() 与
与![]() 的图象交于点
的图象交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)当![]() 时,对于
时,对于![]() 的每一个值,函数
的每一个值,函数![]() 的值既大于函数
的值既大于函数![]() 的值,也大于函数
的值,也大于函数![]() 的值,直接写出
的值,直接写出![]() 的取值范围.
的取值范围.
23.某学校举办的“青春飞扬”主题演讲比赛分为初赛和决赛两个阶段.
(1)初赛由![]() 名数师评委和
名数师评委和![]() 名学生评委给每位选手打分(百分制)
名学生评委给每位选手打分(百分制)![]() 对评委给某位选手的打分进行整理、描述和分析.下面给出了部分信息.
对评委给某位选手的打分进行整理、描述和分析.下面给出了部分信息.
![]() .教师评委打分:
.教师评委打分:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .学生评委打分的频数分布直方图如下(数据分6组:第1组
.学生评委打分的频数分布直方图如下(数据分6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ):
):
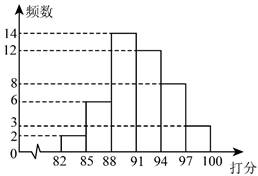
![]() .评委打分的平均数、中位数、众数如下:
.评委打分的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
教师评委 |
|
|
|
学生评委 |
|
|
|
根据以上信息,回答下列问题:
①![]() 的值为___________,
的值为___________,![]() 的值位于学生评委打分数据分组的第__________组;
的值位于学生评委打分数据分组的第__________组;
②若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分的平均数为![]() ,则
,则![]() ___________
___________![]() (填“
(填“![]() ”“
”“![]() ”或“
”或“![]() ”);
”);
(2)决赛由5名专业评委给每位选手打分(百分制).对每位选手,计算5名专业评委给其打分的平均数和方差.平均数较大的选手排序靠前,若平均数相同,则方差较小的选手排序靠前,5名专业评委给进入决赛的甲、乙、丙三位选手的打分如下:
评委1 | 评委2 | 评委3 | 评委4 | 评委5 | |
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
丙 |
|
|
|
|
|
若丙在甲、乙、丙三位选手中的排序居中,则这三位选手中排序最靠前的是____________,表中![]() (
(![]() 为整数)的值为____________.
为整数)的值为____________.
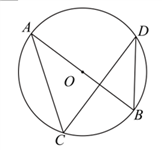
24.如图,![]() 是是,
是是,![]() 在
在![]() 上,
上,![]() 平分
平分![]() .
.
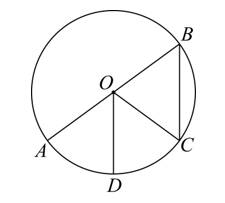
(1)求证:![]() ;
;
(2)延长![]() 交是,连接
交是,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,
,![]() ,求
,求![]() 半径的长
半径的长
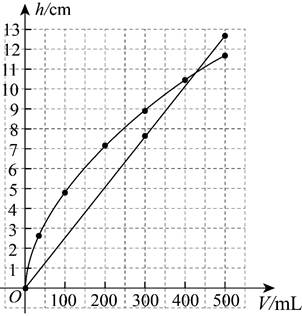
25.小云有一个圆柱形水杯(记为1号杯),在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来,新水杯(记为2号杯)示意图如下,

当1号杯和2号杯中都有![]() mL水时,小云分别记录了1号杯的水面高度
mL水时,小云分别记录了1号杯的水面高度![]() (单位:cm)和2号杯的水面高度
(单位:cm)和2号杯的水面高度![]() (单位:cm),部分数据如下:
(单位:cm),部分数据如下:
| 0 | 40 | 100 | 200 | 300 | 400 | 500 |
| 0 | 2.5 | 5.0 | 7.5 | 10.0 | 12.5 | |
| 0 | 2.8 | 4.8 | 7.2 | 8.9 | 10.5 | 11.8 |
(1)补全表格(结果保留小数点后一位);
(2)通过分析数据,发现可以用函数刻画![]() 与
与![]() ,
,![]() 与
与![]() 之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
之间的关系.在给出的平面直角坐标系中,画出这两个函数的图象;
(3)根据以上数据与函数图象,解决下列问题:
①当1号杯和2号杯中都有320mL水时,2号杯的水面高度与1号杯的水面高度的差约为___________cm(结果保留小数点后一位);
②在①的条件下,将2号杯中的一都分水倒入1号杯中,当两个水杯的水面高度相同时,其水面高度约为___________cm(结果保留小数点后一位).
26.在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(2)已知![]() 和
和![]() 是抛物线上的两点.若对于
是抛物线上的两点.若对于![]() ,
,![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
27.已知![]() ,点
,点![]() ,是分别在射线
,是分别在射线![]() ,
,![]() 上,将线段
上,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,过点
,过点![]() 作
作![]() 的垂线交射线
的垂线交射线![]() 于点
于点![]()
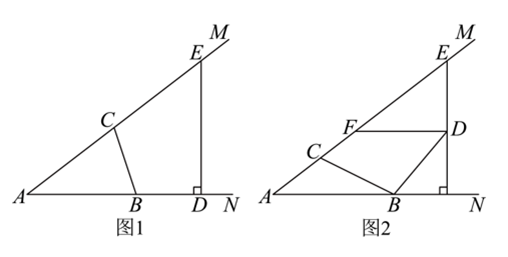
(1)如图1,当点![]() 在射线
在射线![]() 上时,求证:是是
上时,求证:是是![]() 的中点;
的中点;
(2)如图2,当点![]() 在
在![]() 内部时,作
内部时,作![]() ,交射线
,交射线![]() 于点
于点![]() ,用等式表示线段
,用等式表示线段![]() 与
与![]() 的数量关系,并证明。
的数量关系,并证明。
28.在平面直角坐标系是,给出如下定义:若点是关于直线![]() 的对称点
的对称点![]() 在是是弦
在是是弦![]() 的“
的“![]() 可及点”.
可及点”.

(1)如图,点![]() ,
,![]() .
.
①在点![]() ,
,![]() ,
,![]() 中,点___________是弦
中,点___________是弦![]() 的“
的“![]() 可及点”,其中
可及点”,其中![]() ____________
____________![]() ;
;
②若点![]() 是弦
是弦![]() 的“
的“![]() ?p暗恪保虻?img height="15" src="//img.985ks.com/images_new/img_default_show.png" data-src="//img.985ks.com/uploadfile/images/2024/0626/17194050894450224.png" width="15"/>的横坐标的最大值为__________;
?p暗恪保虻?img height="15" src="//img.985ks.com/images_new/img_default_show.png" data-src="//img.985ks.com/uploadfile/images/2024/0626/17194050894450224.png" width="15"/>的横坐标的最大值为__________;
(2)已知![]() 是直线
是直线![]() 上一点,且存<p
上一点,且存<p![]() 的弦
的弦![]() ,使得点
,使得点![]() 是弦
是弦![]() 的“
的“![]() 可及点”.记点
可及点”.记点![]() 的横坐标为
的横坐标为![]() ,直接写出
,直接写出![]() 的取值范围
的取值范围
参考答案
1.B
2.B
3.C
4.C
5.D
6.D
7.A
8.B
9.![]()
10.![]()
11.![]()
12.0
13.160
14.55
15.![]()
16. 60 ![]()
17.![]()
18.![]()
19.3
20.(1)见详解
(2)![]()
【详解】(1)证明:∵![]() 是
是![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 为平行四边形;
为平行四边形;
21.符合,理由见详解
【详解】解:设技术改进后该汽车的A类物质排放量为![]() ,则B类类物质排放量为
,则B类类物质排放量为![]() ,
,
由题意得:![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴这次技术改进后该汽车的![]() 类物质排放量是符合“标准”
类物质排放量是符合“标准”
22.(1)![]()
(2)![]()
23.(1)①![]() ,
,![]() ;②
;②![]()
(2)甲,![]()
24.(1)见解析
(2)![]()
【详解】(1)根据题意,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
25.(1)1.0
(2)见详解
(3)1.2,8.5
【详解】
(2)解:如图所示,即为所画图像,
26.(1)![]() ;
;
(2)![]() 或
或![]() .
.
27.(1)见详解
(2)![]()
【详解】
(1)证明:连接![]() ,
,
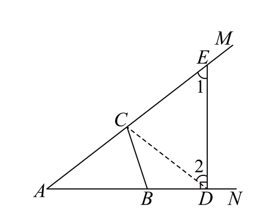
由题意得:![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点是是![]() 的中点;
的中点;
28.
(1)①![]() ,45;②
,45;②![]()
(2)![]() 或
或![]()