2024年四川德阳中考数学真题及答案

2024年四川德阳中考数学真题及答案

第Ⅰ卷（选择题，共36分）

一、选择题（本大题共12个小题，每小题3分，共36分，在每小题给出的四个选项中，有且仅有一项是符合题目要求的．）

1．下列四个数中，比小的数是（    ）

A．0                B．              C．              D．

2．下列计算正确的是（    ）

A．                            B．

C．                       D．

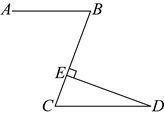
3．如图是某机械加工厂加工的一种零件的示意图，其中，，则等于（    ）

A．              B．             C．              D．

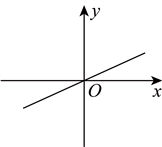
4．正比例函数的图象如图所示，则的值可能是（    ）

A．               B．             C．               D．

5．分式方程的解是（    ）

A．3                B．2                C．               D．

6．为了推进“阳光体育”，学校积极开展球类运动，在一次定点投篮测试中，每人投篮5次，七年级某班统计全班50名学生投中的次数，并记录如下：

表格中有两处数据不小心被墨汁遮盖了，下列关于投中次数的统计量中可以确定的是（    ）

A．平均数           B．中位数           C．众数             D．方差

7．走马灯，又称仙音烛，据史料记载，走马灯的历史起源于隋唐时期，盛行于宋代，是中国特色工艺品，常见于除夕、元宵、中秋等节日，在一次综合实践活动中，一同学用如图所示的纸片，沿折痕折合成一个棱锥形的“走马灯”，正方形做底，侧面有一个三角形面上写了“祥”字，当灯旋转时，正好看到“吉祥如意”的字样．则在A、B、C处依次写上的字可以是（    ）

A．吉  如  意   B．意  吉  如   C．吉  意  如   D．意  如  吉

8．已知，正六边形的面积为，则正六边形的边长为（    ）

A．1                B．              C．2                D．4

9．将一组数，按以下方式进行排列：

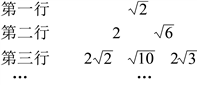
则第八行左起第1个数是（    ）

A．             B．             C．             D．

10．某校学生开展综合实践活动，测量一建筑物的高度，在建筑物旁边有一高度为10米的小楼房，小李同学在小楼房楼底处测得处的仰角为，在小楼房楼顶处测得处的仰角为．（在同一平面内，在同一水平面上），则建筑物的高为（    ）米

A．20               B．15               C．12               D．

11．宽与长的比是的矩形叫黄金矩形，黄金矩形给我们以协调的美感，世界各国许多著名建筑为取得最佳的视觉效果，都采用了黄金矩形的设计．已知四边形是黄金矩形．，点是边上一点，则满足的点的个数为（    ）

A．3                B．2                C．1                D．0

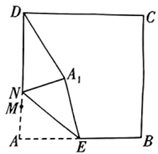
12．一次折纸实践活动中，小王同学准备了一张边长为4（单位：）的正方形纸片，他在边和上分别取点和点，使，又在线段上任取一点（点可与端点重合），再将沿所在直线折叠得到，随后连接．小王同学通过多次实践得到以下结论：

①当点在线段上运动时，点在以为圆心的圆弧上运动；

②当达到最大值时，到直线的距离达到最大；

③的最小值为；

④达到最小值时，．

你认为小王同学得到的结论正确的个数是（    ）

A．1                B．2                C．3                D．4

第Ⅱ卷（非选择题，共114分）

二、填空题（本大题共6个小题，每小题4分，共24分，将答案填在答题卡对应的题号后的横线上）

13．化简：＝          ．

14．若一个多项式加上，结果是，则这个多项式为      ．

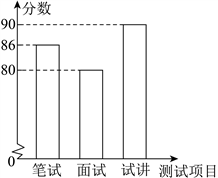
15．某校拟招聘一名优秀的数学教师，设置了笔试、面试、试讲三项水平测试，综合成绩按照笔试占，面试占，试讲占进行计算，小徐的三项测试成绩如图所示，则她的综合成绩为      分．

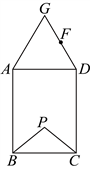
16．如图，四边形是矩形，是正三角形，点是的中点，点是矩形内一点，且是以为底的等腰三角形，则的面积与的面积的比值是      ．

17．数学活动课上，甲组同学给乙组同学出示了一个探究问题：把数字1至8分别填入如图的八个圆圈内，使得任意两个有线段相连的圆圈内的数字之差的绝对值不等于1．经过探究后，乙组的小高同学填出了图中两个中心圆圈的数字a、b，你认为a可以是      （填上一个数字即可）

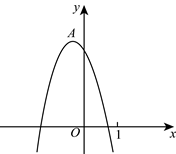
18．如图，抛物线的顶点的坐标为，与轴的一个交点位于0和1之间，则以下结论：①；②；③若抛物线经过点，则；④若关于的一元二次方程无实数根，则．其中正确结论是      （请填写序号）．

三、解答题（本大题共7小题，共90分．解答应写出文字说明、证明过程或推演步骤）

19．（1）计算：；

（2）解不等式组：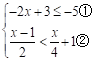

20．2024年中国龙舟公开赛（四川·德阳站），在德阳旌湖沱江桥水域举行，预计来自全国各地1000余名选手将参赛．旌湖两岸高颜值的绿色生态景观绿化带“德阳之窗”将迎接德阳市民以及来自全国各地的朋友近距离的观看比赛．比赛设置男子组、女子组、本地组三个组别，其中男子组将进行A：100米直道竞速赛，B：200米直道竟速赛，C：500米直道竞速赛，D：3000米绕标赛．为了了解德阳市民对于这四个比赛项目的关注程度，随机对部分市民进行了问卷调查（参与问卷调查的每位市民只能选择其中一个项目），将调查得到的数据绘制成数据统计表和扇形统计图（表、图都未完全制作完成）：

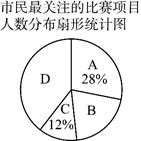
(1)直接写出a、b的值和D所在扇形圆心角的度数；

(2)若当天观看比赛的市民有10000人，试估计当天观看比赛的市民中关注哪个比赛项目的人数最多？大约有多少人？

(3)为了缓解比赛当天城市交通压力，维护交通秩序，德阳交警旌阳支队派出4名交警（2男2女）对该路段进行值守，若在4名交警中任意抽取2名交警安排在同一路口执勤，请用列举法（画树状图或列表）求出恰好抽到的两名交警性别相同的概率．

21．如图，一次函数与反比例函数的图象交于点．

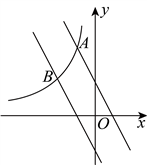
(1)求的值和反比例函数的解析式；

(2)将直线向下平移个单位长度后得直线，若直线与反比例函数的图象的交点为，求的值，并结合图象求不等式的解集．

22．如图，在菱形中，，对角线与相交于点，点为的中点，连接与相交于点，连接并延长交于点．

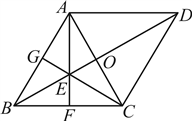
(1)证明：；

(2)证明：．

23．罗江糯米咸鹅蛋是德阳市非物质文化遗产之一，至今有200多年历史，采用罗江当地林下养殖的鹅产的散养鹅蛋，经过传统秘方加以糯米、青豆等食材以16道工序手工制作而成．为了迎接端午节，进一步提升糯米咸鹅蛋的销量，德阳某超市将购进的糯米咸鹅蛋和肉粽进行组合销售，有A、B两种组合方式，其中A组合有4枚糯米咸鹅蛋和6个肉粽，B组合有6枚糯米咸鹅蛋和10个肉粽．A、B两种组合的进价和售价如下表：

(1)求每枚糯米咸鹅蛋和每个肉粽的进价分别为多少？

(2)根据市场需求，超市准备的B种组合数量是A种组合数量的3倍少5件，且两种组合的总件数不超过95件，假设准备的两种组合全部售出，为使利润最大，该超市应准备多少件A种组合？最大利润为多少？

24．如图，抛物线与轴交于点和点，与轴交于点．

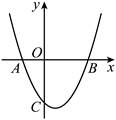
(1)求抛物线的解析式；

(2)当时，求的函数值的取值范围；

(3)将拋物线的顶点向下平移个单位长度得到点，点为抛物线的对称轴上一动点，求的最小值．

25．已知的半径为5，是上两定点，点是上一动点，且的平分线交于点．

(1)证明：点为上一定点；

(2)过点作的平行线交的延长线于点．

①判断与的位置关系，并说明理由；

②若为锐角三角形，求的取值范围

参考答案

1．D

2．B

3．B

5．D

6．C

7．A

8．C

9．C

10．B

11．D

12．C

13．3

14．

15．

16．2

17．1##8

18．①②④

19．（1），（2）

20．(1)，，

(2)D，4000

(3)

21．(1)；反比例函数的解析式为

(2)；不等式的解集为

22．

【详解】（1）证明：∵四边形是菱形，

∴，

∵，

∴是等边三角形，

∵点为的中点，

∴，

∴

∵，

∴．

（2）证明：∵是等边三角形，，，

∴，

∴

∵是等边三角形，

∴，

在和中，

，

∴．

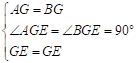23．(1)16， 6

(2)25， 3590

24．(1)

(2)

(3)的最小值为：

25．(1)证明见解析

(2)①与相切，理由见解析；②的取值范围为

【详解】（1）证明：∵的平分线交于点，，

∴，

∴，

∵是上两定点，

∴点为的中点，是一定点；