2024年四川自贡中考数学试卷及答案
第Ⅰ卷 选择题(共48分)
注意事项:必须使用2B铅笔将答案标号填涂在答题卡上对应题目标号的位置上.如需改动,用橡皮擦干净后,再选涂其他答案标号.
一、选择题(共12个小题,每小题4分,共48分.在每题给出的四个选项中,只有一项是符合题目要求的)
1.在0,![]() ,
,![]() ,
,![]() 四个数中,最大的数是( )
四个数中,最大的数是( )
A.![]() B.0 C.
B.0 C.![]() D.
D.![]()
2.据统计,今年“五一”小长假期间,近70000人次游览了自贡中华彩灯大世界.70000用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
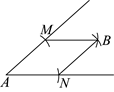
3.如图,以点A为圆心,适当的长为半径画弧,交![]() 两边于点M,N,再分别以M、N为圆心,
两边于点M,N,再分别以M、N为圆心,![]() 的长为半径画弧,两弧交于点B,连接
的长为半径画弧,两弧交于点B,连接![]() .若
.若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列几何体中,俯视图与主视图形状相同的是( )
A.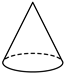 B.
B.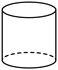 C.
C.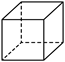 D.
D.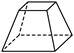
5.学校群文阅读活动中,某学习小组五名同学阅读课外书的本数分别为3,5,7,4,5.这组数据的中位数和众数分别是( )
A.3,4 B.4,4 C.4,5 D.5,5
6.如图,在平面直角坐标系中,![]() ,将
,将![]() 绕点O逆时针旋转
绕点O逆时针旋转![]() 到
到![]() 位置,则点B坐标为( )
位置,则点B坐标为( )
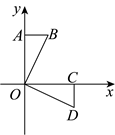
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.我国汉代数学家赵爽在他所著《勾股圆方图注》中,运用弦图(如图所示)巧妙地证明了勾股定理.“赵爽弦图”曾作为2002年第24届国际数学家大会的会徽图案.下列关于“赵爽弦图”说法正确的是( )
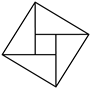
A.是轴对称图形 B.是中心对称图形
C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形也不是中心对称图形
8.关于x的一元二次方程![]() 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
9.一次函数![]() ,二次函数
,二次函数![]() ,反比例函数
,反比例函数![]() 在同一直角坐标系中图象如图所示,则n的取值范围是( )
在同一直角坐标系中图象如图所示,则n的取值范围是( )
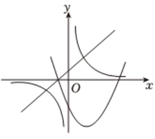
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .A点P从点A出发、以
.A点P从点A出发、以![]() 的速度沿
的速度沿![]() 运动,同时点Q从点C出发,以
运动,同时点Q从点C出发,以![]() 的速度沿
的速度沿![]() 往复运动,当点P到达端点D时,点Q随之停止运动.在此运动过程中,线段
往复运动,当点P到达端点D时,点Q随之停止运动.在此运动过程中,线段![]() 出现的次数是( )
出现的次数是( )
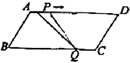
A.3 B.4 C.5 D.6
11.如图,等边![]() 钢架的立柱
钢架的立柱![]() 于点D,
于点D,![]() 长
长![]() .现将钢架立柱缩短成
.现将钢架立柱缩短成![]() ,
,![]() .则新钢架减少用钢( )
.则新钢架减少用钢( )
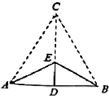
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.如图,在矩形![]() 中,
中,![]() 平分
平分![]() ,将矩形沿直线
,将矩形沿直线![]() 折叠,使点A,B分别落在边
折叠,使点A,B分别落在边![]() 上的点
上的点![]() ,
,![]() 处,
处,![]() ,
,![]() 分别交
分别交![]() 于点G,H.若
于点G,H.若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
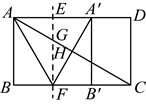
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
第Ⅱ卷(非选择题 共102分)
注意事项:必须使用0.5毫米黑色墨水签字笔在答题卡上题目所指示区域内作答,作图题可先用铅笔绘出,确认后再用0.5毫来黑色墨水签字笔描清楚,答在试题卷上无效.
二、填空题(共6个小题,每小题4分,共24分)
13.分解因式:![]() .
.
14.计算:![]() .
.
15.凸七边形的内角和是 度.
16.一次函数![]() 的值随
的值随![]() 的增大而增大,请写出一个满足条件的
的增大而增大,请写出一个满足条件的![]() 的值 .
的值 .
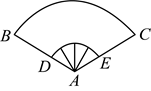
17.龚扇是自贡“小三绝”之一.为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图).扇形外侧两竹条![]() 夹角为
夹角为![]() .
.![]() 长
长![]() ,扇面的
,扇面的![]() 边长为
边长为![]() ,则扇面面积为
,则扇面面积为 ![]() (结果保留
(结果保留![]() )
)
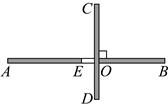
18.九(1)班劳动实践基地内有一块面积足够大的平整空地.地上两段围墙![]() 于点O(如图),其中
于点O(如图),其中![]() 上的
上的![]() 段围墙空缺.同学们测得
段围墙空缺.同学们测得![]() m,
m,![]() m,
m,![]() m,
m,![]() m,
m,![]() m.班长买来可切断的围栏
m.班长买来可切断的围栏![]() m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是
m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是 ![]() .
.
三、解答题(共8个题,共78分)
19.计算:![]()
20.如图,在![]() 中,
中,![]() ,
,![]() .
.
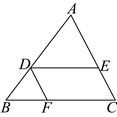
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 平分
平分![]() ,请直接写出
,请直接写出![]() 的形状.
的形状.
21.为传承我国传统节日文化,端午节前夕,某校组织了包粽子活动.已知七(3)班甲组同学平均每小时比乙组多包20个粽子,甲组包150个粽子所用的时间与乙组包120个粽子所用的时间相同.求甲,乙两组同学平均每小时各包多少个粽子.
22.在![]() 中,
中,![]() ,
,![]() 是
是![]() 的内切圆,切点分别为D,E,F.
的内切圆,切点分别为D,E,F.
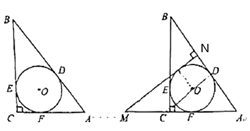
图1 图2
(1)图1中三组相等的线段分别是![]() ,
,![]() ________,
________,![]() ________;若
________;若![]() ,
,![]() ,则
,则![]() 半径长为________;
半径长为________;
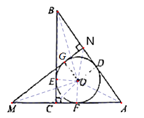
(2)如图2,延长![]() 到点M,使
到点M,使![]() ,过点M作
,过点M作![]() 于点N.
于点N.
求证:![]() 是
是![]() 的切线.
的切线.
23.某校为了解学生身体健康状况,从全校600名学生的体质健康测试结果登记表中,随机选取了部分学生的测试数据进行初步整理(如图1).并绘制出不完整的条形统计图(如图2).
成绩 | 频数 | 百分比 |
不及格 | 3 | a |
及格 | b |
|
良好 | 45 | c |
优秀 | 32 |
|
图1 学生体质健康统计表
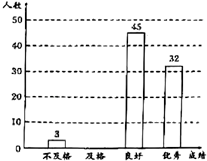
图2 学生体质健康条形图
(1)图1中![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)请补全图2的条形统计图,并估计该校学生体质健康测试结果为“良好”和“优秀”的总人数;
(3)为听取测试建议,学校选出了3名“良好”1名“优秀”学生,再从这4名学生中随机抽取2人参加学校体质健康测试交流会.请用列表或画树状图的方法,计算所抽取的两人均为“良好”的概率
24.如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
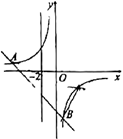
(1)求反比例函数和一次函数的解析式;
(2)P是直线![]() 上的一个动点,
上的一个动点,![]() 的面积为21,求点P坐标;
的面积为21,求点P坐标;
(3)点Q在反比例函数![]() 位于第四象限的图象上,
位于第四象限的图象上,![]() 的面积为21,请直接写出Q点坐标.
的面积为21,请直接写出Q点坐标.
25.为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
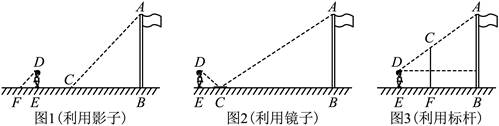
(1)如图1,小张在测量时发现,自己在操场上的影长![]() 恰好等于自己的身高
恰好等于自己的身高![]() .此时,小组同学测得旗杆
.此时,小组同学测得旗杆![]() 的影长
的影长![]() 为
为![]() ,据此可得旗杆高度为________m;
,据此可得旗杆高度为________m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度![]() ,小李到镜面距离
,小李到镜面距离![]() ,镜面到旗杆的距离
,镜面到旗杆的距离![]() .求旗杆高度;
.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
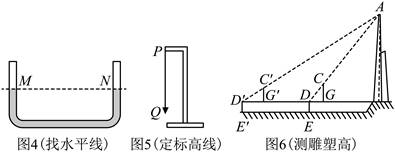
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线![]() 始终垂直于水平地面.
始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线![]() 与标高线交点C,测得标高
与标高线交点C,测得标高![]() ,
,![]() .将观测点D后移
.将观测点D后移![]() 到
到![]() 处,采用同样方法,测得
处,采用同样方法,测得![]() ,
,![]() .求雕塑高度(结果精确到
.求雕塑高度(结果精确到![]() ).
).
26.如图,抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,顶点为P.
两点,顶点为P.
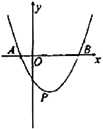
(1)求抛物线的解析式及P点坐标;
(2)抛物线交y轴于点C,经过点A,B,C的圆与y轴的另一个交点为D,求线段![]() 的长;
的长;
(3)过点P的直线![]() 分别与抛物线、直线
分别与抛物线、直线![]() 交于x轴下方的点M,N,直线
交于x轴下方的点M,N,直线![]() 交抛物线对称轴于点E,点P关于E的对称点为Q,
交抛物线对称轴于点E,点P关于E的对称点为Q,![]() 轴于点H.请判断点H与直线
轴于点H.请判断点H与直线![]() 的位置关系,并证明你的结论
的位置关系,并证明你的结论
参考答案
1.C
2.B
3.A
4.C
5.D
6.A
7.B
8.A
9.C
10.B
11.D
12.A
13.![]()
14.1
15.900
16.![]() (答案不唯一)
(答案不唯一)
17.![]()
18.![]()
19.![]()
20.
(1)证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)
![]() 是等腰直角三角形
是等腰直角三角形
21.甲组平均每小时包100个粽子,乙组平均每小时包80个粽子.
22.
(1)![]() ;
;![]() ;1
;1
(2)
证明:连接![]() ,
,![]() ,
,![]() ,作
,作![]() 于点
于点![]() ,
,
设![]() 半径为
半径为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() 是
是![]() 的内切圆,切点分别为D,E,F,
的内切圆,切点分别为D,E,F,
∴![]() ,
,
∴![]() ,
,
同理![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是
是![]() 的切线.
的切线.
23.
(1)![]() ;20;
;20;![]()
(2)补全图见解析,估计该校学生体质健康测试结果为“良好”和“优秀”的总人数为462人;
解:补全条形统计图,如图:
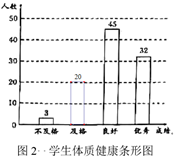
![]() (人),
(人),
估计该校学生体质健康测试结果为“良好”和“优秀”的总人数为462人;
(3)选取的2名学生均为“良好”的概率为![]()
24.(1)![]() ,
,![]()
(2)点P坐标为![]() 或
或![]() ;
;
(3)Q点坐标为![]()
25.(1)![]()
(2)旗杆高度为![]() ;
;
(3)雕塑高度为![]() .
.
26.
(1)![]() ,
,![]()
(2)4
(3)点H在直线![]() 上
上
