2023年山东东营中考数学试题及答案
第Ⅰ卷(选择题 共30分)
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分,选错、不选或选出的答案超过一个均记零分。
1.-2的相反数是( )
A.-2 B.2 C.![]() D.
D.![]()
2.下列运算结果正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.如图,![]() ,点E在线段BC上(不与点B,C重合),连接DE。若
,点E在线段BC上(不与点B,C重合),连接DE。若![]() ,
,![]() ,则∠B=( )
,则∠B=( )
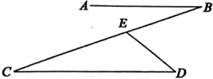
A.10° B.20° C.40° D.60°
4.剪纸是中国最古老的民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录。小文购买了以“剪纸图案”为主题的5张书签,他想送给好朋友小乐一张。小文将书签背面朝上(背面完全相同),让小乐从中随机抽取一张,则小乐抽到的书签图案既是轴对称图形又是中心对称图形的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.为扎实推进“五育”并举工作,加强劳动教育,东营市某中学针对七年级学生开设了“跟我学面点”烹饪课程。课程开设后学校花费6000元购进第一批面粉,用完后学校又花费9600元购进了第二批面粉,第二批面粉的采购量是第一批采购量的1.5倍,但每千克面粉价格提高了0.4元。设第一批面粉采购量为x千克,依题意所列方程正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如果圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面半径是( )
A.3 B.4 C.5 D.6
7.如图,△ABC为等边三角形,点D,E分别在边BC,AB上![]() 。若
。若![]() ,
,![]() ,则AD的长为( )
,则AD的长为( )
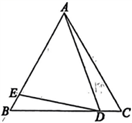
A.1.8 B.2.4 C.3 D.3.2
8.如图,在平面直角坐标系中,菱形OABC的边长为![]() ,点B在x轴的正半轴上,且
,点B在x轴的正半轴上,且![]() ,将菱形OABC绕原点O逆时针方向旋转60°,得到四边形OA'B'C'(点A'与点C重合),则点B'的坐标是( )
,将菱形OABC绕原点O逆时针方向旋转60°,得到四边形OA'B'C'(点A'与点C重合),则点B'的坐标是( )
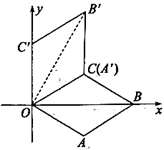
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图,抛物线![]() 与x轴交于点A,B,与y轴交于点C,对称轴为直线
与x轴交于点A,B,与y轴交于点C,对称轴为直线![]() 。若点A的坐标为
。若点A的坐标为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
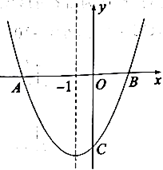
A.![]()
B.![]()
C.![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的一个根
的一个根
D.点![]() ,
,![]() 在抛物线上,当
在抛物线上,当![]() 时
时![]()
10.如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且![]() ,AE平分∠CAD,连接DF,分别交AE,AC于点G,M。P是线段AG上的一个动点,过点P作
,AE平分∠CAD,连接DF,分别交AE,AC于点G,M。P是线段AG上的一个动点,过点P作![]() 垂足为N,连接PM。有下列四个结论:①AE垂直平分DM,②
垂足为N,连接PM。有下列四个结论:①AE垂直平分DM,②![]() 的最小值为
的最小值为![]() ,③
,③![]() ,④
,④![]() 。其中正确的是( )
。其中正确的是( )
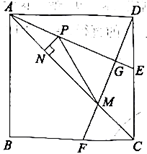
A.①② B.②③④ C.①③④ D.①③
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共8.小题,其中11-14题每小题3分,15-18题每小题4分,共28分。只要求填写最后结果。
11.我国古代数学家祖冲之推算出π.的近似值为![]() ,它与π的误差小于0.0000003。0.000003用科学记数法表示为 。
,它与π的误差小于0.0000003。0.000003用科学记数法表示为 。
12.因式分解:![]() 。
。
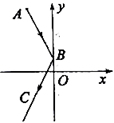
13.如图,一束光线从点![]() 出发,经过y轴上的点
出发,经过y轴上的点![]() 反射后经过点
反射后经过点![]() ,则
,则![]() 的值是 。
的值是 。
14.为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测试成绩的平均数![]() (单位:环)及方差
(单位:环)及方差![]() (单位:环2)如下表所示:
(单位:环2)如下表所示:
| 甲 | 乙 | 丙 | 丁 |
| 9.6 | 8.9 | 9.6 | 9.6 |
| 1.4 | 0.8 | 2.3 | 0.8 |
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择 。
15.一艘船由A港沿北偏东60°方向航行30km至B港,然后再沿北偏西30°方向航行40km至C港,则A,C两港之间的距离为 km。
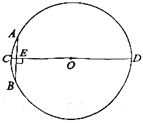
16.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小。以锯锯之,深一寸,锯道长一尺。问:径几何?”转化为现在的数学语言表达就是:如图,CD为⊙O的直径,弦![]() ,垂足为E,
,垂足为E,![]() 寸,
寸,![]() 寸,则直径CD的长度为 寸。
寸,则直径CD的长度为 寸。
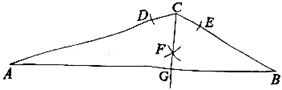
17.如图,在△ABC中,以点C为圆心,任意长为半径作弧,分别交AC,BC于点D,E;分别以点D,E为圆心,大于![]() 的长为半径作弧,两弧交于点F;作射线CF交AB于点G。若
的长为半径作弧,两弧交于点F;作射线CF交AB于点G。若![]() ,
,![]() ,△BCG的面积为8,则△ACG的面积为 。
,△BCG的面积为8,则△ACG的面积为 。
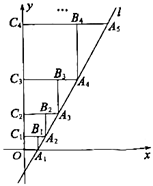
18.如图,在平面直角坐标系中,直线l:![]() 与x轴交于点
与x轴交于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() 点
点![]() 在y轴上,延长
在y轴上,延长![]() 交直线l于点
交直线l于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 在y轴上,以同样的方式依次作正方形
在y轴上,以同样的方式依次作正方形![]() ,…,正方形
,…,正方形![]() ,则点
,则点![]() 的横坐标是 。
的横坐标是 。
三、解答题:本大题共7小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
19.(本题满分8分,第(1)题4分,第(2)题4分)
(1)计算:![]() ;
;
(2)先化简,再求值:![]() ,化简后,从
,化简后,从![]() 的范围内选择一个你喜欢的整数作为x的值代入求值。
的范围内选择一个你喜欢的整数作为x的值代入求值。
20.(本题满分8分)
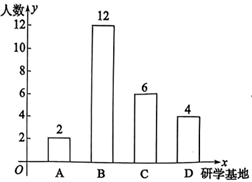
随着新课程标准的颁布,为落实立德树人根本任务,东营市各学校组织了丰富多彩的研学活动,得到家长、社会的一致好评。某中学为进一步提高研学质量,着力培养学生的核心素养,选取了A.“青少年科技馆”,B.“黄河入海口湿地公园”,C.“孙子文化园”,D.“白鹭湖营地”四个研学基地进行研学。为了解学生对以上研学基地的喜欢情况,随机抽取部分学生进行调查统计(每名学生只能选择一个研学基地),并将调查结果绘制成了两幅不完整的统计图(如图所示).
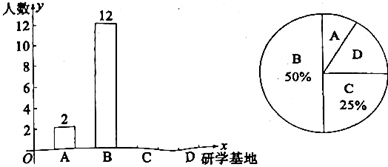
请根据统计图中的信息解答下列问题:
(1)在本次调查中,一共抽取了 名学生,在扇形统计图中A所对应圆心角的度数为 ;
(2)将上面的条形统计图补充完整;
(3)若该校共有480名学生,请你估计选择研学基地C的学生人数;
(4)学校想从选择研学基地D的学生中选取两名学生了解他们对研学活动的看法,已知选择研学基地D的学生中恰有两名女生,请用列表法或画树状图的方法求出所选2人都是男生的概率。
21.(本题满分8分)
如图,在△ABC中,![]() ,以AB为直径的⊙O交BC于点D,
,以AB为直径的⊙O交BC于点D,![]() ,垂足为E。
,垂足为E。
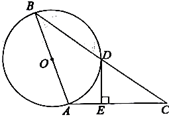
(1)求证:DE是⊙O的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长。
的长。
22.(本题满分8分)
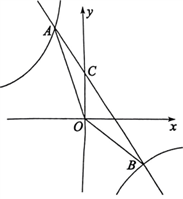
如图,在平面直角坐标系中,一次函数![]() 与反比例函数
与反比例函数![]() 交于
交于![]() ,
,![]() 两点,与y轴交于点C,连接OA,OB。
两点,与y轴交于点C,连接OA,OB。
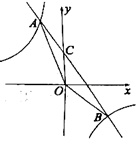
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)请根据图象直接写出不等式![]() 的解集。
的解集。
23.(本题满分8分)
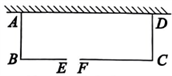
如图,老李想用长为70m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD,并在边BC上留一个2m宽的门(建在EF处,另用其他材料)。
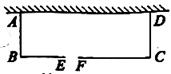
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为640![]() 的羊圈?
的羊圈?
(2)羊圈的面积能达到650![]() 吗?如果能,请你给出设计方案;如果不能,请说明理由。
吗?如果能,请你给出设计方案;如果不能,请说明理由。
24.(本题满分10分)
(1)用数学的眼光观察
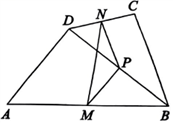
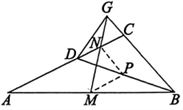
如图①,在四边形ABCD中,![]() ,P是对角线BD的中点,M是AB的中点,N是DC的中点。求证:
,P是对角线BD的中点,M是AB的中点,N是DC的中点。求证:![]() 。
。
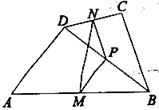
(2)用数学的思维思考
如图②,延长图①中的线段AD交MN的延长线于点E,延长线段BC交MN的延长线于点F。求证:![]() 。
。
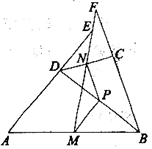
(3)用数学的语言表达
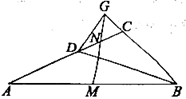
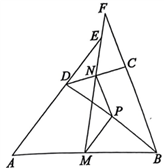
如图③,在△ABC中,![]() ,点D在AC上,
,点D在AC上,![]() ,M是AB的中点,N是DC的中点,连接MN并延长,与BC的延长线交于点G,连接GD。若
,M是AB的中点,N是DC的中点,连接MN并延长,与BC的延长线交于点G,连接GD。若![]() ,试判断△CGD的形状,并进行证明。
,试判断△CGD的形状,并进行证明。
25.(本题满分12分)
如图,抛物线过点![]() ,
,![]() ,矩形ABCD的边AB在线段OE上(点B在点A的左侧),点C,D在抛物线上。设
,矩形ABCD的边AB在线段OE上(点B在点A的左侧),点C,D在抛物线上。设![]() ,当
,当![]() 时,
时,![]() 。
。
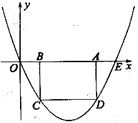
(1)求抛物线的函数表达式;
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持![]() 时的矩形ABCD不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形ABCD的面积时,求抛物线平移的距离。
时的矩形ABCD不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形ABCD的面积时,求抛物线平移的距离。
参考答案
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得3分,共30分。选错、不选或选出的答案超过一个均记零分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | D | B | C | A | A | C | B | C | D |
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分。只要求填写最后结果。
11.![]() ;12.
;12.![]() ;13.-1;14.丁;15.50;16.26;17.12;18.
;13.-1;14.丁;15.50;16.26;17.12;18.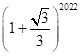
三、解答题:本大题共7小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
19.(本题满分8分,第(1)题4分,第(2)题4分)
解:(1)原式![]()
![]() ;
;
(2)原式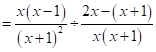
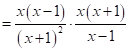
![]() 。
。
由题意可知![]() ,
,![]() ,
,![]() ,
,
∴当![]() 时,原式
时,原式![]() 。
。
20.(本题满分8分)
(1)24,30°;
(2)如图所示:
(3)![]() (名);
(名);
答:该校选择研学基地C的学生人数是120名。
(4)选择研学基地D的学生有2名男生和2名女生,画树状图如下:
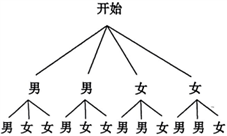
共有12种等可能的结果,其中所选2人都是男生的结果有2种,
∴P(所选2人都是男生)![]() 。
。
21.(本题满分8分)
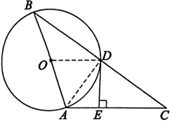
(1)证明:连接OD。
∵![]() ,
,
∴![]() 。
。
∵![]() ,
,
∴![]() 。
。
∴![]() 。
。
∴![]() 。
。
∴![]() 。
。
∵![]() ,
,
∴![]() 。
。
∴![]() 。
。
∵OD是⊙O的半径,
∴DE是⊙O的切线。
(2)解:连接AD。
∵AB是⊙O的直径,
∴![]() 。
。
在Rt△ADC中,![]() ,
,![]() ,
,
∴![]() 。
。
∴![]() 。
。
∴![]() 。
。
∵![]() ,
,
∴![]() 。
。
∴![]() 。
。
∴![]() 。
。
22.(本题满分8分)
解:
(1)∵点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,
解得![]() 。
。
∴反比例函数的表达式为![]() 。
。
∵![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,
解得![]() ,
,![]() (舍去)。
(舍去)。
∴点A的坐标为![]() 。
。
∵点A,B在一次函数![]() 的图象上,
的图象上,
把点![]() ,
,![]() 分别代入,得
分别代入,得![]() ,
,
解得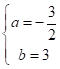 ,
,
∴一次函数的表达式为![]() 。
。
(2)∵点C为直线AB与y轴的交点,
∴![]() ,
,
∴![]()
![]()
![]()
![]() 。
。
(3)![]() 或
或![]() 。
。
23.(本题满分8分)
解:
(1)设矩形ABCD的边![]() ,则边
,则边![]() m。
m。
根据题意,得![]() 。
。
化简,得![]() 。
。
解得![]() ,
,![]() 。
。
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 。
。
答:当羊圈的长为40m,宽为16m或长为32m,宽为20m时,能围成一个面积为640![]() 的羊圈。
的羊圈。
(2)答:不能。
理由:由题意,得![]() 。
。
化简,得![]() 。
。
∵![]() ,
,
∴一元二次方程没有实数根。
∴羊圈的面积不能达到650![]() 。
。
24.(本题满分10分)
(1)证明:
∵P是BD的中点,M是AB的中点,
∴![]() 。
。
同理,![]() 。
。
∵![]() ,
,
∴![]() 。
。
∴![]() 。
。
(2)证明:∵P是BD的中点,N是DC的中点,
∴![]() 。
。
∴![]() 。
。
同理,![]() 。
。
∵![]() ,
,
∴![]() 。
。
(3)△CGD是直角三角形。
证明:如图,取BD的中点P,连接PM,PN。
∵M是AB的中点,
∴![]() ,
,![]() 。
。
同理,![]() ,
,![]() 。
。
∵![]() ,
,
∴![]() 。
。
∴![]() 。
。
∵![]() ,
,
∴![]() 。
。
∴![]() 。
。
∵![]() ,
,
∴![]() 。
。
又∵![]() ,
,
∴△CGN是等边三角形。
∴![]() 。
。
又∵![]() ,
,
∴![]() 。
。
∴![]() 。
。
∴![]() 。
。
∴△CGD是直角三角形。.
25.(本题满分12分)
解:
(1)设抛物线的函数表达式为![]() 。
。
∵当![]() 时,
时,![]() ,
,
∴点C的坐标为![]() 。
。
将点C坐标代入表达式,得![]() ,
,
解得![]() 。
。
∴抛物线的函数表达式为![]() 。
。
(2)由抛物线的对称性得![]() ,
,
∴![]() 。
。
当![]() 时,
时,![]() 。
。
∴矩形ABCD的周长为
![]()
![]()
![]() 。
。
∵![]() ,
,
∴当![]() 时,矩形ABCD的周长有最大值,最大值为
时,矩形ABCD的周长有最大值,最大值为![]() 。
。
(3)连接AC,BD相交于点P,连接OC,取OC的中点Q,连接PQ。
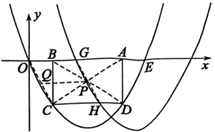
∵直线GH平分矩形ABCD,
∴直线GH过点P。.由平移的性质可知,四边形OCHG是平行四边形,
∴![]() 。
。
∵四边形ABCD是矩形,
∴P是AC的中点。
∴![]() 。
。
当![]() 时,点A的坐标为
时,点A的坐标为![]() ,
,
∴![]() 。
。
∴抛物线平移的距离是4。
