2023年河北中考数学试题及答案
一、选择题
1. 代数式![]() 的意义可以是( )
的意义可以是( )
A. ![]() 与x的和 B.
与x的和 B. ![]() 与x的差 C.
与x的差 C. ![]() 与x的积 D.
与x的积 D. ![]() 与x的商
与x的商
2. 淇淇一家要到革命圣地西柏坡参观.如图,西柏坡位于淇淇家南偏西![]() 的方向,则淇淇家位于西柏坡的( )
的方向,则淇淇家位于西柏坡的( )
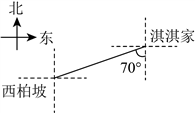
A. 南偏西![]() 方向 B. 南偏东
方向 B. 南偏东![]() 方向
方向
C. 北偏西![]() 方向 D. 北偏东
方向 D. 北偏东![]() 方向
方向
3. 化简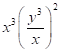 的结果是( )
的结果是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 1有7张扑克牌如图所示,将其打乱顺序后,背面朝上放在桌面上.若从中随机抽取一张,则抽到的花色可能性最大的是( )

A. ![]() B.
B. ![]() C.
C.  D.
D. ![]()
5. 四边形![]() 的边长如图所示,对角线
的边长如图所示,对角线![]() 的长度随四边形形状的改变而变化.当
的长度随四边形形状的改变而变化.当![]() 为等腰三角形时,对角线
为等腰三角形时,对角线![]() 的长为( )
的长为( )
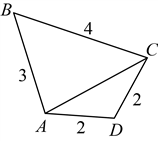
A 2 B. 3 C. 4 D. 5
6. 若k为任意整数,则![]() 的值总能( )
的值总能( )
A. 被2整除 B. 被3整除 C. 被5整除 D. 被7整除
7. 若![]() ,则
,则![]() ( )
( )
A. 2 B. 4 C. ![]() D.
D. ![]()
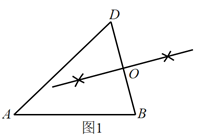
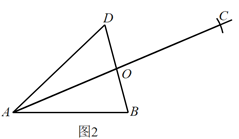
8. 综合实践课上,嘉嘉画出![]() ,利用尺规作图找一点C,使得四边形
,利用尺规作图找一点C,使得四边形![]() 为平行四边形.图1~图3是其作图过程.
为平行四边形.图1~图3是其作图过程.
(1)作
| (2)连接
| (3)连接
|
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A. 两组对边分别平行 B. 两组对边分别相等
C. 对角线互相平分 D. 一组对边平行且相等
9. 如图,点![]() 是
是![]() 的八等分点.若
的八等分点.若![]() ,四边形
,四边形![]() 的周长分别为a,b,则下列正确的是( )
的周长分别为a,b,则下列正确的是( )
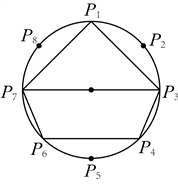
A. ![]() B.
B. ![]() C.
C. ![]() D. a,b大小无法比较
D. a,b大小无法比较
10. 光年是天文学上的一种距离单位,一光年是指光在一年内走过的路程,约等于![]() .下列正确的是( )
.下列正确的是( )
A. ![]() B.
B. ![]()
C. ![]() 是一个12位数 D.
是一个12位数 D. ![]() 是一个13位数
是一个13位数
11. 如图,在![]() 中,
中,![]() ,点M是斜边
,点M是斜边![]() 的中点,以
的中点,以![]() 为边作正方形
为边作正方形![]() ,若
,若![]() ,则
,则![]() ( )
( )
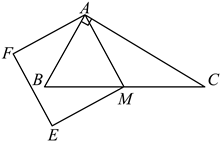
A. ![]() B.
B. ![]() C. 12 D. 16
C. 12 D. 16
12. 如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至还需再放这样的正方体( )
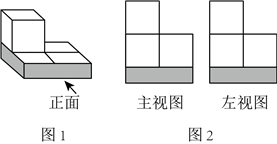
A. 1个 B. 2个 C. 3个 D. 4个
13. 在![]() 和
和![]() 中,
中,![]() .已知
.已知![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
14. 如图是一种轨道示意图,其中![]() 和
和![]() 均为半圆,点M,A,C,N依次在同一直线上,且
均为半圆,点M,A,C,N依次在同一直线上,且![]() .现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为
.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为![]() 和
和![]() .若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是( )
.若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是( )
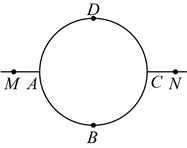
A. 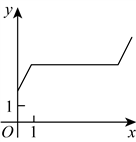 B.
B. 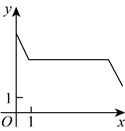
C. 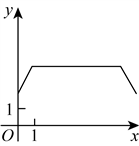 D.
D. 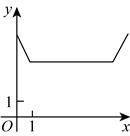
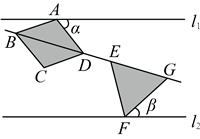
15. 如图,直线![]() ,菱形
,菱形![]() 和等边
和等边![]() 在
在![]() ,
,![]() 之间,点A,F分别在
之间,点A,F分别在![]() ,
,![]() 上,点B,D,E,G在同一直线上:若
上,点B,D,E,G在同一直线上:若![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
16. 已知二次函数![]() 和
和![]() (m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )
(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )
A. 2 B. ![]() C. 4 D.
C. 4 D. ![]()
二、填空题
17. 如图,已知点![]() ,反比例函数
,反比例函数![]() 图像的一支与线段
图像的一支与线段![]() 有交点,写出一个符合条件的k的数值:_________.
有交点,写出一个符合条件的k的数值:_________.

18. 根据下表中的数据,写出a的值为_______.b的值为_______.
x 结果 代数式 | 2 | n |
| 7 | b |
| a | 1 |
19. 将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上,两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图2中
(1)![]() ______度.
______度.
(2)中间正六边形的中心到直线l的距离为______(结果保留根号).

三、解答题
20. 某磁性飞镖游戏的靶盘如图.珍珍玩了两局,每局投10次飞镖,若投到边界则不计入次数,需重新投,计分规则如下:
投中位置 | A区 | B区 | 脱靶 |
一次计分(分) | 3 | 1 |
|
在第一局中,珍珍投中A区4次,B区2次,脱靶4次.
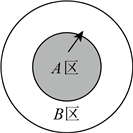
(1)求珍珍第一局的得分;
(2)第二局,珍珍投中A区k次,B区3次,其余全部脱靶.若本局得分比第一局提高了13分,求k的值.
21. 现有甲、乙、丙三种矩形卡片各若干张,卡片的边长如图1所示![]() .某同学分别用6张卡片拼出了两个矩形(不重叠无缝隙),如图2和图3,其面积分别为
.某同学分别用6张卡片拼出了两个矩形(不重叠无缝隙),如图2和图3,其面积分别为![]() .
.
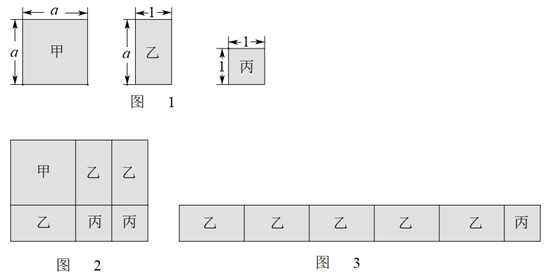
(1)请用含a的式子分别表示![]() ;当
;当![]() 时,求
时,求![]() 的值;
的值;
(2)比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
22. 某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,调意度从低到高为1分,2分,3分,4分,5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中随机抽取了20份,下图是根据这20份问卷中的客户所评分数绘制的统计图.

(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改;
(2)监督人员从余下的问卷中又随机抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于![]() 分,求监督人员抽取的问卷所评分数为几分?与(1)相比,中位数是否发生变化?
分,求监督人员抽取的问卷所评分数为几分?与(1)相比,中位数是否发生变化?
23. 嘉嘉和淇淇![]() 玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点![]() 处将沙包(看成点)抛出,并运动路线为抛物线
处将沙包(看成点)抛出,并运动路线为抛物线![]() 的一部分,淇淇恰在点
的一部分,淇淇恰在点![]() 处接住,然后跳起将沙包回传,其运动路线为抛物线
处接住,然后跳起将沙包回传,其运动路线为抛物线![]() 的一部分.
的一部分.
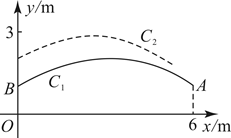
(1)写出![]() 的最高点坐标,并求a,c的值;
的最高点坐标,并求a,c的值;
(2)若嘉嘉在x轴上方![]() 的高度上,且到点A水平距离不超过
的高度上,且到点A水平距离不超过![]() 的范围内可以接到沙包,求符合条件的n的整数值.
的范围内可以接到沙包,求符合条件的n的整数值.
24. 装有水的水槽放置在水平台面上,其横截面是以![]() 为直径的半圆
为直径的半圆![]() ,
,![]() ,如图1和图2所示,
,如图1和图2所示,![]() 为水面截线,
为水面截线,![]() 为台面截线,
为台面截线,![]() .
.
计算:在图1中,已知![]() ,作
,作![]() 于点
于点![]() .
.
(1)求![]() 的长.
的长.
操作:将图1中的水面沿![]() 向右作无滑动的滚动,使水流出一部分,当
向右作无滑动的滚动,使水流出一部分,当![]() 时停止滚动,如图2.其中,半圆的中点为
时停止滚动,如图2.其中,半圆的中点为![]() ,
,![]() 与半圆的切点为
与半圆的切点为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]()
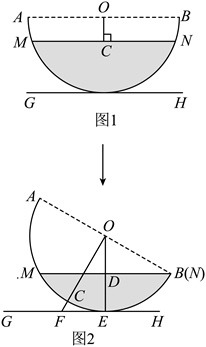
探究:在图2中
(2)操作后水面高度下降了多少?
(3)连接OQ并延长交GH于点F,求线段![]() 与
与![]() 的长度,并比较大小.
的长度,并比较大小.
25. 在平面直角坐标系中,设计了点的两种移动方式:从点![]() 移动到点
移动到点![]() 称为一次甲方式:从点
称为一次甲方式:从点![]() 移动到点
移动到点![]() 称为一次乙方式.
称为一次乙方式.
例、点P从原点O出发连续移动2次;若都按甲方式,最终移动到点![]() ;若都按乙方式,最终移动到点
;若都按乙方式,最终移动到点![]() ;若按1次甲方式和1次乙方式,最终移动到点
;若按1次甲方式和1次乙方式,最终移动到点![]() .
.
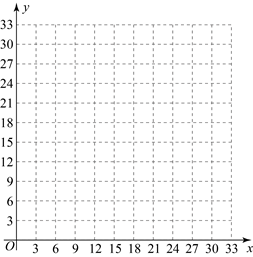
(1)设直线![]() 经过上例中的点
经过上例中的点![]() ,求
,求![]() 的解析式;并直接写出将
的解析式;并直接写出将![]() 向上平移9个单位长度得到的直线
向上平移9个单位长度得到的直线![]() 的解析式;
的解析式;
(2)点P从原点O出发连续移动10次,每次移动按甲方式或乙方式,最终移动到点![]() .其中,按甲方式移动了m次.
.其中,按甲方式移动了m次.
①用含m的式子分别表示![]() ;
;
②请说明:无论m怎样变化,点Q都在一条确定的直线上.设这条直线为![]() ,在图中直接画出
,在图中直接画出![]() 的图象;
的图象;
(3)在(1)和(2)中的直线![]() 上分别有一个动点
上分别有一个动点![]() ,横坐标依次为
,横坐标依次为![]() ,若A,B,C三点始终在一条直线上,直接写出此时a,b,c之间的关系式.
,若A,B,C三点始终在一条直线上,直接写出此时a,b,c之间的关系式.
26. 如图1和图2,平面上,四边形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() .将线段
.将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的平分线
的平分线![]() 所在直线交折线
所在直线交折线![]() 于点
于点![]() ,设点
,设点![]() 在该折线上运动的路径长为
在该折线上运动的路径长为![]() ,连接
,连接![]() .
.

(1)若点![]() 在
在![]() 上,求证:
上,求证:![]() ;
;
(2)如图2.连接![]() .
.
①求![]() 的度数,并直接写出当
的度数,并直接写出当![]() 时,
时,![]() 的值;
的值;
②若点![]() 到
到![]() 的距离为
的距离为![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,请直接写出点
时,请直接写出点![]() 到直线
到直线![]() 的距离.(用含
的距离.(用含![]() 的式子表示)
的式子表示)
参考答案
一、选择题
【1题答案】
【答案】C
【2题答案】
【答案】D
【3题答案】
【答案】A
【4题答案】
【答案】B
【5题答案】
【答案】B
【6题答案】
【答案】B
【7题答案】
【答案】A
【8题答案】
【答案】C
【9题答案】
【答案】A
【10题答案】
【答案】D
【11题答案】
【答案】B
【12题答案】
【答案】B
【13题答案】
【答案】C
【14题答案】
【答案】D
【15题答案】
【答案】C
【16题答案】
【答案】A
二、填空题
【17题答案】
【答案】4(答案不唯一,满足![]() 均可)
均可)
【18题答案】
【答案】 ①. ![]() ②.
②. ![]()
【19题答案】
【答案】 ①. ![]() ②.
②. ![]()
三、解答题
【20题答案】
【答案】(1)珍珍第一局的得分为6分;
(2)![]() .
.
【21题答案】
【答案】(1)![]() ,
,![]() ,当
,当![]() 时,
时,![]()
(2)![]() ,理由见解析
,理由见解析
【22题答案】
【答案】(1)中位数为![]() 分,平均数为
分,平均数为![]() 分,不需要整改
分,不需要整改
(2)监督人员抽取的问卷所评分数为5分,中位数发生了变化,由![]() 分变成4分
分变成4分
【23题答案】
【答案】(1)![]() 的最高点坐标为
的最高点坐标为![]() ,
,![]() ,
,![]() ;
;
(2)符合条件的n的整数值为4和5.
【24题答案】
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() .
.
【25题答案】
【答案】(1)![]() 的解析式为
的解析式为![]() ;
;![]() 的解析式为
的解析式为![]() ;
;
(2)①![]() ;②
;②![]() 的解析式为
的解析式为![]() ,图象见解析;
,图象见解析;
(3)![]()
【26题答案】
【答案】(1)见解析 (2)①![]() ,
,![]() ;②
;②![]() 或
或![]()
(3)![]()