2023年天津高考数学试题及答案
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 已知集合![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2. “![]() ”是“
”是“![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分又不必要条件
3. 若![]() ,则
,则![]() 的大小关系为( )
的大小关系为( )
A. ![]() B.
B. ![]()
C![]()
![]() D.
D. ![]()
4. 函数![]() 的图象如下图所示,则
的图象如下图所示,则![]() 的解析式可能为( )
的解析式可能为( )
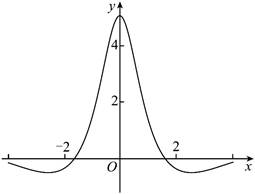
A![]()
![]() B.
B. ![]()
C. ![]() D.
D. ![]()
5. 已知函数![]() 的一条对称轴为直线
的一条对称轴为直线![]() ,一个周期为4,则
,一个周期为4,则![]() 的解析式可能为( )
的解析式可能为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
6. 已知![]() 为等比数列,
为等比数列,![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,则
,则![]() 的值为( )
的值为( )
A. 3 B. 18 C. 54 D. 152
7. 调查某种群花萼长度和花瓣长度,所得数据如图所示,其中相关系数![]() ,下列说法正确的是( )
,下列说法正确的是( )

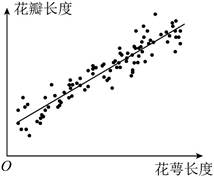
A. 花瓣长度和花萼长度没有相关性
B. 花瓣长度和花萼长度呈现负相关
C. 花瓣长度和花萼长度呈现正相关
D. 若从样本中抽取一部分,则这部分的相关系数一定是![]()
8. 在三棱锥![]() 中,线段
中,线段![]() 上的点
上的点![]() 满足
满足![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,则三棱锥
,则三棱锥![]() 和三棱锥
和三棱锥![]() 的体积之比为( )
的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9. 双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() .过
.过![]() 作其中一条渐近线的垂线,垂足为
作其中一条渐近线的垂线,垂足为![]() .已知
.已知![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则双曲线的方程为( )
,则双曲线的方程为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.
10. 已知![]() 是虚数单位,化简
是虚数单位,化简![]() 的结果为_________.
的结果为_________.
11. 在![]() 的展开式中,
的展开式中,![]() 项的系数为_________.
项的系数为_________.
12. 过原点![]() 一条直线与圆
一条直线与圆![]() 相切,交曲线
相切,交曲线![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的值为_________.
的值为_________.
13. 甲乙丙三个盒子中装有一定数量的黑球和白球,其总数之比为![]() .这三个盒子中黑球占总数的比例分别为
.这三个盒子中黑球占总数的比例分别为![]() .现从三个盒子中各取一个球,取到的三个球都是黑球的概率为_________;将三个盒子混合后任取一个球,是白球的概率为_________.
.现从三个盒子中各取一个球,取到的三个球都是黑球的概率为_________;将三个盒子混合后任取一个球,是白球的概率为_________.
14. 在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,若设
的中点,若设![]() ,则
,则![]() 可用
可用![]() 表示为_________;若
表示为_________;若![]() ,则
,则![]() 的最大值为_________.
的最大值为_________.
15. 若函数![]() 有且仅有两个零点,则
有且仅有两个零点,则![]() 的取值范围为_________.
的取值范围为_________.
三、解答题:本大题共5小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16. 在![]() 中,角
中,角![]() 所对
所对![]() 边分別是
边分別是![]() .已知
.已知![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值;
的值;
(3)求![]() .
.
17. 三棱台![]() 中,若
中,若![]() 面
面![]() ,
,![]() 分别是
分别是![]() 中点.
中点.
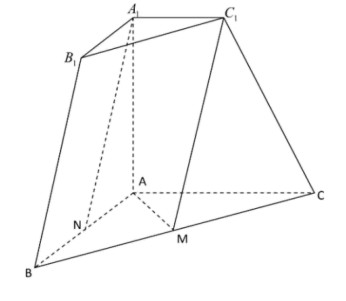
(1)求证:![]() //平面
//平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成夹角
所成夹角![]() 余弦值;
余弦值;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
18. 设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,右焦点为
,右焦点为![]() ,已知
,已知![]() .
.
(1)求椭圆方程及其离心率;
(2)已知点![]() 是椭圆上一动点(不与端点重合),直线
是椭圆上一动点(不与端点重合),直线![]() 交
交![]() 轴于点
轴于点![]() ,若三角形
,若三角形![]() 的面积是三角形
的面积是三角形![]() 面积的二倍,求直线
面积的二倍,求直线![]() 的方程.
的方程.
19. 已知![]() 是等差数列,
是等差数列,![]() .
.
(1)求![]() 的通项公式和
的通项公式和![]() .
.
(2)已知![]() 为等比数列,对于任意
为等比数列,对于任意![]() ,若
,若![]() ,则
,则![]() ,
,
(Ⅰ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅱ)求![]() 的通项公式及其前
的通项公式及其前![]() 项和.
项和.
20. 已知函数![]() .
.
(1)求曲线![]() 在
在![]() 处切线的斜率;
处切线的斜率;
(2)当![]() 时,证明:
时,证明:![]() ;
;
(3)证明:![]() .
.
参考答案
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 【答案】A
2. 【答案】B
3. 【答案】D
4. 【答案】D
5. 【答案】B
6. 【答案】C
7. 【答案】C
8. 【答案】B
9. 【答案】D
二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分
10.【答案】![]()
11.【答案】![]()
12.【答案】![]()
13.【答案】 ①. ![]() ②.
②. ![]()
14.【答案】 ①. ![]() ②.
②. ![]()
15. 【答案】![]()
三、解答题:本大题共5小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16. 在![]() 中,角
中,角![]() 所对的边分別是
所对的边分別是![]() .已知
.已知![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值;
的值;
(3)求![]() .
.
【答案】(1)![]()
(2)![]()
(3)![]()
【小问1详解】
由正弦定理可得,![]() ,即
,即![]() ,解得:
,解得:![]() ;
;
【小问2详解】
由余弦定理可得,![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() (舍去).
(舍去).
【小问3详解】
由正弦定理可得,![]() ,即
,即![]() ,解得:
,解得:![]() ,而
,而![]() ,
,
所以![]() 都为锐角,因此
都为锐角,因此![]() ,
,![]() ,
,
故![]() .
.
17. 三棱台![]() 中,若
中,若![]() 面
面![]() ,
,![]() 分别是
分别是![]() 中点.
中点.
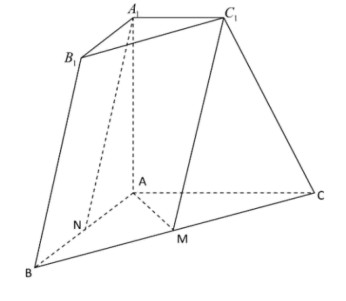
(1)求证:![]() //平面
//平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成夹角的余弦值;
所成夹角的余弦值;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析
(2)![]()
(3)![]()
![]() 小问1详解】
小问1详解】
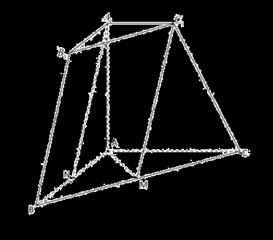
连接![]() .由
.由![]() 分别是
分别是![]() 的中点,根据中位线性质,
的中点,根据中位线性质,![]() //
//![]() ,且
,且![]() ,
,
由棱台性质,![]() //
//![]() ,于是
,于是![]() //
//![]() ,由
,由![]() 可知,四边形
可知,四边形![]() 是平行四边形,则
是平行四边形,则![]() //
//![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,于是
,于是![]() //平面
//平面![]() .
.
【小问2详解】
过![]() 作
作![]() ,垂足为
,垂足为![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
由![]() 面
面![]() ,
,![]() 面
面![]() ,故
,故![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() .
.
由![]() 平面
平面![]() ,故
,故![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() ,于是
,于是![]() 平面
平面![]() ,
,
由![]() 平面
平面![]() ,故
,故![]() .于是平面
.于是平面![]() 与平面
与平面![]() 所成角即
所成角即![]() .
.
又![]() ,
,![]() ,则
,则![]() ,故
,故![]() ,在
,在![]() 中,
中,![]() ,则
,则![]() ,
,
于是![]()
 【小问3详解】
【小问3详解】
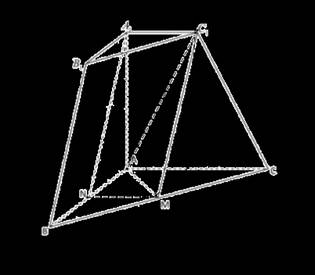
[方法一:几何法]
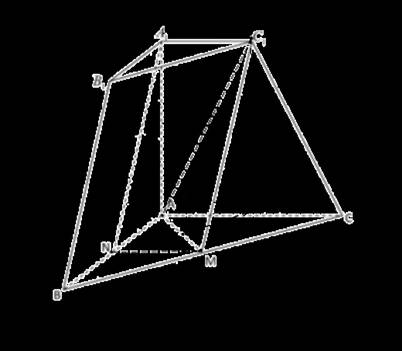
过![]() 作
作![]() ,垂足为
,垂足为![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() .
.
由题干数据可得,![]() ,
,![]() ,根据勾股定理,
,根据勾股定理,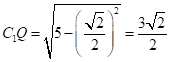 ,
,
由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() ,于是
,于是![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,则
,则![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
在![]() 中,
中,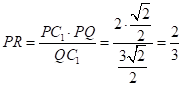 ,
,
又![]() ,故点
,故点![]() 到平面
到平面![]() 的距离是
的距离是![]() 到平面
到平面![]() 的距离的两倍,
的距离的两倍,
即点![]() 到平面
到平面![]() 的距离是
的距离是![]() .
.
[方法二:等体积法]
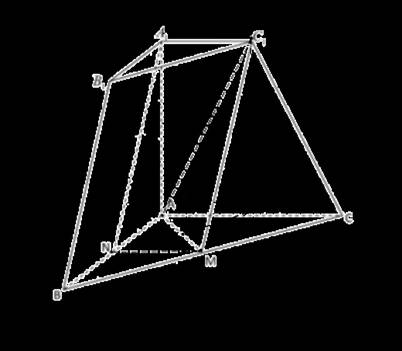
辅助线同方法一.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
![]() ,
,
![]() .
.
由![]() ,即
,即![]() .
.
18. 设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,右焦点为
,右焦点为![]() ,已知
,已知![]() .
.
(1)求椭圆方程及其离心率;
(2)已知点![]() 是椭圆上一动点(不与端点重合),直线
是椭圆上一动点(不与端点重合),直线![]() 交
交![]() 轴于点
轴于点![]() ,若三角形
,若三角形![]() 的面积是三角形
的面积是三角形![]() 面积的二倍,求直线
面积的二倍,求直线![]() 的方程.
的方程.
【答案】(1)椭圆的方程为![]() ,离心率为
,离心率为![]() .
.
(2)![]() .
.
【小问1详解】
如图,
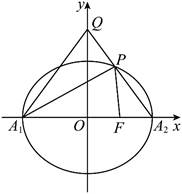
由题意得![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
所以椭圆的方程为![]() ,离心率为
,离心率为![]() .
.
【小问2详解】
由题意得,直线![]() 斜率存在,由椭圆的方程为
斜率存在,由椭圆的方程为![]() 可得
可得![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
联立方程组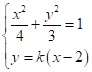 ,消去
,消去![]() 整理得:
整理得:![]() ,
,
由韦达定理得![]() ,所以
,所以![]() ,
,
所以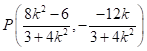 ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,即
,即![]() ,
,
解得![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
19. 已知![]() 是等差数列,
是等差数列,![]() .
.
(1)求![]() 的通项公式和
的通项公式和![]() .
.
(2)已知![]() 为等比数列,对于任意
为等比数列,对于任意![]() ,若
,若![]() ,则
,则![]() ,
,
(Ⅰ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅱ)求![]() 的通项公式及其前
的通项公式及其前![]() 项和.
项和.
【答案】(1)![]() ,
,![]() ;
;
(2)(Ⅰ)证明见解析;(Ⅱ)![]() ,前
,前![]() 项和为
项和为![]() .
.
【小问1详解】
由题意可得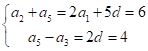 ,解得
,解得![]() ,
,
则数列![]() 的通项公式为
的通项公式为![]() ,
,
注意到![]() ,从
,从![]() 到
到![]() 共有
共有![]() 项,
项,
故![]() .
.
![]() 小问2详解】
小问2详解】
(Ⅰ)由题意可知,当![]() 时,
时,![]() ,
,
取![]() ,则
,则![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
取![]() ,此时
,此时![]() ,
,
据此可得![]() ,
,
综上可得:![]() .
.
(Ⅱ)由(Ⅰ)可知:![]() ,
,
据此猜测![]() ,
,
否则,若数列的公比![]() ,则
,则![]() ,
,
注意到![]() ,则
,则![]() 不恒成立,即
不恒成立,即![]() 不恒成立,
不恒成立,
此时无法保证![]() ,
,
若数列的公比![]() ,则
,则![]() ,
,
注意到![]() ,则
,则![]() 不恒成立,即
不恒成立,即![]() 不恒成立,
不恒成立,
此时无法保证![]() ,
,
综上,数列的公比为![]() ,则数列的通项公式为
,则数列的通项公式为![]() ,
,
其前![]() 项和为:
项和为:![]() .
.
20. 已知函数![]()
(1)求曲线![]() 在
在![]() 处切线的斜率;
处切线的斜率;
(2)当![]() 时,证明:
时,证明:![]() ;
;
(3)证明:![]() .
.
【答案】(1)![]()
(2)证明见解析 (3)证明见解析
【小问1详解】
![]() ,则
,则![]() ,
,
所以![]() ,故
,故![]() 处的切线斜率为
处的切线斜率为![]() ;
;
【小问2详解】
要证![]() 时
时![]() ,即证
,即证![]() ,
,
令![]() 且
且![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上递增,则
上递增,则![]() ,即
,即![]() .
.
所以![]() 时
时![]() .
.
【小问3详解】
设![]() ,
,![]() ,
,
则![]() ,
,
由(2)知:![]()
![]() ,则
,则![]() ,
,
所以![]() ,故
,故![]() 在
在![]() 上递减,故
上递减,故![]() ;
;
下证![]() ,
,
令![]() 且
且![]() ,则
,则![]() ,
,
当![]() 时
时![]() ,
,![]() 递增,当
递增,当![]() 时
时![]() ,
,![]() 递减,
递减,
所以![]() ,故在
,故在![]() 上
上![]() 恒成立,
恒成立,
则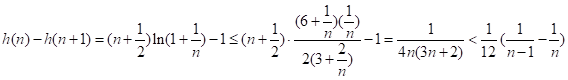 ,
,
所以![]() ,
,![]() ,…,
,…,![]() ,
,
累加得:![]() ,而
,而![]() ,则
,则![]() ,
,
所以![]() ,故
,故![]() ;
;
综上,![]() ,即
,即![]()
