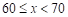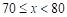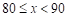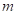2022年贵州黔东南州中考数学试题及答案
一、选择题:(每个小题4分,10个小题共40分)
1. 下列说法中,正确的是( )
A. 2与 互为倒数 B. 2与
互为倒数 B. 2与 互为相反数 C. 0的相反数是0 D. 2的绝对值是
互为相反数 C. 0的相反数是0 D. 2的绝对值是
【答案】C
【解析】
【分析】根据相反数定义,倒数定义,绝对值定义对各选项进行一一判断即可.
【详解】解:A. 2与 互为相反数,故选项A不正确
互为相反数,故选项A不正确
B. 2与 互为倒数,故选项B不正确;
互为倒数,故选项B不正确;
C. 0的相反数是0,故选项C正确;
D. 2的绝对值是2,故选项D不正确.
故选C.
【点睛】本题考查相反数定义,倒数定义,绝对值定义,掌握相关定义是解题关键.
2. 下列运算正确的是( )
A.  B.
B. 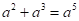
C.  D.
D. 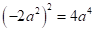
【答案】D
【解析】
【分析】运用同底数幂的除法,合并同类项,去括号法则,积的乘方等知识逐一分析即可
【详解】解:A. ,不符合题意;
,不符合题意;
B. ,不能进行合并同类项,不符合题意;
,不能进行合并同类项,不符合题意;
C.-2(a+b)=-2a-2b,不符合题意;
D. ,符合题意;
,符合题意;
故选:D.
【点睛】本题考查了同底数幂的除法,合并同类项,去括号法则,积的乘方,熟练以上知识是解题的关键.
3. 一个几何体的三视图如图所示,则该几何体为( )
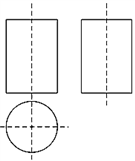
A. 圆柱 B. 圆锥 C. 四棱柱 D. 四棱锥
【答案】A
【解析】
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形,从而得出答案.
【详解】俯视图为圆的几何体为球,圆柱,再根据其他视图,可知此几何体为圆柱.
故选:A.
【点睛】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力.
4. 一块直角三角板按如图所示方式放置在一张长方形纸条上,若 ,则
,则 的度数为( )
的度数为( )
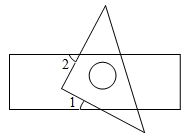
A. 28° B. 56° C. 36° D. 62°
【答案】D
【解析】
【分析】根据矩形的性质得出EF∥GH,过点C作CA∥EF,利用平行线的性质得出∠2=∠MCA,∠1=CAN,然后代入求解即可.
【详解】解:如图所示标注字母,
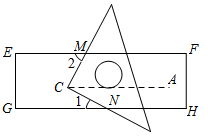
∵四边形EGHF为矩形,
∴EF∥GH,
过点C作CA∥EF,
∴CA∥EF∥GH,
∴∠2=∠MCA,∠1=CAN,
∵∠1=28°,∠MCN=90°,
∴∠2=∠MCA=90°-∠1=62°,
故选:D.
【点睛】题目主要考查矩形的性质,平行线的性质,角度的计算等,理解题意,作出相应辅助线是解题关键.
5. 已知关于 的一元二次方程
的一元二次方程 的两根分别记为
的两根分别记为 ,
, ,若
,若 ,则
,则 的值为( )
的值为( )
A. 7 B.  C. 6 D.
C. 6 D. 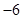
【答案】B
【解析】
【分析】根据根与系数关系求出 =3,a=3,再求代数式的值即.
=3,a=3,再求代数式的值即.
【详解】解:∵一元二次方程 的两根分别记为
的两根分别记为 ,
, ,
,
∴ +
+ =2,
=2,
∵ ,
,
∴ =3,
=3,
∴ ·
· =-a=-3,
=-a=-3,
∴a=3,
∴ .
.
故选B.
【点睛】本题考查一元二次方程的根与系数关系,代数式的值,掌握一元二次方程的根与系数关系,代数式的值是解题关键.
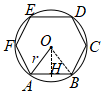
6. 如图,已知正六边形 内接于半径为
内接于半径为 的
的 ,随机地往
,随机地往 内投一粒米,落在正六边形内的概率为( )
内投一粒米,落在正六边形内的概率为( )
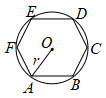
A.  B.
B.  C.
C.  D. 以上答案都不对
D. 以上答案都不对
【答案】A
【解析】
【分析】连接OB,过点O作OH⊥AB于点H,由正六边形的特点可证得△OAB是等边三角形,由特殊角的三角函数值可求出OH的长,利用三角形的面积公式即可求出△OAB的面积,进而可得出正六边形ABCDEF的面积,即可得出结果.
 详解】解:如图:连接OB,过点O作OH⊥AB于点H,
详解】解:如图:连接OB,过点O作OH⊥AB于点H,
∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB=r,
∴△OAB是等边三角形,
∴AB=OA=OB=r,∠OAB=60°,
在 中,
中, ,
,
∴ ,
,
∴正六边形的面积 ,
,
∵⊙O的面积=πr2,
∴米粒落在正六边形内的概率为: ,
,
故选:A.
【点睛】本题考查了正多边形和圆、正六边形的性质、等边三角形的判定与性质、解直角三角形;熟练掌握正六边形的性质,通过作辅助线求出△OAB的面积是解决问题的关键.
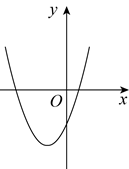
7. 若二次函数 的图像如图所示,则一次函数
的图像如图所示,则一次函数 与反比例函数
与反比例函数 在同一坐标系内的大致图像为( )
在同一坐标系内的大致图像为( )
A.  B.
B.  C.
C.  D.
D. 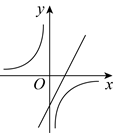
【答案】C
【解析】
【分析】根据二次函数的图像确定a,b,c的正负,即可确定一次函数 所经过的象限和反比例函数
所经过的象限和反比例函数 所在的象限.
所在的象限.
【详解】解:∵二次函数 的图像开口向上,对称轴在y轴左边,与y轴的交点在y轴负半轴,
的图像开口向上,对称轴在y轴左边,与y轴的交点在y轴负半轴,
∴a>0, ,c<0,
,c<0,
∴b>0,-c>0,
∴一次函数 的图像经过第一、二、三象限,反比例函数
的图像经过第一、二、三象限,反比例函数 的图像在第一,三象限,选项C符合题意.
的图像在第一,三象限,选项C符合题意.
故选:C
【点睛】本题考查二次函数图像与系数的关系,一次函数图像与系数的关系,反比例函数图像与系数的关系,熟练并灵活运用这些知识是解题关键.
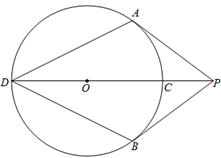
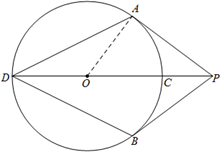
8. 如图, 、
、 分别与
分别与 相切于点
相切于点 、
、 ,连接
,连接 并延长与
并延长与 交于点
交于点 、
、 ,
,
若 ,
, ,则
,则 的值为( )
的值为( )
A.  B.
B.  C.
C.  D.
D. 
【答案】A
【解析】
【分析】连结OA,根据切线长的性质得出PA=PB,OP平分∠APB,OP⊥AP,再证△APD≌△BPD(SAS),然后证明∠AOP=∠ADP+∠OAD=∠ADP+∠BDP=∠ADB, 利用勾股定理求出OP= ,最后利用三角函数定义计算即可.
,最后利用三角函数定义计算即可.
【详解】解:连结OA
∵ 、
、 分别与
分别与 相切于点A、
相切于点A、 ,
,
∴PA=PB,OP平分∠APB,OP⊥AP,
∴∠APD=∠BPD,
在△APD和△BPD中,
 ,
,
∴△APD≌△BPD(SAS)
∴∠ADP=∠BDP,
∵OA=OD=6,
∴∠OAD=∠ADP=∠BDP,
∴∠AOP=∠ADP+∠OAD=∠ADP+∠BDP=∠ADB,
在Rt△AOP中,OP= ,
,
∴sin∠ADB= .
.
故选A.
【点睛】本题考查圆的切线性质,三角形全等判断与性质,勾股定理,锐角三角函数,掌握圆的切线性质,三角形全等判断与性质,勾股定理,锐角三角函数是解题关键.
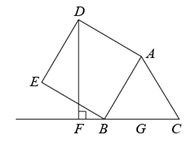
9. 如图,在边长为2 等边三角形
等边三角形 的外侧作正方形
的外侧作正方形 ,过点
,过点 作
作 ,垂足为
,垂足为 ,则
,则 的长为( )
的长为( )
A.  B.
B.  C.
C.  D.
D. 
【答案】D
【解析】
【分析】过点A分别作AG⊥BC于点G,AH⊥DF于点H,可得四边形AGFH是矩形,从而得到FH=AG,再由△ABC为等边三角形,可得∠BAG=30°,BG=1,从而得到 ,再证得∠DAH=∠BAG=30°,然后根据直角三角形的性质,即可求解.
,再证得∠DAH=∠BAG=30°,然后根据直角三角形的性质,即可求解.
【详解】解:如图,过点A分别作AG⊥BC于点G,AH⊥DF于点H,

∵DF⊥BC,
∴∠GFH=∠AHF=∠AGF=90°,
∴四边形AGFH是矩形,
∴FH=AG,
∵△ABC为等边三角形,
∴∠BAC=60°,BC=AB=2,
∴∠BAG=30°,BG=1,
∴ ,
,
∴ ,
,
在正方形ABED中,AD=AB=2,∠BAD=90°,
∴∠DAH=∠BAG=30°,
∴ ,
,
∴ .
.
故选:D
【点睛】本题主要考查了等边三角形和正方形的性质,直角三角形的性质,熟练掌握等边三角形和正方形的性质,直角三角形的性质是解题的关键.
10. 在解决数学实际问题时,常常用到数形结合思想,比如: 的几何意义是数轴上表示数
的几何意义是数轴上表示数 的点与表示数
的点与表示数 的点的距离,
的点的距离, 的几何意义是数轴上表示数
的几何意义是数轴上表示数 的点与表示数2的点的距离.当
的点与表示数2的点的距离.当 取得最小值时,
取得最小值时, 的取值范围是( )
的取值范围是( )
A.  B.
B.  或
或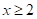 C.
C.  D.
D. 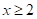
【答案】C
【解析】
【分析】由题意画出数轴,然后根据数轴上的两点距离可进行求解.
【详解】解:如图,由 可得:点
可得:点 、
、 、
、 分别表示数
分别表示数 、2、
、2、 ,
, .
.
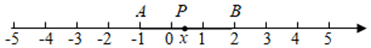
 的几何意义是线段
的几何意义是线段 与
与 的长度之和,
的长度之和,
 当点
当点 在线段
在线段 上时,
上时, ,当点
,当点 在点
在点 的左侧或点
的左侧或点 的右侧时,
的右侧时, .
.
 取得最小值时,
取得最小值时, 的取值范围是
的取值范围是 ;
;
故选C.
【点睛】本题主要考查数轴上的两点距离,解题的关键是利用数形结合思想进行求解.
二、填空题(每个小题3分,10个小题共30分)
11. 有一种新冠病毒直径为0.000000012米,数0.000000012用科学记数法表示为________.
【答案】1.2×10-8
【解析】
【分析】根据绝对值小于1的数可以用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定,即可求解.
【详解】解:0.000000012=1.2×10-8.
故答案为:1.2×10-8
【点睛】本题考查用科学记数法表示较小的数,熟练掌握一般形式为 ,其中
,其中 ,n为由原数左边起第一个不为零的数字前面的0的个数所决定是解题的关键.
,n为由原数左边起第一个不为零的数字前面的0的个数所决定是解题的关键.
12. 分解因式: _______.
_______.
【答案】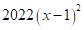
【解析】
【分析】先提公因式,然后再根据完全平方公式可进行因式分解.
【详解】解:原式= ;
;
故答案为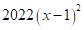 .
.
【点睛】本题主要考查因式分解,熟练掌握因式分解是解题的关键.
13. 某中学在一次田径运动会上,参加女子跳高的7名运动员的成绩如下(单位:m):1.20,1.25,1.10,1.15,1.35,1.30,1.30.这组数据的中位数是_______.
【答案】1.25
【解析】
【分析】先把数据进行排序,再根据中位数的定义求解.
【详解】解:将数据由小到大进行排序得1.10,1.15,1.20,1.25,1.30,1.30,1.35
中位数应为排序后的第四个数,
故答案为:1.25
【点睛】本题考查中位数的定义,解题的关键是熟练掌握中位数的定义.
14. 若 ,则
,则 的值是________.
的值是________.
【答案】9
【解析】
【分析】根据非负数之和为0,每一项都为0,分别算出x,y的值,即可
【详解】∵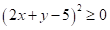
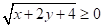
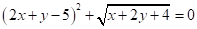
∴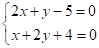
解得: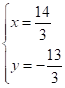
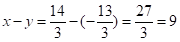
故答案为:9
【点睛】本题考查非负数之和为零,解二元一次方程组;根据非负数之和为零,每一项都为0,算出x,y 值是解题关键
值是解题关键
15. 如图,矩形 的对角线
的对角线 ,
, 相交于点
相交于点 ,
, //
// ,
, //
// .若
.若 ,则四边形
,则四边形 的周长是_______.
的周长是_______.
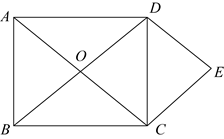
【答案】20
【解析】
【分析】首先由四边形ABCD是矩形,根据矩形的性质,易得OC=OD=5,由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又可判定四边形CODE是菱形,继而求得答案.
【详解】解:∵四边形ABCD是矩形,
∴AC=BD=10,OA=OC,OB=OD,
∴OC=OD= BD=5,
BD=5,
∵ //
// ,
, //
// .,
.,
∴四边形CODE是平行四边形,
∵OC=OD =5,
∴四边形CODE是菱形,
∴四边形CODE的周长为:4OC=4×5=20
故答案为20.
【点睛】本题考查菱形的判定与性质以及矩形的性质.此题难度不大,注意证得四边形CODE是菱形是解题关键.
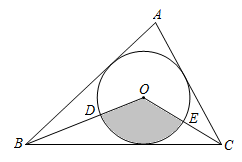
16. 如图,在 中,
中, ,半径为3cm的
,半径为3cm的 是
是 的内切圆,连接
的内切圆,连接 、
、 ,则图中阴影部分的面积是__________cm2.(结果用含
,则图中阴影部分的面积是__________cm2.(结果用含 的式子表示)
的式子表示)
【答案】
【解析】
【分析】根据内切圆圆心是三角形三条角平分线的交点,得到 的大小,然后用扇形面积公式即可求出
的大小,然后用扇形面积公式即可求出
【详解】∵内切圆圆心是三条角平分线的交点
∴ ;
;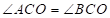
设 ,
,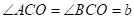
在 中:
中: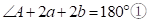
在 中:
中: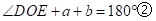
由①②得: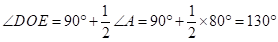
扇形面积: (cm2)
(cm2)
故答案为:
【点睛】本题考查内心的性质,扇形面积计算;解题关键是根据角平分线算出 的度数
的度数
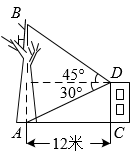
17. 如图,校园内有一株枯死的大树 ,距树12米处有一栋教学楼
,距树12米处有一栋教学楼 ,为了安全,学校决定砍伐该树,站在楼顶
,为了安全,学校决定砍伐该树,站在楼顶 处,测得点
处,测得点 的仰角为45°,点
的仰角为45°,点 的俯角为30°,小青计算后得到如下结论:①
的俯角为30°,小青计算后得到如下结论:① 米;②
米;② 米;③若直接从点
米;③若直接从点 处砍伐,树干倒向教学楼
处砍伐,树干倒向教学楼 方向会对教学楼有影响;④若第一次在距点
方向会对教学楼有影响;④若第一次在距点 的8米处的树干上砍伐,不会对教学楼
的8米处的树干上砍伐,不会对教学楼 造成危害.其中正确的是_______.(填写序号,参考数值:
造成危害.其中正确的是_______.(填写序号,参考数值: ,
, )
)
【答案】①③④
【解析】
【分析】过点D的水平线交AB于E,先证四边形EACD为矩形,ED=AC=12米,①利用三角函数求出AB=BE+AE=DEtan45°+DEtan30°,②利用CD=AE=DEtan30°=4 米, ③利用AB=18.8米>12米,④点B到砍伐点的距离为:18.8-8=10.8<12,判断即可.
米, ③利用AB=18.8米>12米,④点B到砍伐点的距离为:18.8-8=10.8<12,判断即可.
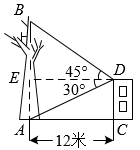
【详解】解:过点D的水平线交AB于E,
∵DE∥AC,EA∥CD,∠DCA=90°,
∴四边形EACD为矩形,
∴ED=AC=12米,
①AB=BE+AE=DEtan45°+DEtan30°=12+4 故①正确;
故①正确;
②∵CD=AE=DEtan30°=4 米,故②不正确;
米,故②不正确;
③∵AB=18.8米>12米,∴直接从点A处砍伐,树干倒向教学楼 方向会对教学楼有影响;故③正确;
方向会对教学楼有影响;故③正确;
④∵第一次在距点A的8米处的树干上砍伐,
∴点B到砍伐点的距离为:18.8-8=10.8<12,
∴第一次在距点A的8米处的树干上砍伐,不会对教学楼 造成危害.故④正确
造成危害.故④正确
∴其中正确的是①③④.
故答案为①③④.
【点睛】本题考查解直角三角形,矩形的判断与性质,掌握解直角三角形方法,矩形的判断与性质是解题关键.
18. 在平面直角坐标系中,将抛物线 先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是_______.
先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是_______.
【答案】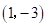
【解析】
【分析】先把抛物线配方为顶点式,求出定点坐标,求出旋转后的抛物线,再根据“上加下减,左加右减”的法则进行解答即可.
【详解】解:∵ ,
,
∴抛物线的顶点为(-1,-2),
将抛物线 先绕原点旋转180°抛物线顶点为(1,2),
先绕原点旋转180°抛物线顶点为(1,2),
旋转后的抛物线为 ,
,
再向下平移5个单位, 即
即 .
.
∴新抛物线的顶点(1,-3)
故答案是:(1,-3).
【点睛】本题考查的是抛物线的图象与几何变换,熟知函数图象旋转与平移的法则是解答此题的关键.
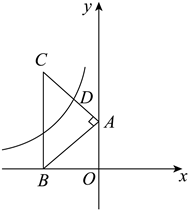
19. 如图,在平面直角坐标系中,等腰直角三角形 的斜边
的斜边 轴于点
轴于点 ,直角顶点
,直角顶点 在
在 轴上,双曲线
轴上,双曲线 经过
经过 边的中点
边的中点 ,若
,若 ,则
,则 ______.
______.
【答案】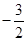
【解析】
【分析】根据 是等腰直角三角形,
是等腰直角三角形, 轴,得到
轴,得到 是等腰直角三角形,再根据
是等腰直角三角形,再根据 求出 A点,C点坐标,根据中点公式求出D点坐标,将D点坐标代入反比例
求出 A点,C点坐标,根据中点公式求出D点坐标,将D点坐标代入反比例
函数解析式即可求得k.
【详解】∵ 是等腰直角三角形,
是等腰直角三角形, 轴.
轴.
∴ ;
; .
.
∴ 是等腰直角三角形.
是等腰直角三角形.
∴ .
.
故: ,
, .
.
 .
.
将D点坐标代入反比例函数解析式.
 .
.
故答案为: .
.
【点睛】本题考查平面几何与坐标系综合,反比例函数解析式;本体解题关键是得到 是等腰直角三角形,用中点公式算出D点坐标.
是等腰直角三角形,用中点公式算出D点坐标.
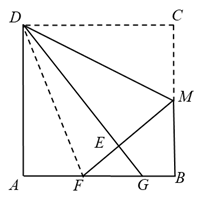
20. 如图,折叠边长为4cm的正方形纸片 ,折痕是
,折痕是 ,点
,点 落在点
落在点 处,分别延长
处,分别延长 、
、 交
交 于点
于点 、
、 ,若点
,若点 是
是 边的中点,则
边的中点,则 ______cm.
______cm.
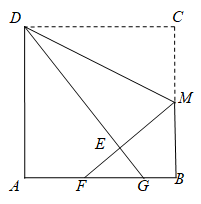
【答案】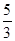
【解析】
【分析】根据折叠的性质可得DE=DC=4,EM=CM=2,连接DF,设FE=x,由勾股定理得BF,DF,从而求出x的值,得出FB,再证明 ,利用相似三角形对应边成比例可求出FG.
,利用相似三角形对应边成比例可求出FG.
【详解】解:连接 如图,
如图,
∵四边形ABCD是正方形,
∴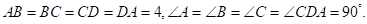
∵点M为BC的中点,
∴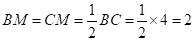
由折叠得, ∠
∠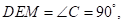
∴∠ ,
,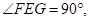
设 则有
则有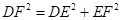
∴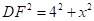
又在 中,
中, ,
,
∵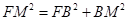
∴
∴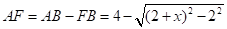
在 中,
中,
∴
解得, (舍去)
(舍去)
∴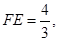
∴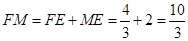
∴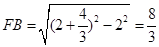
∵∠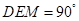
∴∠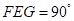
∴∠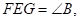
又∠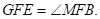
∴△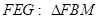
∴ 即
即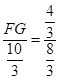
∴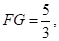
故答案为: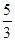
【点睛】本题主要考查了正方形的性质,折叠的性质,勾股定理,相似三角形的判定与性质,正确作出辅助线是解答本题的关键.
三、解答题(6个小题,共80分)
21. (1)计算: ;
;
(2)先化简,再求值: ,其中
,其中 .
.
【答案】(1) ;(2)
;(2)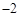
【解析】
【分析】(1)先每项化简,再加减算出最终结果即可;
(2)先因式分解,化除为乘,通分,化简;再带入数值计算即可.
【详解】(1)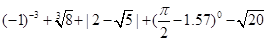
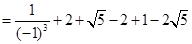
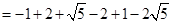
 ;
;
(2)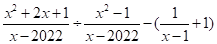
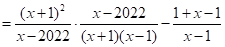
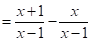
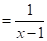
∵ ,
,
∴原式= .
.
【点睛】本题考查了实数的混合运算,分式的化简求值,二次根式的性质,特殊角的三角函数值,零指数幂和负整数指数幂的意义,熟练掌握各知识点是解答本题的关键.
22. 某县教育局印发了上级主管部门的“法治和安全等知识”学习材料,某中学经过一段时间的学习,同学们都表示有了提高,为了解具体情况,综治办开展了一次全校性竞赛活动,王老师抽取了这次竞赛中部分同学的成绩,并绘制了下面不完整的统计图、表.
参赛成绩 |
|
|
|
|
人数 | 8 |
|
| 32 |
级别 | 及格 | 中等 | 良好 | 优秀 |
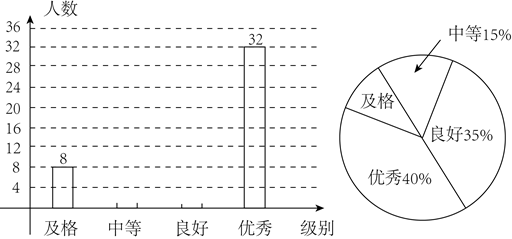
请根据所给的信息解答下列问题:
(1)王老师抽取了_______名学生的参赛成绩;抽取的学生的平均成绩是_______分;
(2)将条形统计图补充完整;
(3)若该校有1600名学生,请估计竞赛成绩在良好以上 的学生有多少人?
的学生有多少人?
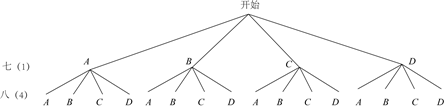
(4)在本次竞赛中,综治办发现七(1)班、八(4)班的成绩不理想,学校要求这两个班
加强学习一段时间后,再由电脑随机从A、B、C、D四套试卷中给每班派发一套试卷进行测试,请用列表或画树状图的方法求出两个班同时选中同一套试卷的概率.
【答案】(1)80;85.5(答案不唯一)
(2)见详解 (3)1200人
(4)两个班同时选中同一套试卷的概率为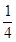
【解析】
【分析】(1)利用条形图优秀人数÷优秀人数所占百分比求出样本容量,利用加权平均数计算即可;
(2)求出中等人数与良好人数,补画条形图即可;
(3)先求出样本中良好以上 百分比,再用样本的百分比×该校总人数计算即可;
百分比,再用样本的百分比×该校总人数计算即可;
(4)画树状图,列举所有等可能情况,从中找出满足条件的情况4种,利用概率公式计算即可.
【小问1详解】
解:根据条形图优秀有32人,由扇形统计图知优秀占40%,
∴王老师抽取了32÷40%=80名学生的参赛成绩;
∴m=80×15%=12人,n=80×35%=28人;
抽取的学生的平均成绩是65×10%+75×15%+85×35%+95×40%=85.5分,
故80;85.5(答案不唯一);
【小问2详解】
解:∵中等人生为12人,良好人数为28人,补画条形图如图,
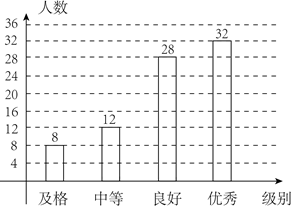
【小问3详解】
解:在样本中良好以上占40%+35%=75%,
∴该校有1600名学生,请估计竞赛成绩在良好以上 的学生有1600×75%=1200人;
的学生有1600×75%=1200人;
【小问4详解】
解:画树状图列举所有等可能的情况共有16种,其中两班都考同一试卷的情况有4种,
两个班同时选中同一套试卷的概率为 .
.
【点睛】本题考查从条形图与扇形图获取信息与处理信息,样本容量,加权平均数,画条形图,用样本 百分比含量估计总体中的数量,画树状图求概率,掌握从条形图与扇形图获取信息与处理信息,样本容量,加权平均数,画条形图,用样本的百分比含量估计总体中的数量,画树状图求概率是解题关键.
百分比含量估计总体中的数量,画树状图求概率,掌握从条形图与扇形图获取信息与处理信息,样本容量,加权平均数,画条形图,用样本的百分比含量估计总体中的数量,画树状图求概率是解题关键.
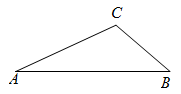
23. (1)请在图中作出 的外接圆
的外接圆 (尺规作图,保留作图痕迹,不写作法);
(尺规作图,保留作图痕迹,不写作法);
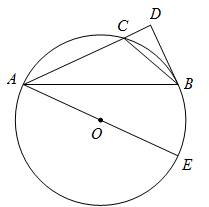
(2)如图, 是
是 的外接圆,
的外接圆, 是
是 的直径,点
的直径,点 是
是 的中点,过点
的中点,过点 的切线与
的切线与 的延长线交于点
的延长线交于点 .
.
①求证: ;
;
②若 ,
, ,求
,求 的半径.
的半径.
【答案】(1)见详解
(2)
① 见详解
② 5
【解析】
【分析】(1)做AB、AC的垂直平分线交于点O,以OB为半径,以O为圆心做圆即可得到 的外接圆;
的外接圆;
(2)①证明 即可证明
即可证明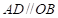 ,从而证得
,从而证得 ;
;
② 证明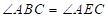 ,根据
,根据 得正切求得EC,再根据勾股定理求得AE.
得正切求得EC,再根据勾股定理求得AE.
【详解】(1)如下图所示
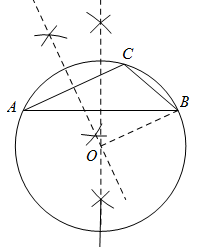
∵ 的外接圆
的外接圆 的圆心为任意两边的垂直平分线的交点,半径为交点到任意顶点的距离,
的圆心为任意两边的垂直平分线的交点,半径为交点到任意顶点的距离,
∴做AB、AC的垂直平分线交于点O,以OB为半径,以O为圆心做圆即可得到 的外接圆;
的外接圆;
(2)
①如下图所示,连接OC、OB
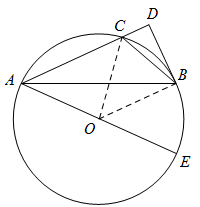
∵BD是 的切线
的切线
∴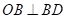
∵ 是
是 对应的圆周角,
对应的圆周角, 是
是 对应的圆心角
对应的圆心角
∴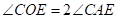
∵点 是
是 的中点
的中点
∴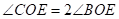
∴
∴
∴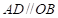
∴
②如下图所示,连接CE
∵ 与
与 是
是 对应的圆周角
对应的圆周角
∴
∵ 是
是 的直径
的直径
∴
∴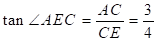
∴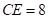
∵
∴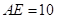
∴ 的半径为
的半径为 .
.
【点睛】本体考查圆、直角三角形的性质,解题的关键是掌握圆和直角三角形的相关知识.
24. 某快递公司为了加强疫情防控需求,提高工作效率,计划购买A、B两种型号的机器人来搬运货物,已知每台A型机器人比每台B型机器人每天少搬运10吨,且A型机器人每天搬运540吨货物与B型机器人每天搬运600吨货物所需台数相同.
(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?
(2)每台A型机器人售价1.2万元,每台B型机器人售价2万元,该公司计划采购A、B两种型号的机器人共30台,必须满足每天搬运的货物不低于2830吨,购买金额不超过48万元.
请根据以上要求,完成如下问题:
①设购买A型机器人 台,购买总金额为
台,购买总金额为 万元,请?p>
2022年?5" src="//img.985ks.com/images_new/img_default_show.png" data-src="//img.985ks.com/uploadfile/images/2023/0206/16756867287351438.png" width="16"/>与
万元,请?p>
2022年?5" src="//img.985ks.com/images_new/img_default_show.png" data-src="//img.985ks.com/uploadfile/images/2023/0206/16756867287351438.png" width="16"/>与 的函数关系式;
的函数关系式;
②请你求出最节省的采购方案,购买总金额最低是多少万元?
【答案】(1)每台A型机器人每天搬运货物90吨,每台B型机器人每天搬运货物为100吨.
(2)① ;②当购买A型机器人17台,B型机器人13台时,购买总金额最少,最少金额为46.4万元.
;②当购买A型机器人17台,B型机器人13台时,购买总金额最少,最少金额为46.4万元.
【解析】
【分析】(1)设每台A型机器人每天搬运货物x吨,则每台B型机器人每天搬运货物为(x+10)吨,然后根据题意可列分式方程进行求解;
(2)①由题意可得购买B型机器人的台数为 台,然后由根据题意可列出函数关系式;②由题意易得
台,然后由根据题意可列出函数关系式;②由题意易得 ,然后可得
,然后可得 ,进而根据一次函数的性质可进行求解.
,进而根据一次函数的性质可进行求解.
【小问1详解】
解:设每台A型机器人每天搬运货物x吨,则每台B型机器人每天搬运货物为(x+10)吨,由题意得:
 ,
,
解得: ;
;
经检验: 是原方程的解;
是原方程的解;
答:每台A型机器人每天搬运货物90吨,每台B型机器人每天搬运货物为100吨.
【小问2详解】
解:①由题意可得:购买B型机器人的台数为 台,
台,
∴ ;
;
②由题意得: ,
,
解得: ,
,
∵-0.8<0,
∴w随m的增大而减小,
∴当m=17时,w有最小值,即为 ,
,
答:当购买A型机器人17台,B型机器人13台时,购买总金额最少,最少金额为46.4万元.
【点睛】本题主要考查分式方程的应用、一元一次不等式组的应用及一次函数的应用,熟练掌握分式方程的应用、一元一次不等式组的应用及一次函数的应用是解题的关键.
25. 阅读材料:小明喜欢探究数学问题,一天杨老师给他这样一个几何问题:
如图, 和
和 都是等边三角形,点
都是等边三角形,点 在
在 上.
上.
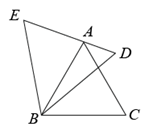
求证:以 、
、 、
、 为边的三角形是钝角三角形.
为边的三角形是钝角三角形.
(1)【探究发现】小明通过探究发现:连接 ,根据已知条件,可以证明
,根据已知条件,可以证明 ,
, ,从而得出
,从而得出 为钝角三角形,故以
为钝角三角形,故以 、
、 、
、 为边的三角形是钝角三角形.
为边的三角形是钝角三角形.
请你根据小明的思路,写出完整的证明过程.
(2)【拓展迁移】如图,四边形 和四边形
和四边形 都是正方形,点
都是正方形,点 在
在 上.
上.
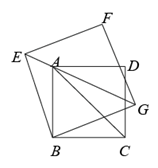
①试猜想:以 、
、 、
、 为边的三角形的形状,并说明理由.
为边的三角形的形状,并说明理由.
②若 ,试求出正方形
,试求出正方形 的面积.
的面积.
【答案】(1)钝角三角形;证明见详解
(2)①直角三角形;证明见详解;②S四边形ABCD=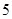
【解析】
【分析】(1)根据等边三角形性质得出,BE=BD,AB=CB,∠EBD=∠ABC=60°,再证△EBA≌△DBC(SAS)∠AEB=∠CDB=60°,AE=CD,求出∠ADC=∠ADB+∠BDC=120°,可得△ADC为钝角三角形即可;
(2)①以 、
、 、
、 为边的三角形是直角三角形,连结CG,根据正方形性质,得出∠EBG=∠ABC,EB=GB,AB=CB,∠BEA=∠BGE=45°,再证△EBA≌△GBC(SAS)得出AE=CG,∠BEA=∠BGC=45°,可证△AGC为直角三角形即可;②连结BD,根据勾股定理求出AC=
为边的三角形是直角三角形,连结CG,根据正方形性质,得出∠EBG=∠ABC,EB=GB,AB=CB,∠BEA=∠BGE=45°,再证△EBA≌△GBC(SAS)得出AE=CG,∠BEA=∠BGC=45°,可证△AGC为直角三角形即可;②连结BD,根据勾股定理求出AC= ,然后利用正方形的面积公式求解即可.
,然后利用正方形的面积公式求解即可.
【小问1详解】
证明:∵△ABC与△EBD均为等边三角形,
∴BE=BD,AB=CB,∠EBD=∠ABC=60°,
∴∠EBA+∠ABD=∠ABD+∠DBC,
∴∠EBA=∠DBC,
在△EBA和△DBC中,
 ,
,
∴△EBA≌△DBC(SAS),
∴∠AEB=∠CDB=60°,AE=CD,
∴∠ADC=∠ADB+∠BDC=120°,
∴△ADC为钝角三角形,
∴以 、
、 、
、 为边的三角形是钝角三角形.
为边的三角形是钝角三角形.
 【小问2详解】
【小问2详解】
证明:①以 、
、 、
、 为边的三角形是直角三角形.
为边的三角形是直角三角形.
连结CG,
∵四边形 和四边形
和四边形 都是正方形,
都是正方形,
∴∠EBG=∠ABC,EB=GB,AB=CB,
∵EG为正方形的对角线,
∴∠BEA=∠BGE=45°,
∴∠EBA+∠ABG=∠ABG+∠GBC=90°,
∴∠EBA=∠GBC,
在△EBA和△GBC中,
 ,
,
∴△EBA≌△GBC(SAS),
∴AE=CG,∠BEA=∠BGC=45°,
∴∠AGC=∠AGB+∠BGC=45°+45°=90°,
∴△AGC为直角三角形,
∴以 、
、 、
、 为边的三角形是直角三角形;
为边的三角形是直角三角形;
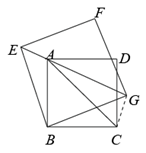
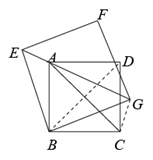
②连结BD,
∵△AGC为直角三角形, ,
,
∴AC= ,
,
∴四边形ABCD为正方形,
∴AC=BD= ,
,
∴S四边形ABCD= .
.
【点睛】本题考查等边三角形的性质,三角形全等判定与性质,正方形的性质,勾股定理,掌握等边三角形的性质,三角形全等判定与性质,正方形的性质,勾股定理是解题关键.
26. 如图,抛物线 的对称轴是直线
的对称轴是直线 ,与
,与 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点 ,连接
,连接 .
.
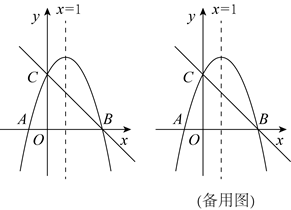
(1)求此抛物线的解析式;
(2)已知点 是第一象限内抛物线上的一个动点,过点
是第一象限内抛物线上的一个动点,过点 作
作 轴,垂足为点
轴,垂足为点 ,
, 交直线
交直线 于点
于点 ,是否存在这样的点
,是否存在这样的点 ,使得以
,使得以 ,
, ,
, 为顶点的三角形是等腰三角形.若存在,请求出点
为顶点的三角形是等腰三角形.若存在,请求出点 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)已知点 是抛物线对称轴上的点,在坐标平面内是否存在点
是抛物线对称轴上的点,在坐标平面内是否存在点 ,使以点
,使以点 、
、 、
、 、
、 为顶点的四边形为矩形,若存在,请直接写出点
为顶点的四边形为矩形,若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)
(2)存在这样的点 (2,1)或
(2,1)或 或
或 ,使得以
,使得以 ,
, ,
, 为顶点的三角形是等腰三角形
为顶点的三角形是等腰三角形
(3)存在点 的坐标为(4,1)或(-2,1)或
的坐标为(4,1)或(-2,1)或 或
或 .
.
【解析】
【分析】(1)根据抛物线的对称轴是直线 ,可得a=-1,再把点
,可得a=-1,再把点 代入,即可求解;
代入,即可求解;
(2)先求出 ,设点N(m,-m+3),可得
,设点N(m,-m+3),可得 ,
, ,再分三种情况讨论:当AC=AN时,当AC=CN时,当AN=CN时,即可求解;
,再分三种情况讨论:当AC=AN时,当AC=CN时,当AN=CN时,即可求解;
(3)设点E(1,n),点F(s,t),然后分两种情况讨论:当BC为边时,当BC为对角线时,即可求解.
【小问1详解】
解:∵抛物线 的对称轴是直线
的对称轴是直线 ,
,
∴ ,解得:a=-1,
,解得:a=-1,
∵抛物线过点 ,
,
∴ ,解得:c=3,
,解得:c=3,
∴抛物线解析式为 ;
;
【小问2详解】
解:存在这样的点 ,使得以
,使得以 ,
, ,
, 为顶点的三角形是等腰三角形.理由如下:
为顶点的三角形是等腰三角形.理由如下:
令y=0,则 ,
,
解得: ,
,
∴点A的坐标为(-1,0),
∴OA=1,
当x=0时,y=3,
∴点C的坐标为(0,3),即OC=3,
∴ ,
,
设直线BC的解析式为 ,
,
把点B(3,0),C(0,3)代入得:
 ,解得:
,解得: ,
,
∴直线BC的解析式为 ,
,
设点N(m,-m+3),
∴MN=-m+3,AM=m+1,
∴ ,
, ,
,
当AC=AN时, ,
,
解得:m=2或0(舍去),
∴此时点N(2,1);
当AC=CN时, ,
,
解得: 或
或 (舍去),
(舍去),
∴此时点N ;
;
当AN=CN时, ,
,
解得: ,
,
∴此时点N ;
;
综上所述,存在这样的点 (2,1)或
(2,1)或 或
或 ,使得以
,使得以 ,
, ,
, 为顶点的三角形是等腰三角形;
为顶点的三角形是等腰三角形;
【小问3详解】
解:存在,理由如下:
∵点B(3,0),C(0,3),
∴OB=OC,
∴BC ,
,
设点E(1,n),点F(s,t),
当BC为边时,点C向右平移3个单位向下平移3个单位得到点B,同样E(F)向右平移3个单位向下平移3个单位得到点F(E),且BE=CF(CE=BF),如图,
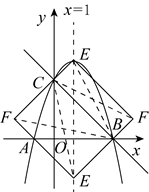
∴ 或
或 ,
,
解得: 或
或 ,
,
∴此时点F的坐标为(4,1)或(-2,1);
当BC为对角线时,BC=EF,且EF与BC的中点重合,如图,
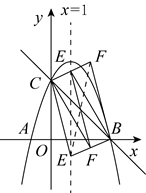
 ,解得:
,解得: 或
或 ,
,
∴此时点F的坐标为 或
或 ;
;
综上所述,存在点 的坐标为(4,1)或(-2,1)或
的坐标为(4,1)或(-2,1)或 或
或 .
.
【点睛】本题主要考查了二次函数的综合题,熟练掌握二次函数的图象和性质,等腰三角形的性质,矩形的性质,并利用分类讨论思想解答是解题的关键是解题的关键