2022年北京中考数学试卷试题及答案
第一部分选择题
一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.
1. 下面几何体中,是圆锥的为()
A.  B.
B. 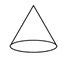
C. 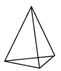 D.
D. 
【参考答案】B
2. 截至2021年12月31日,长江干流六座梯级水电站全年累计发电量达2628.83亿千瓦时,相当于减排二氧化碳约2.2亿吨.将262 883 000 000用科学计数法表示应为()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【参考答案】B
3. 如图,利用工具测量角,则![]() 的大小为()
的大小为()
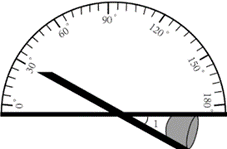
A. 30° B. 60° C. 120° D. 150°
【参考答案】A
4. 实数![]() 在数轴上的对应点的位置如图所示,下列结论中正确的是()
在数轴上的对应点的位置如图所示,下列结论中正确的是()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【参考答案】D
5. 不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【参考答案】A
6. 若关于![]() 的一元二次方程
的一元二次方程![]() 有两个相等的实数根,则实数
有两个相等的实数根,则实数![]() 的值为()
的值为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【参考答案】C
7. 图中的图形为轴对称图形,该图形的对称轴的条数为()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【参考答案】D
8. 下面的三个问题中都有两个变量:
①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;
②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;
③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x,其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是()
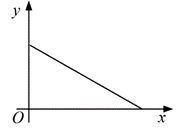
A. ①② B. ①③ C. ②③ D. ①②③
【参考答案】A
第二部分非选择题
二、填空题(共16分,每题2分)
9. 若![]() 在实数范围内有意义,则实数x的取值范围是___________.
在实数范围内有意义,则实数x的取值范围是___________.
【参考答案】x≥8
【详解】解:由题意得:
x-8≥0,
解得:x≥8.
故答案为:x≥8.
10. 分解因式:![]() ______.
______.
【参考答案】![]()
【详解】![]()
![]()
![]()
故答案为:![]() .
.
11. 方程![]() 的解为___________.
的解为___________.
【参考答案】x=5
【详解】解:![]()
方程的两边同乘x(x+5),得:2x=x+5, 解得:x=5, 经检验:把x=5代入x(x+5)=50≠0. 故原方程的解为:x=5
12. 在平面直角坐标系![]() 中,若点
中,若点![]() 在反比例函数
在反比例函数![]() 的图象上,则
的图象上,则![]() ______
______![]() (填“>”“=”或“<”)
(填“>”“=”或“<”)
【参考答案】>
【详解】解:∵k>0,
∴在每个象限内,y随x的增大而减小,
![]() ,
,
∴![]() >
>![]() .
.
故答案为:>.
13. 某商场准备进400双滑冰鞋,了解了某段时间内销售的40双滑冰鞋的鞋号,数据如下:
鞋号 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
销售量/双 | 2 | 4 | 5 | 5 | 12 | 6 | 3 | 2 | 1 |
根据以上数据,估计该商场进鞋号需求最多的滑冰鞋的数量为________双.
【参考答案】120
【详解】解:根据题意得:39码的鞋销售量为12双,销售量最高,
∴该商场进鞋号需求最多的滑冰鞋的数量为![]() 双.
双.
故答案为:120
14. 如图,在![]() 中,
中,![]() 平分
平分![]() 若
若![]() 则
则![]() ____.
____.
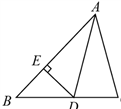
【参考答案】1
【详解】解:如图,作![]() 于点F,
于点F,
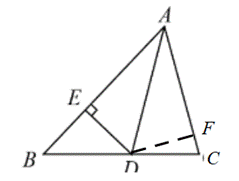
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:1.
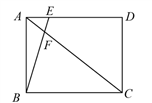
15. 如图,在矩形![]() 中,若
中,若![]() ,则
,则![]() 的长为_______.
的长为_______.
【参考答案】1
【详解】解:在矩形![]() 中:
中:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:1.
16. 甲工厂将生产的I号、II号两种产品共打包成5个不同的包裹,编号分别为A,B,C,D,E,每个包裹的重量及包裹中I号、II号产品的重量如下:
包裹编号 | I号产品重量/吨 | II号产品重量/吨 | 包裹的重量/吨 |
A | 5 | 1 | 6 |
B | 3 | 2 | 5 |
C | 2 | 3 | 5 |
D | 4 | 3 | 7 |
E | 3 | 5 | 8 |
甲工厂准备用一辆载重不超过19.5吨的货车将部分包裹一次运送到乙工厂.
(1)如果装运的I号产品不少于9吨,且不多于11吨,写出一中满足条件的装运方案________(写出要装运包裹的编号);
(2)如果装运的I号产品不少于9吨,且不多于11吨,同时装运的II号产品最多,写出满足条件的装运方案________(写出要装运包裹的编号).
【参考答案】 ①. ABC(或ABE或AD或ACD或BCD) ②. ABE或BCD
【详解】解:(1)根据题意,
选择ABC时,装运的I号产品重量为:![]() (吨),总重
(吨),总重![]() (吨),符合要求;
(吨),符合要求;
选择ABE时,装运的I号产品重量为:![]() (吨),总重
(吨),总重![]() (吨),符合要求;
(吨),符合要求;
选择AD时,装运![]() I号产品重量为:
I号产品重量为:![]() (吨),总重
(吨),总重![]() (吨),符合要求;
(吨),符合要求;
选择ACD时,装运的I号产品重量为:![]() (吨),总重
(吨),总重![]() (吨),符合要求;
(吨),符合要求;
选择BCD时,装运的I号产品重量为:![]() (吨),总重
(吨),总重![]() (吨),符合要求;
(吨),符合要求;
选择DCE时,装运的I号产品重量为:![]() (吨),总重
(吨),总重![]() (吨),不符合要求;
(吨),不符合要求;
选择BDE时,装运的I号产品重量为:![]() (吨),总重
(吨),总重![]() (吨),不符合要求;
(吨),不符合要求;
综上,满足条件的装运方案有ABC或ABE或AD或ACD或BCD.
故答案为:ABC(或ABE或AD或ACD或BCD).
(2)选择ABC时,装运的II号产品重量为:![]() (吨);
(吨);
选择ABE时,装运的II号产品重量为:![]() (吨);
(吨);
选择AD时,装运的II号产品重量为:![]() (吨);
(吨);
选择ACD时,装运的II号产品重量为:![]() (吨);
(吨);
选择BCD时,装运的II号产品重量为:![]() (吨);
(吨);
故答案为:ABE或BCD.
三、解答题(共68分,第17-20题,每题5分,第21题6分,第22题5分,第23-24题,每题6分,第25题5分,第26题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.
17. 计算:![]()
【参考答案】4
【详解】解:![]()
![]()
![]() .
.
【点睛】本题考查了实数的混合运算,掌握零次幂、特殊角的正弦值、二次根式的化简及去绝对值是解题的关键.
18. 解不等式组: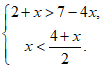
【参考答案】![]()
【详解】解: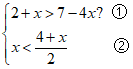
解不等式①得![]() ,
,
解不等式②得![]() ,
,
故所给不等式组的解集为:![]() .
.
19. 已知![]() ,求代数式
,求代数式![]() 的值.
的值.
【参考答案】5
【详解】解:∵![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]()
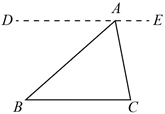
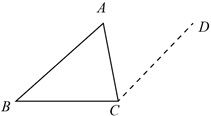
20. 下面是证明三角形内角和定理的两种添加辅助线的方法,选择其中一种,完成证明.
已知:如图, 求证: | |
方法一 证明:如图,过点A作
| 方法二 证明:如图,过点C作 |
【参考答案】答案见解析
【详解】证明:过点![]() 作
作![]() ,
,
则![]() ,
,![]() .
.![]() 两直线平行,内错角相等)
两直线平行,内错角相等)
![]() 点
点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,
![]() .(平角的定义)
.(平角的定义)
![]() .
.
即三角形的内角和为![]() .
.
21. 如图,在![]() 中,
中,![]() 交于点
交于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() .
.
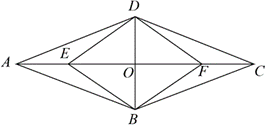
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 求证:四边形
求证:四边形![]() 是菱形.
是菱形.
【参考答案】(1)见解析(2)见解析
【小问1详解】
证明:∵四边形ABCD为平行四边形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
【小问2详解】
∵四边形ABCD为平行四边形,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴四边形ABCD为菱形,
∴![]() ,
,
即![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴四边形![]() 是菱形.
是菱形.
22. 在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .
.
(1)求该函数的解析式及点![]() 的坐标;
的坐标;
(2)当![]() 时,对于
时,对于![]() 的每一个值,函数
的每一个值,函数![]() 的值大于函数
的值大于函数![]() 的值,直接写出
的值,直接写出![]() 的取值范围.
的取值范围.
【参考答案】(1)![]() ,
,![]()
(2)![]()
【小问1详解】
解:将![]() ,
,![]() 代入函数解析式得,
代入函数解析式得,
![]() ,解得
,解得![]() ,
,
∴函数![]() 解析式为:
解析式为:![]() ,
,
当![]() 时,得
时,得![]() ,
,
∴点A的坐标为![]() .
.
【小问2详解】
由题意得,
![]() ,即
,即![]() ,
,
又由![]() ,得
,得![]() ,
,
解得![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.
23. 某校举办“歌唱祖国”演唱比赛,十位评委对每位同学的演唱进行现场打分,对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析,下面给出了部分信息.
a.甲、乙两位同学得分的折线图:
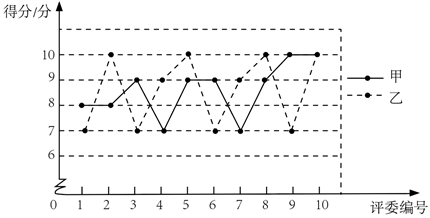
b.丙同学得分:
10,10,10,9,9,8,3,9,8,10
c.甲、乙、丙三位同学得分的平均数:
同学 | 甲 | 乙 | 丙 |
平均数 | 8.6 | 8.6 | m |
根据以上信息,回答下列问题:
(1)求表中m的值;
(2)在参加比赛的同学中,如果某同学得分的10个数据的方差越小,则认为评委对该同学演唱的评价越一致.据此推断:甲、乙两位同学中,评委对_________的评价更一致(填“甲”或“乙”);
(3)如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分,最后得分越高,则认为该同学表现越优秀.据此推断:在甲、乙、丙三位同学中,表现最优秀的是_________(填“甲”“乙”或“丙”).
【参考答案】(1)![]()
(2)甲(3)乙
【小问1详解】
解:丙的平均数:![]() ,
,
则![]() .
.
【小问2详解】
![]() ,
,
![]() ,
,
![]() ,
,
∴甲、乙两位同学中,评委对甲的评价更一致,
故答案为:甲.
【小问3详解】
由题意得,去掉一个最高分和一个最低分后的平均分为:
甲:![]() ,
,
乙:![]() ,
,
丙:![]() ,
,
∵去掉一个最高分和一个最低分后乙的平均分最高,
因此最优秀的是乙,
故答案为:乙.
24. 如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的一条弦,
的一条弦,![]() 连接
连接![]()
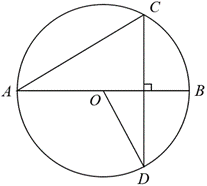
(1)求证:![]()
(2)连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点,求证:直线
的中点,求证:直线![]() 为
为![]() 的切线.
的切线.
【参考答案】(1)答案见解析
(2)答案见解析
【小问1详解】
证明:设![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,

由题可知,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
【小问2详解】
证明:![]()
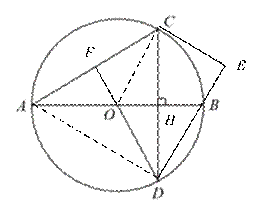
连接![]() ,
,
![]() ,
,
![]() ,
,
同理可得:![]() ,
,![]() ,
,
∵点H是CD的中点,点F是AC的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为
为![]() 的直径,
的直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 为
为![]() 的切线.
的切线.
25. 单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台,运动员起跳后的飞行路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度![]() (单位:m)与水平距离
(单位:m)与水平距离![]() (单位:m)近似满足函数关系
(单位:m)近似满足函数关系![]() .
.
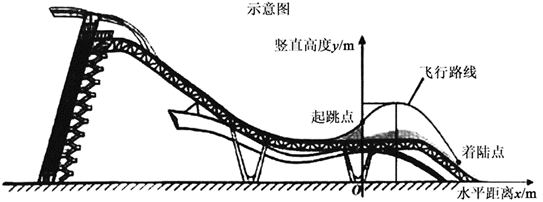
某运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离![]() 与竖直高度
与竖直高度![]() 的几组数据如下:
的几组数据如下:
水平距离x/m | 0 | 2 | 5 | 8 | 11 | 14 |
竖直高度y/m | 20.00 | 21.40 | 22.75 | 23.20 | 22.75 | 21.40 |
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系![]()
(2)第二次训练时,该运动员的竖直高度y与水平距离x近似满足函数关系![]() 记该运动员第一次训练的着陆点的水平距离为d1,第二次训练的着陆点的水平距离为
记该运动员第一次训练的着陆点的水平距离为d1,第二次训练的着陆点的水平距离为![]() ,则
,则![]() ______
______![]() (填“>”“=”或“<”).
(填“>”“=”或“<”).
【参考答案】(1)23.20m;![]()
(2)![]()
【小问1详解】
解:根据表格中的数据可知,抛物线的顶点坐标为:![]() ,
,
∴![]() ,
,![]() ,
,
即该运动员竖直高度的最大值为23.20m,
根据表格中的数据可知,当![]() 时,
时,![]() ,代入
,代入![]() 得:
得:
![]() ,解得:
,解得:![]() ,
,
∴函数关系关系式为:![]() .
.
【小问2详解】
设着陆点的纵坐标为![]() ,则第一次训练时,
,则第一次训练时,![]() ,
,
解得:![]() 或
或![]() ,
,
∴根据图象可知,第一次训练时着陆点的水平距离![]() ,
,
第二次训练时,![]() ,
,
解得:![]() 或
或![]() ,
,
∴根据图象可知,第二次训练时着陆点的水平距离![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:![]() .
.
26. 在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() 上,设抛物线的对称轴为
上,设抛物线的对称轴为![]()
(1)当![]() 时,求抛物线与y轴交点
时,求抛物线与y轴交点![]() 坐标及
坐标及![]() 的值;
的值;
(2)点![]() 在抛物线上,若
在抛物线上,若![]() 求
求![]() 的取值范围及
的取值范围及![]() 的取值范围.
的取值范围.
【参考答案】(1)(0,2);2
(2)![]()
![]() 取值范围为
取值范围为![]() ,
,![]() 的取值范围为
的取值范围为![]()
【小问1详解】
解:当![]() 时,
时,![]() ,
,
∴当x=0时,y=2,
∴抛物线与y轴交点的坐标为(0,2);
∵![]() ,
,
∴点![]() 关于对称轴为
关于对称轴为![]() 对称,
对称,
∴![]() ;
;
【小问2详解】
解:当x=0时,y=c,
∴抛物线与y轴交点坐标为(0,c),
∴抛物线与y轴交点关于对称轴![]() 的对称点坐标为(2t,c),
的对称点坐标为(2t,c),
∵![]() ,
,
∴当![]() 时,y随x
时,y随x![]() 增大而减小,当
增大而减小,当![]() 时,y随x的增大而增大,
时,y随x的增大而增大,
当点![]() ,点
,点![]() ,(2t,c)均在对称轴的右侧时,
,(2t,c)均在对称轴的右侧时,![]() ,
,
∵![]() 1<3,
1<3,
∴2t>3,即![]() (不合题意,舍去),
(不合题意,舍去),
当点![]() 在对称轴的左侧,点
在对称轴的左侧,点![]() ,(2t,c)均在对称轴的右侧时,点
,(2t,c)均在对称轴的右侧时,点![]() 在对称轴的右侧,
在对称轴的右侧,![]() ,
,
此时点![]() 到对称轴
到对称轴![]() 的距离大于点
的距离大于点![]() 到对称轴
到对称轴![]() 的距离,
的距离,
∴![]() ,解得:
,解得:![]() ,
,
∵![]() 1<3,
1<3,
∴2t>3,即![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,对称轴为
,对称轴为![]() ,
,
∴![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() ,
,![]() 的取值范围为
的取值范围为![]() .
.
27. 在![]() 中,
中,![]() ,D为
,D为![]() 内一点,连接
内一点,连接![]() ,
,![]() 延长
延长![]() 到点
到点![]() ,使得
,使得![]()
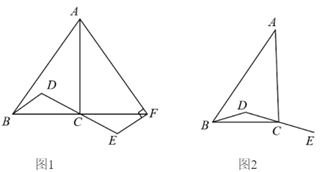
(1)如图1,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() 若
若![]() ,求证:
,求证:![]() ;
;
(2)连接![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,依题意补全图2,若
,依题意补全图2,若![]() ,用等式表示线段
,用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
【参考答案】(1)见解析(2)![]() ;证明见解析
;证明见解析
【小问1详解】
证明:在![]() 和
和![]() 中,
中,
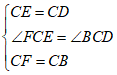 ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵![]() ,
,
∴![]() .
.
【小问2详解】
解:补全后的图形如图所示,![]() ,证明如下:
,证明如下:
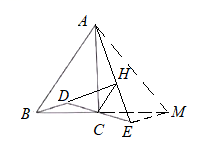
延长BC到点M,使CM=CB,连接EM,AM,
∵![]() ,CM=CB,
,CM=CB,
∴ ![]() 垂直平分BM,
垂直平分BM,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
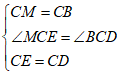 ,
,
∴ ![]() ,
,
∴ ![]() ,
,![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
∴ ![]() ,即
,即![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
28. 在平面直角坐标系![]() 中,已知点
中,已知点![]() 对于点
对于点![]() 给出如下定义:将点
给出如下定义:将点![]() 向右
向右![]() 或向左
或向左![]() 平移
平移![]() 个单位长度,再向上
个单位长度,再向上![]() 或向下
或向下![]() 平移
平移![]() 个单位长度,得到点
个单位长度,得到点![]() ,点
,点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,称点
,称点![]() 为点
为点![]() 的“对应点”.
的“对应点”.
(1)如图,点![]() 点
点![]() 在线段
在线段![]() 的延长线上,若点
的延长线上,若点![]() 点
点![]() 为点
为点![]() 的“对应点”.
的“对应点”.
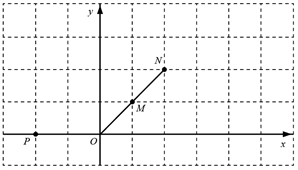
①在图中画出点![]() ;
;
②连接![]() 交线段
交线段![]() 于点
于点![]() 求证:
求证:![]()
(2)![]() 的半径为1,
的半径为1,![]() 是
是![]() 上一点,点
上一点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,若
,若![]() 为
为![]() 外一点,点
外一点,点![]() 为点
为点![]() 的“对应点”,连接
的“对应点”,连接![]() 当点
当点![]() 在
在![]() 上运动时直接写出
上运动时直接写出![]() 长的最大值与最小值的差(用含
长的最大值与最小值的差(用含![]() 的式子表示)
的式子表示)
【参考答案】(1)见解析(2)![]()
【小问1详解】
解:①点Q如下图所示.
∵点![]() ,
,
∴点![]() 向右平移1个单位长度,再向上平移1个单位长度,得到点
向右平移1个单位长度,再向上平移1个单位长度,得到点![]() ,
,
∴![]() ,
,
∵点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,
,![]() ,
,
∴点![]() 的横坐标为:
的横坐标为:![]() ,纵坐标为:
,纵坐标为:![]() ,
,
∴点![]() ,在坐标系内找出该点即可;
,在坐标系内找出该点即可;
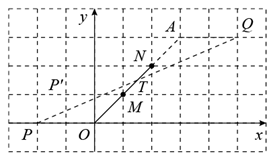
②证明:如图延长ON至点![]() ,连接AQ,
,连接AQ,
∵ ![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
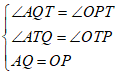 ,
,
∴![]() ,
,
∴![]() ,
,
∵ ![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
【小问2详解】
解:如图所示,
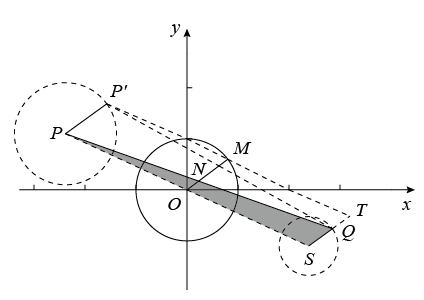
连接PO并延长至S,使![]() ,延长SQ至T,使
,延长SQ至T,使![]() ,
,
∵![]() ,点
,点![]() 向右
向右![]() 或向左
或向左![]() 平移
平移![]() 个单位长度,再向上
个单位长度,再向上![]() 或向下
或向下![]() 平移
平移![]() 个单位长度,得到点
个单位长度,得到点![]() ,
,
∴![]() ,
,
∵点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴OM∥ST,
∴NM为![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
结合题意,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() 长的最大值与最小值的差为
长的最大值与最小值的差为![]()

 三角形内角和定理:三角形三个内角和等于180°,
三角形内角和定理:三角形三个内角和等于180°,