2024年云南中考数学试题及答案解析
一、选择题(本大题共15小题,每小题只有一个正确选项,每小题2分,共30分)
1. 中国是最早使用正负数表示具有相反意义的量的国家.若向北运动100米记作+100米,则向南运动100米可记作( )
A. 100米 B. -100米 C. 200米 D. -200米
【答案】B
【详解】解:若向北运动100米记作+100米,则向南运动100米可记作-100米,
故选:B
2. 某市今年参加初中学业水平考试的学生大约有57800人,57800用科学记数法可以表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【详解】解:![]() ,
,
故选:A.
3. 下列计算正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【详解】解:A、![]() ,选项计算错误,不符合题意;
,选项计算错误,不符合题意;
B、![]() ,选项计算错误,不符合题意;
,选项计算错误,不符合题意;
C、![]() ,选项计算错误,不符合题意;
,选项计算错误,不符合题意;
D、![]() ,选项计算正确,符合题意;
,选项计算正确,符合题意;
故选:D.
4. 式子![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【详解】解:∵式子![]() 在实数范围内有意义,
在实数范围内有意义,
∴![]() 的取值范围是
的取值范围是![]() .
.
故选:B
5. 某图书馆的一个装饰品是由几个几何体组合成的.其中一个几何体的三视图(主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是( )
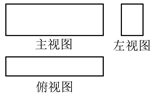
A. 正方体 B. 圆柱 C. 圆锥 D. 长方体
【答案】D
【详解】解:根据三视图的特点:几何体的三视图都是长方形,确定该几何体为长方体.
故选:D.
6. 一个七边形的内角和等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【详解】解:一个七边形的内角和等于![]() ,
,
故选:B.
7. 甲、乙、丙、丁四名运动员参加射击项目选拔赛,每人10次射击成绩的平均数![]() (单位:环)和方差
(单位:环)和方差![]() 如下表所示:
如下表所示:
甲 | 乙 | 丙 | 丁 | |
| 9.9 | 9.5 | 8.2 | 8.5 |
| 0.09 | 0.65 | 0.16 | 2.85 |
根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
【答案】A
【详解】解:由表中数据可知,射击成绩的平均数最大的是甲,射击成绩方差最小的也是甲,
![]() 中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择甲,
中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择甲,
故选:A.
8. 已知为到直线![]() 的距离为3,则点
的距离为3,则点![]() 到直线
到直线![]() 的距离为( )
的距离为( )
A. ![]() B. 2 C. 3 D.
B. 2 C. 3 D. ![]()
【答案】C
【详解】解: 如图,
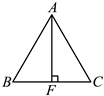
∵![]() 是等腰
是等腰![]() 底边
底边![]() 上的高,
上的高,
∴![]() 平分
平分![]() ,
,
∴点F到直线![]() ,
,![]() 的距离相等,
的距离相等,
∵点![]() 到直线
到直线![]() 的距离为3,
的距离为3,
∴点![]() 到直线
到直线![]() 的距离为3.
的距离为3.
故选:C.
9. 两年前生产1千克甲种药品的成本为80元,随着生产技术的进步,现在生产1千克甲种药品的成本为60元.设甲种药品成本的年平均下降率为![]() ,根据题意,下列方程正确的是( )
,根据题意,下列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【详解】解:![]() 甲种药品成本的年平均下降率为
甲种药品成本的年平均下降率为![]() ,
,
根据题意可得![]() ,
,
故选:B.
10. 按一定规律排列的代数式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,第
,第![]() 个代数式是( )
个代数式是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【详解】解:∵按一定规律排列的代数式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴第![]() 个代数式是
个代数式是![]() ,
,
故选:![]() .
.
11. 中华文明,源远流长;中华汉字,寓意深广.下列四个选项中,是轴对称图形的为( )
A. 爱 B. 国 C. 敬 D. 业
【答案】D
【详解】解:A、图形不是轴对称图形,不符合题意;
B、图形不是轴对称图形,不符合题意;
C、图形不是轴对称图形,不符合题意;
D、图形是轴对称图形,符合题意;
故选:D.
12. 在![]() 中,
中,![]() ,已知
,已知![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【详解】解:∵![]() ,
, ![]() ,
,
∴![]() =
=![]() ,
,
故选:C.
13. 如图,![]() 是
是![]() 的直径,点
的直径,点![]() 、
、![]() 在
在![]() 上.若
上.若![]() ,
,![]() ,则
,则![]() ( )
( )
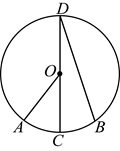
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【详解】解:连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
故选:![]() .
.
14. 分解因式:![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【详解】解:![]()
故选:A.
15. 某校九年级学生参加社会实践,学习编织圆锥型工艺品.若这种圆锥的母线长为![]() 厘米,底面圆的半径为
厘米,底面圆的半径为![]() 厘米,则该圆锥的侧面积为( )
厘米,则该圆锥的侧面积为( )
A. ![]() 平方厘米 B.
平方厘米 B. ![]() 平方厘米
平方厘米
C. ![]() 平方厘米 D.
平方厘米 D. ![]() 平方厘米
平方厘米
【答案】C
【详解】解:圆锥的底面圆周长为![]() 厘米,
厘米,
∴圆锥的侧面积为![]() 平方厘米,
平方厘米,
故选:![]() .
.
二、填空题(本大题共4小题,每小题2分,共8分)
16. 若关于x的一元二次方程![]() 无实数根,则c的取值范围是______.
无实数根,则c的取值范围是______.
【答案】![]() ##
##![]()
【详解】解:根据题意得Δ=(-2)2-4c<0,
解得c>1.
故答案为:c>1.
17. 已知点![]() 在反比例函数
在反比例函数![]() 的图象上,则
的图象上,则![]() __________.
__________.
【答案】![]()
【详解】解:![]() 点
点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
![]() ,
,
故答案为:![]() .
.
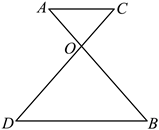
18. 如图,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() .若
.若![]() ,则
,则![]() __________.
__________.
【答案】![]() ##0.5
##0.5
【详解】解:![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
故答案为:![]() .
.
19. 某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用.学校数学兴趣小组为给学校提出合理的采购意见,随机抽取了该校学生![]() 人,了解他们喜欢的体育项目,将收集的数据整理,绘制成如下统计图:
人,了解他们喜欢的体育项目,将收集的数据整理,绘制成如下统计图:
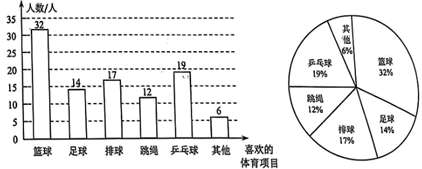
注:该校每位学生被抽到的可能性相等,每位被抽样调查的学生选择且只选择一种喜欢的体育项目.
若该校共有学生![]() 人,则该校喜欢跳绳的学生大约有______人.
人,则该校喜欢跳绳的学生大约有______人.
【答案】![]()
【详解】解:该校喜欢跳绳的学生大约有![]() 人,
人,
故答案为:![]()
三、解答题(本大题共8小题,共62分)
20. 计算:![]() .
.
【答案】![]()
【详解】解:![]() ,
,
![]() ,
,
![]() .
.
21. 如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
求证:![]() .
.

【答案】见解析
【详解】证明:![]()
![]() ,
,
![]()
![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]()
![]() .
.
22. 某旅行社组织游客从![]() 地到
地到![]() 地的航天科技馆参观,已知
地的航天科技馆参观,已知![]() 地到
地到![]() 地的路程为300千米,乘坐
地的路程为300千米,乘坐![]() 型车比乘坐
型车比乘坐![]() 型车少用2小时,
型车少用2小时,![]() 型车的平均速度是
型车的平均速度是![]() 型车的平均速度的3倍,求
型车的平均速度的3倍,求![]() 型车的平均速度.
型车的平均速度.
【答案】![]() 型车的平均速度为
型车的平均速度为![]()
【详解】解:设![]() 型车的平均速度为
型车的平均速度为![]() ,则
,则![]() 型车的平均速度是
型车的平均速度是![]() ,
,
根据题意可得,![]() ,
,
整理得,![]() ,
,
解得![]() ,
,
经检验![]() 是该方程的解,
是该方程的解,
答:![]() 型车的平均速度为
型车的平均速度为![]() .
.
23. 为使学生更加了解云南,热爱家乡,热爱祖国,体验“有一种叫云南的生活”.某校七年级年级组准备从博物馆![]() 、植物园
、植物园![]() 两个研学基地中,随机选择一个基地研学,且每个基地被选到的可能性相等;八年级年级组准备从博物馆
两个研学基地中,随机选择一个基地研学,且每个基地被选到的可能性相等;八年级年级组准备从博物馆![]() 、植物园
、植物园![]() 、科技馆
、科技馆![]() 三个研学基地中,随机选择一个基地研学,且每个基地被选到的可能性相等.记选择博物馆
三个研学基地中,随机选择一个基地研学,且每个基地被选到的可能性相等.记选择博物馆![]() 为
为![]() ,选择植物园
,选择植物园![]() 为
为![]() ,选择科技馆
,选择科技馆![]() 为
为![]() ,记七年级年级组的选择为
,记七年级年级组的选择为![]() ,八年级年级组的选择为
,八年级年级组的选择为![]() .
.
(1)请用列表法或画树状图法中的一种方法,求![]() 所有可能出现的结果总数;
所有可能出现的结果总数;
(2)求该校七年级年级组、八年级年级组选择的研学基地互不相同的概率![]() .
.
【答案】(1)见解析 (2)![]()
【解析】
【分析】本题考查利用列表法或画树状图求概率,解题的关键在于根据题意列表或画树状图.
(1)根据题意列出表格(或画出树状图)即可解题;
(2)根据概率![]() 所求情况数与总情况数之比.由表格(或树状图),得到共有6个等可能的结果,该校七年级年级组、八年级年级组选择的研学基地互不相同的情况有
所求情况数与总情况数之比.由表格(或树状图),得到共有6个等可能的结果,该校七年级年级组、八年级年级组选择的研学基地互不相同的情况有![]() 种,再由概率公式求解即可.
种,再由概率公式求解即可.
【小问1详解】
解:由题意可列表如下:
| | |
| | |
| | |
| | |
由表格可知,![]()
【小问2详解】
解:由表格可知,该校七年级年级组、八年级年级组选择的研学基地互不相同的情况
![]()
24. 如图,在四边形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是各边的中点,且
分别是各边的中点,且![]() ,
,![]() ,四边形
,四边形![]() 是矩形.
是矩形.
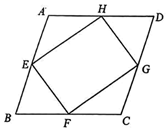
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若矩形![]() 的周长为22,四边形
的周长为22,四边形![]() 的面积为10,求
的面积为10,求![]() 的长.
的长.
【答案】(1)见解析 (2)![]()
【解析】
【小问1详解】
解:连接![]() ,
,![]() ,
,
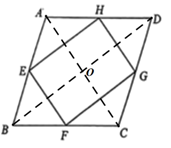
![]()
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 四边形
四边形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是各边的中点,
分别是各边的中点,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]()
![]() ,
,
![]() 四边形
四边形![]() 是菱形;
是菱形;
【小问2详解】
解:![]() 四边形
四边形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是各边的中点,
分别是各边的中点,
![]() ,
,![]() ,
,
![]() 矩形
矩形![]() 的周长为22,
的周长为22,
![]()
![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,
即![]() ,
,
![]() 四边形
四边形![]() 的面积为10,
的面积为10,
![]() ,即
,即![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
25. ![]() 、
、![]() 两种型号的吉祥物具有吉祥如意、平安幸福的美好寓意,深受大家喜欢.
两种型号的吉祥物具有吉祥如意、平安幸福的美好寓意,深受大家喜欢.
某超市销售![]() 、
、![]() 两种型号的吉祥物,有关信息见下表:
两种型号的吉祥物,有关信息见下表:
成本(单位:元/个) | 销售价格(单位:元/个) | |
| 35 | a |
| 42 | |
若顾客在该超市购买8个![]() 种型号吉祥物和7个
种型号吉祥物和7个![]() 种型号吉祥物,则一共需要670元;购买4个
种型号吉祥物,则一共需要670元;购买4个![]() 种型号吉祥物和5个
种型号吉祥物和5个![]() 种型号吉祥物,则一共需要410元.
种型号吉祥物,则一共需要410元.
(1)求![]() 、
、![]() 的值;
的值;
(2)若某公司计划从该超市购买![]() 、
、![]() 两种型号的吉祥物共90个,且购买
两种型号的吉祥物共90个,且购买![]() 种型号吉祥物的数量
种型号吉祥物的数量![]() (单位:个)不少于
(单位:个)不少于![]() 种型号吉祥物数量的
种型号吉祥物数量的![]() ,又不超过
,又不超过![]() 种型号吉祥物数量的2倍.设该超市销售这90个吉祥物获得的总利润为
种型号吉祥物数量的2倍.设该超市销售这90个吉祥物获得的总利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
注:该超市销售每个吉祥物获得的利润等于每个吉祥物的销售价格与每个吉祥物的成本的差.
?D. ![]()
(2)![]()
【解析】
【小问1详解】
解:由题知,![]() ,
,
解得![]() ;
;
【小问2详解】
解:![]() 购买
购买![]() 种型号吉祥物的数量
种型号吉祥物的数量![]() 个,
个,
则购买![]() 种型号吉祥物的数量
种型号吉祥物的数量![]() 个,
个,
![]() 且购买
且购买![]() 种型号吉祥物的数量
种型号吉祥物的数量![]() (单位:个)不少于
(单位:个)不少于![]() 种型号吉祥物数量的
种型号吉祥物数量的![]() ,
,
![]()
![]() ,
,
解得![]() ,
,
![]()
![]() 种型号吉祥物的数量又不超过种型号吉祥物数量的2倍.
种型号吉祥物的数量又不超过种型号吉祥物数量的2倍.
![]()
![]() ,
,
解得![]() ,
,
即![]() ,
,
由题知,![]() ,
,
整理得![]() ,
,
![]()
![]() 随
随![]() 的增大而减小,
的增大而减小,
![]() 当
当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
26. 已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() .设
.设![]() 是抛物线
是抛物线![]() 与
与![]() 轴交点的横坐标,记
轴交点的横坐标,记![]() .
.
(1)求![]() 的值;
的值;
(2)比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)![]()
(2)当![]() 时,
时,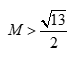 ;当
;当![]() 时,
时, ![]() .
.
【解析】
【小问1详解】
解:∵抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,
,
∴![]() ,
,
∴![]() ;
;
【小问2详解】
解:∵![]() 是抛物线
是抛物线![]() 与
与![]() 轴交点的横坐标,
轴交点的横坐标,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
而![]()
代入得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
解得:![]() ,
,
当![]() 时,
时,![]()
∴![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() .
.
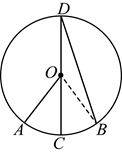
27. 如图,![]() 是为是为在直径
是为是为在直径![]() 上,
上,![]() ,点
,点![]() 是线段
是线段![]() 的中点
的中点

(1)求![]() 的度数;
的度数;
(2)求证:直线![]() 与
与![]() 相切:
相切:
(3)看一看,想一想,证一证:
以下与线段![]() 、线段
、线段![]() 、线段
、线段![]() 有关的三个结论:
有关的三个结论:![]() ,
,![]() ,
,![]() ,你认为哪个正确?请说明理由.
,你认为哪个正确?请说明理由.
【答案】(1)![]()
(2)见解析 (3)![]() ,理由见解析
,理由见解析
【小问1详解】
解:∵![]() 是为是
是为是![]() 上异于
上异于![]() 、
、![]() 的点,
的点,
∴![]() ;
;
【小问2详解】
证明:∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是半径,
是半径,
∴直线![]() 与
与![]() 相切;
相切;
【小问3详解】
我认为:![]() 正确,理由如下:
正确,理由如下:
连接![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,如图,则:
,如图,则:![]() ,
,
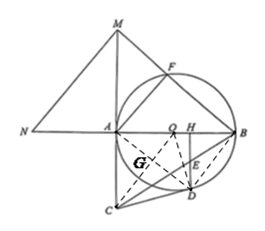
∴点![]() 在线段
在线段![]() 的中垂线上,
的中垂线上,
∵![]() ,
,
∴点![]() 在线段
在线段![]() 的中垂线上,
的中垂线上,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 三点共线,
三点共线,
∴![]() .
.
