2022年成人高考专升本高等数学(二)真题及答案

2022年成人高考专升本高等数学(二)真题及答案

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分150分.考试时间150分钟.

第Ⅰ卷（选择题，共40分）

一、选择题（1～10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.设函数则（      ）

A．是奇函数但不是周期函数  

B．是偶函数但不是周期函数

C．既是奇函数又是周期函数        

D. 既是偶函数又是周期函数

2. 若，则（      ）

A. 1         B. 2         C. 3        D. 4

3.设函数在处连续，在处不连续，则在处（      ） 

  A. 连续           B. 不连续     

 C. 连续           D. 不连续

4. 设，则（      ）

  A.        B.         C.       D.

5.设，则（      ）

A.           B.           C.      D.

6.设，则（      ）

A.         B.       C.    D.

7.若函数的导数，则（      ）

A. 在单调递减

B. 在单调递增

C. 在单调递增

D. 在单调递增

8.曲线的水平渐近线方程为（      ）

A.        B.       C.        D.

9.设函数，则（      ）

A.        B.

C.         D.

10.设，则 (      ）                                   

A.        B.      C.        D.

第II卷（非选择题，共110分）

二、填空题（11-20小题，每题4分，共40分）

11.             

12.当 时，函数是的高阶无穷小量，则            .

13. 设，则           .

14.曲线在点（1，2）处的法线方程为            .

15.            .

16.            .

17. 设函数，则           .

18.设则           .

19.设函数具有连续偏导数，则         .

20.设A，B为两个随机事件，且则          .

三、解答题（21-28题，共70分。解答应写出推理、演算步骤）

21.计算（本题满分8分）

设函数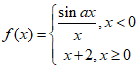在处连续，求.

22.（本题满分8分）

设，求

23. （本题满分8分）

   求

24. （本题满分8分）

     计算

25. （本题满分8分）

设离散型随机变量的概率分布为

(1)求的分布函数，

(2)求.

26. （本题满分10分）

设是由方程所确定的隐函数，求

27. （本题满分10分）

设D为由曲线所围成的图形.

(1)求D的面积.

(2)求D绕轴旋转一周所得旋转体的体积.   

28. （本题满分10分）

证明：当时，.

参考答案和解析

一、选择题

1.【答案】B

【考情点拨】本题考查了复合函数的性质的知识点.

【应试指导】而，所以函数是偶函数，但不是周期函数。

2.【答案】A

【考情点拨】本题考查了洛比达法则的知识点.

【应试指导】故.

3.【答案】D

【考情点拨】本题考查了函数的连续性的知识点.

【应试指导】在处连续，在处连续，故在处不连续.否则若在处连续，则在处连续，与题意矛盾，故选D选项。

4.【答案】B

【考情点拨】本题考查了函数导数的知识点.

【应试指导】.

5.【答案】B

【考情点拨】本题考查了复合函数的导数的知识点.

【应试指导】.

6.【答案】A

【考情点拨】本题考查了高阶导数的知识点.

【应试指导】.所以

7.【答案】C

【考情点拨】本题考查了函数的单调性的知识点.

【应试指导】当时此，，故函数的单调递增区间为；当时，，故函数的单调递减区间为。因此选C选项。

8.【答案】C

【考情点拨】本题考查了函数的水平渐近线的知识点.

【应试指导】由于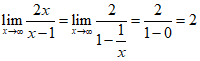.故函数的水平渐近线为.

9.【答案】A

【考情点拨】本题考查了不定积分的性质的知识点.

【应试指导】.

10.【答案】D

【考情点拨】本题考查了二阶函数的全微分的知识点.

【应试指导】由题可得.故，因此.

二、解答题

11.【答案】-1

【考情点拨】本题考查了洛比达法则的知识点.

【应试指导】.

12.【答案】0

【考情点拨】本题考查了高阶无穷小的知识点.

【应试指导】当时，是的高阶无穷小量，故

13.【答案】

【考情点拨】本题考查了导数的性质的知识点.

【应试指导】.

14.【答案】

【考情点拨】本题考查了导数的几何意义的知识点.

【应试指导】由题可得故，因此曲线在点（1，2）处法线的斜率是，故所求法线的方程为即.

15.【答案】

【考情点拨】本题考查了对称区间上奇偶函数的定积分的性质的知识点.

【应试指导】令，因此为奇函数，所以.

16.【答案】

【考情点拨】本题考查了定积分的计算的知识点.

【应试指导】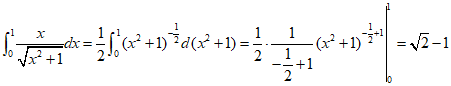 

17.【答案】

【考情点拨】本题考查了变上限定积分的知识点.

【应试指导】由题意可得.因此

18.【答案】

【考情点拨】本题考查了二阶偏导数的知识点.

【应试指导】.

19.【答案】

【考情点拨】本题考查了复合函数的偏导数的知识点.

【应试指导】.

20.【答案】

【考情点拨】本题考查了条件概率的知识点.

【应试指导】.

三、解答题

21. 因为在处连续，所以

由于，所以.

22. .

23.

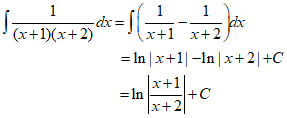
24.

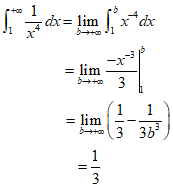
25.(1) ，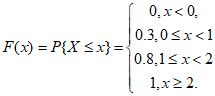

 (2)

26.方程两边分别对和求偏导数得

.

解得

27.

(1)D的面积

(2)D绕轴旋转一周所得旋转体的体积

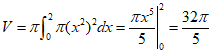
28.设，则

当时，，故在单调递增.

又因为在处连续，且，所以当时，.

因此当时，即