2023年贵州中考数学试题及答案
同学你好!答题前请认真阅读以下内容:
1.全卷共6页,三个大题,共25题,满分150分.考试时间为120分钟.考试形式闭卷.
2.一律在答题卡相应位置作答,在试题卷上答题视为无效.
3.不能使用计算器.
一、选择题(每小题3分,共36分.每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置填涂)
1.5的绝对值是( )
A.![]() B.5 C.
B.5 C.![]() D.
D.![]()
2.如图所示的几何体,从正面看,得到的平面图形是( )
A. B.
B. C.
C. D.
D.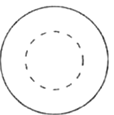
3.据中国经济网资料显示,今年一季度全国居民人均可支配收入平稳增长,全国居民人均可支配收入为10870元.10870这个数用科学记数法表示正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,![]() 与
与![]() 相交于点
相交于点![]() .若
.若![]() ,则
,则![]() 的度数是( )
的度数是( )
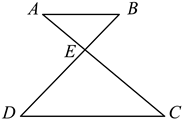
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.化简![]() 结果正确的是( )
结果正确的是( )
A.1 B.![]() C.
C.![]() D.
D.![]()
6.“石阡苔茶”是贵州十大名茶之一,在我国传统节日清明节前后,某茶叶经销商对甲、乙、丙、丁四种包装的苔茶(售价、利润均相同)在一段时间内的销售情况统计如下表,最终决定增加乙种包装苔茶的进货数量,影响经销商决策的统计量是( )
包装 | 甲 | 乙 | 丙 | 丁 |
销售量(盒) |
|
|
|
|
A.中位数 B.平均数 C.众数 D.方差
7.5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为![]() ,腰长为
,腰长为![]() ,则底边上的高是( )
,则底边上的高是( )
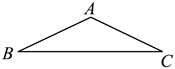
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.在学校科技宣传活动中,某科技活动小组将3个标有“北斗”,2个标有“天眼”,5个标有“高铁”的小球(除标记外其它都相同)放入盒中,小红从盒中随机摸出1个小球,并对小球标记的内容进行介绍,下列叙述正确的是( )
A.模出“北斗”小球的可能性最大 B.摸出“天眼”小球的可能性最大
C.摸出“高铁”小球的可能性最大 D.摸出三种小球的可能性相同
9.《孙子算经》中有这样一道题,大意为:今有100头鹿,每户分一头鹿后,还有剩余,将剩下的鹿按每3户共分一头,恰好分完,问:有多少户人家?若设有x户人家,则下列方程正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知,二次数![]() 的图象如图所示,则点
的图象如图所示,则点![]() 所在的象限是( )
所在的象限是( )
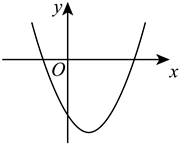
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .按下列步骤作图:①以
.按下列步骤作图:①以
点D为圆心,适当长度为半径画弧,分别交![]() 于E,F两点;②分别以点E,F为圆心以大于
于E,F两点;②分别以点E,F为圆心以大于![]() 的长为半径画弧,两弧交于点P;③连接
的长为半径画弧,两弧交于点P;③连接![]() 并延长交
并延长交![]() 于点G.则
于点G.则![]() 的长是( )
的长是( )
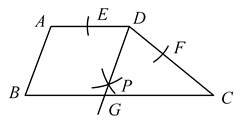
A.2 B.3 C.4 D.5
12.今年“五一”假期,小星一家驾车前往黄果树旅游,在行驶过程中,汽车离黄果树景点的路程y(![]() )与所用时间x(h)之间的函数关系的图象如图所示,下列说法正确的是( )
)与所用时间x(h)之间的函数关系的图象如图所示,下列说法正确的是( )
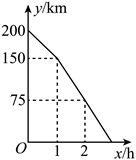
A.小星家离黄果树景点的路程为![]() B.小星从家出发第1小时的平均速度为
B.小星从家出发第1小时的平均速度为![]()
C.小星从家出发2小时离景点的路程为![]() D.小星从家到黄果树景点的时间共用了
D.小星从家到黄果树景点的时间共用了![]()
二、填空题(每小题4分,共16分)
13.因式分解:![]() __________.
__________.
14.如图,是贵阳市城市轨道交通运营部分示意图,以喷水池为原点,分别以正东、正北方向为![]() 轴、
轴、![]() 轴的正方向建立平面直角坐标系,若贵阳北站的坐标是
轴的正方向建立平面直角坐标系,若贵阳北站的坐标是![]() ,则龙洞堡机场的坐标是_______.
,则龙洞堡机场的坐标是_______.

15.若一元二次方程![]() 有两个相等的实数根,则
有两个相等的实数根,则![]() 的值是_______.
的值是_______.
16.如图,在矩形![]() 中,点
中,点![]() 为矩形内一点,且
为矩形内一点,且![]() ,
,![]() ,则四边形
,则四边形![]() 的面积是_______.
的面积是_______.
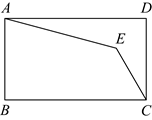
三、解答题(本大题共9题,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(1)计算:![]() ;
;
(2)已知,![]() .若
.若![]() ,求
,求![]() 的取值范围.
的取值范围.
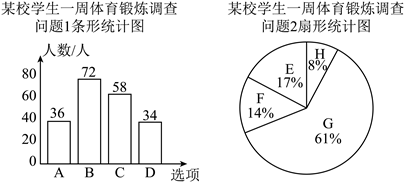
18.为加强体育锻炼,某校体育兴趣小组,随机抽取部分学生,对他们在一周内体育锻炼的情况进行问卷调查,根据问卷结果,绘制成如下统计图.请根据相关信息,解答下列问题:
某校学生一周体育锻炼调查问卷 以下问题均为单选题,请根据实际情况填写(其中0~4表示大于等于0同时小于4) 问题:你平均每周体育锻炼的时间大约是( ) A.0~4小时 B.4~6小时 C.6~8小时 D.8~小时及以上 问题2:你体育镀炼的动力是( ) E.家长要求 F.学校要求 G.自己主动 H.其他 |
|
(1)参与本次调查的学生共有_______人,选择“自己主动”体育锻炼的学生有_______人;
(2)已知该校有2600名学生,若每周体育锻炼8小时以上(含8小时)可评为“运动之星”,请估计全校可评为“运动之星”的人数;
(3)请写出一条你对同学体育锻炼的建议.
19.为推动乡村振兴,政府大力扶持小型企业.根据市场需求,某小型企业为加快生产速度,需要更新生产设备,更新设备后生产效率比更新前提高了![]() ,设更新设备前每天生产x件产品.解答下列问题:
,设更新设备前每天生产x件产品.解答下列问题:
(1)更新设备后每天生产_______件产品(用含x的式子表示);
(2)更新设备前生产5000件产品比更新设备后生产6000件产品多用2天,求更新设备后每天生产多少件产品.
20.如图,在![]() 中,
中,![]() ,延长
,延长![]() 至D,使得
至D,使得![]() ,过点A,D分别作
,过点A,D分别作![]() ,
,![]() ,
,![]() 与
与![]() 相交于点E.下面是两位同学的对话:
相交于点E.下面是两位同学的对话:
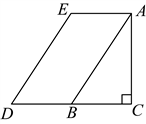
| 小星:由题目的已知条件,若连接 证明 | 小红:由题目的已知条件,若连接 |
|
(1)请你选择一位同学的说法,并进行证明;
(2)连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
21.如图,在平面直角坐标系中,四边形![]() 是矩形,反比例函数
是矩形,反比例函数![]() 的图象分别与
的图象分别与![]() 交于点
交于点![]() 和点
和点![]() ,且点
,且点![]() 为
为![]() 的中点.
的中点.
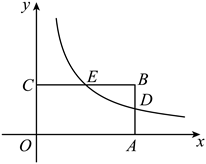
(1)求反比例函数的表达式和点![]() 的坐标;
的坐标;
(2)若一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,当点
,当点![]() 在反比例函数图象上
在反比例函数图象上![]() 之间的部分时(点
之间的部分时(点![]() 可与点
可与点![]() 重合),直接写出
重合),直接写出![]() 的取值范围.
的取值范围.
22.贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚![]() 为起点,沿途修建
为起点,沿途修建![]() 、
、![]() 两段长度相等的观光索道,最终到达山顶
两段长度相等的观光索道,最终到达山顶![]() 处,中途设计了一段与
处,中途设计了一段与![]() 平行的观光平台
平行的观光平台![]() 为
为![]() .索道
.索道![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 与水平线夹角为
与水平线夹角为![]() ,
,![]() 两处的水平距离
两处的水平距离![]() 为
为![]() ,
,![]() ,垂足为点
,垂足为点![]() .(图中所有点都在同一平面内,点
.(图中所有点都在同一平面内,点![]() 在同一水平线上)
在同一水平线上)
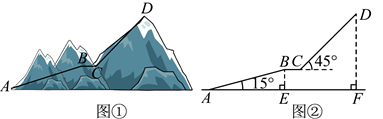
(1)求索道![]() 的长(结果精确到
的长(结果精确到![]() );
);
(2)求水平距离![]() 的长(结果精确到
的长(结果精确到![]() ).
).
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
23.如图,已知![]() 是等边三角形
是等边三角形![]() 的外接圆,连接
的外接圆,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
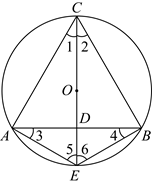
(1)写出图中一个度数为![]() 的角:_______,图中与
的角:_______,图中与![]() 全等的三角形是_______;
全等的三角形是_______;
(2)求证:![]() ;
;
(3)连接![]() ,
,![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
24.如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在![]() 处,对称轴
处,对称轴![]() 与水平线
与水平线![]() 垂直,
垂直,![]() ,点
,点![]() 在抛物线上,且点
在抛物线上,且点![]() 到对称轴的距离
到对称轴的距离![]() ,点
,点![]() 在抛物线上,点
在抛物线上,点![]() 到对称轴的距离是1.
到对称轴的距离是1.
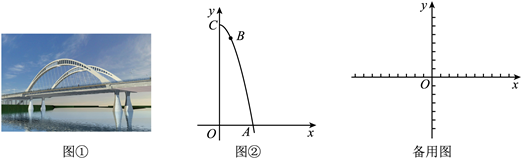
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在![]() 上找一点
上找一点![]() ,加装拉杆
,加装拉杆![]() ,同时使拉杆的长度之和最短,请你帮小星找到点
,同时使拉杆的长度之和最短,请你帮小星找到点![]() 的位置并求出坐标;
的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为![]() ,当
,当![]() 时,函数
时,函数![]() 的值总大于等于9.求
的值总大于等于9.求![]() 的取值范围.
的取值范围.
25.如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形![]() 中,
中,![]() ,过点
,过点![]() 作射线
作射线![]() ,垂足为
,垂足为![]() ,点
,点![]() 在
在![]() 上.
上.
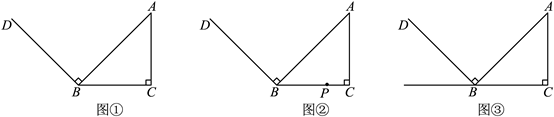
(1)【动手操作】
如图②,若点![]() 在线段
在线段![]() 上,画出射线
上,画出射线![]() ,并将射线
,并将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 与
与![]() 交于点
交于点![]() ,根据题意在图中画出图形,图中
,根据题意在图中画出图形,图中![]() 的度数为_______度;
的度数为_______度;
(2)【问题探究】
根据(1)所画图形,探究线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)【拓展延伸】
如图③,若点![]() 在射线
在射线![]() 上移动,将射线
上移动,将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 与
与![]() 交于点
交于点![]() ,探究线段
,探究线段![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
参考答案
1.B
2.A
3.B
4.B
5.A
6.C
7.B
8.C
9.C
10.D
11.A
12.D
13.![]()
14.![]()
15.![]()
16.![]()
17.(1)4;(2)![]()
18.(1)200,122
(2)442人
(3)解:体育锻炼是强身健体的一个非常好的途径,只有有一个良好的身体状况,才能更好的把自己的精力投入到学习中,因此建议学生多多主动加强每周的体育锻炼时间.
19.(1)![]()
(2)125件
20.(1)见解析
(2)![]()
21.(1)反比例函数解析式为![]() ,
,![]()
(2)![]()
22.(1)![]()
(2)![]()
23.(1)![]() 、
、![]() 、
、![]() 、
、![]() ;
;![]() ;
;
(2)证明见详解;
(3)四边形![]() 是菱形;
是菱形;
24.(1)![]()
(2)点![]() 的坐标为
的坐标为![]()
(3)![]()
25.(1) 135
(2)![]() ;理由见解析
;理由见解析
(3)![]() 或
或![]() ;
;