2023年甘肃兰州中考数学真题及答案
一、选择题(本大题共12小题,每小题3分,共36分)
1. -5的相反数是( )
A. ![]() B.
B. ![]() C. 5 D. -5
C. 5 D. -5
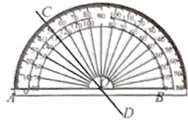
2. 如图,直线![]() 与
与![]() 相交于点O,则
相交于点O,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 计算:![]() ( )
( )
A. ![]() B.
B. ![]() C. 5 D. a
C. 5 D. a
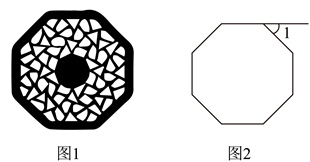
4. 如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图2是八角形空窗的示意图,它的一个外角![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 方程![]() 的解是( )
的解是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
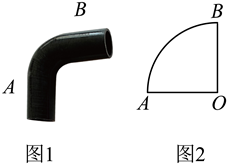
6. 如图1是一段弯管,弯管的部分外轮廓线如图2所示是一条圆弧![]() ,圆弧的半径
,圆弧的半径![]() ,圆心角
,圆心角![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 已知二次函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 对称轴为![]() B. 顶点坐标为
B. 顶点坐标为![]() C. 函数的最大值是-3 D. 函数的最小值是-3
C. 函数的最大值是-3 D. 函数的最小值是-3
8. 关于x的一元二次方程![]() 有两个相等的实数根,则
有两个相等的实数根,则![]() ( )
( )
A -2 B. 2 C. -4 D. 4
9. 2022年我国新能源汽车销量持续增长,全年销量约为572.6万辆,同比增长91.7%,连续8年位居全球第一.下面的统计图反映了2021年、2022年新能源汽车月度销量及同比增长速度的情况.(2022年同比增长速度![]() )根据统计图提供的信息,下列推断不合理的是( )
)根据统计图提供的信息,下列推断不合理的是( )
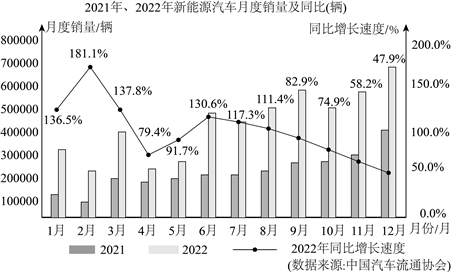
A. 2021年新能源汽车月度销量最高是12月份,超过40万辆
B. 2022年新能源汽车月度销量超过50万辆的月份有6个
C. 相对于2021年,2022年新能源汽车同比增长速度最快的是2月份,达到了181.1%
D. 相对于2021年,2022年从5月份开始新能源汽车同比增长速度持续降低
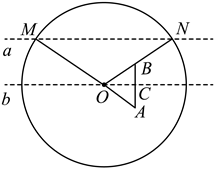
10. 我国古代天文学确定方向的方法中蕴藏了平行线的作图法.如《淮南子天文训》中记载:“正朝夕:先树一表东方;操一表却去前表十步,以参望日始出北廉.日直入,又树一表于东方,因西方之表,以参望日方入北康.则定东方两表之中与西方之表,则东西也.”如图,用几何语言叙述作图方法:已知直线a和直线外一定点O,过点O作直线与a平行.(1)以O为圆心,单位长为半径作圆,交直线a于点M,N;(2)分别在![]() 的延长线及
的延长线及![]() 上取点A,B,使
上取点A,B,使![]() ;(3)连接
;(3)连接![]() ,取其中点C,过O,C两点确定直线b,则直线
,取其中点C,过O,C两点确定直线b,则直线![]() .按以上作图顺序,若
.按以上作图顺序,若![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
11. 一次函数![]() 的函数值y随x的增大而减小,当
的函数值y随x的增大而减小,当![]() 时,y的值可以是( )
时,y的值可以是( )
A. 2 B. 1 C. -1 D. -2
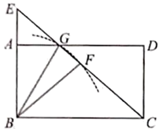
12. 如图,在矩形![]() 中,点E为
中,点E为![]() 延长线上一点,F为
延长线上一点,F为![]() 的中点,以B为圆心,
的中点,以B为圆心,![]() 长为半径的圆弧过
长为半径的圆弧过![]() 与
与![]() 的交点G,连接
的交点G,连接![]() .若
.若![]() ,
,![]() ,则
,则![]() ( )
( )
A. 2 B. 2.5 C. 3 D. 3.5
二、填空题(本大题共4小题,每小题3分,共12分)
13. 因式分解:![]() ______.
______.
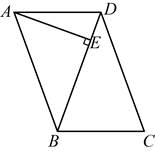
14. 如图,在![]() 中,
中,![]() ,
,![]() 于点E,若
于点E,若![]() ,则
,则![]() ______
______![]() .
.
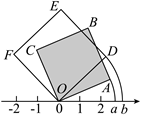
15. 如图,将面积为7的正方形![]() 和面积为9的正方形
和面积为9的正方形![]() 分别绕原点O顺时针旋转,使
分别绕原点O顺时针旋转,使![]() ,
,![]() 落在数轴上,点A,D在数轴上对应的数字分别为a,b,则
落在数轴上,点A,D在数轴上对应的数字分别为a,b,则![]() ______.
______.
16. 某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如下表:
累计抛掷次数 | 50 | 100 | 200 | 300 | 500 | 1000 | 2000 | 3000 | 5000 |
盖面朝上次数 | 28 | 54 | 106 | 158 | 264 | 527 | 1056 | 1587 | 2850 |
盖面朝上频率 |
|
|
|
|
|
|
|
|
|
下面有三个推断:
①通过上述实验的结果,可以推断这枚瓶盖有很大的可能性不是质地均匀的;
②第2000次实验的结果一定是“盖面朝上”;
③随着实验次数的增大,“盖面朝上”的概率接近0.53.
其中正确的是______.(填序号)
三、解答题(本大题共12小题,共72分)
17. 计算:![]() .
.
18. 计算:![]() .
.
19. 解不等式组: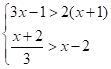 .
.
20. 如图,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() ,
,![]() 轴于点D,分别交反比例函数与一次函数的图象于点B,C.
轴于点D,分别交反比例函数与一次函数的图象于点B,C.
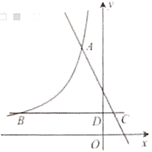
(1)求反比例函数![]() 与一次函数
与一次函数![]() 的表达式;
的表达式;
(2)当![]() 时,求线段
时,求线段![]() 的长.
的长.
21. 综合与实践
问题探究:(1)如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在![]() 和
和![]() 上分别取点C和D,使得
上分别取点C和D,使得![]() ,连接
,连接![]() ,以
,以![]() 为边作等边三角形
为边作等边三角形![]() ,则
,则![]() 就是
就是![]() 的平分线.
的平分线.
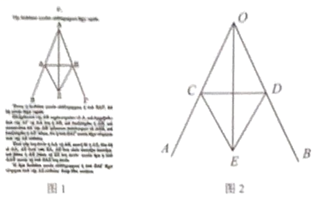
请写出![]() 平分
平分![]() 的依据:____________;
的依据:____________;
类比迁移:
(2)小明根据以上信息研究发现:![]() 不一定必须是等边三角形,只需
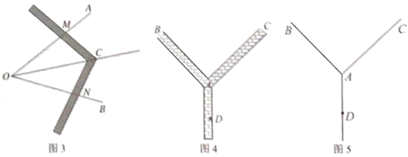
不一定必须是等边三角形,只需![]() 即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在
即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在![]() 的边
的边![]() ,
,![]() 上分别取
上分别取![]() ,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线
,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线![]() 是
是![]() 的平分线,请说明此做法的理由;
的平分线,请说明此做法的理由;
拓展实践:
(3)小明将研究应用于实践.如图4,校园的两条小路![]() 和
和![]() ,汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
,汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
22. 如图1是我国第一个以“龙”为主题的主题公园——“兰州龙源”.“兰州龙源”的“龙”字主题雕塑以紫铜铸造,如巨龙腾空,气势如虹,屹立在黄河北岸.某数学兴趣小组开展了测量“龙”字雕塑CD高度的实践活动.具体过程如下:如图2,“龙”字雕塑CD位于垂直地面的基座BC上,在平行于水平地面的A处测得![]() 、
、![]() ,
,![]() .求“龙”字雕塑
.求“龙”字雕塑![]() 的高度.(B,C,D三点共线,
的高度.(B,C,D三点共线,![]() .结果精确到0.1m)(参考数据:
.结果精确到0.1m)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

23. 一名运动员在![]() 高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面
高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面![]() 的高度
的高度![]() 与离起跳点A的水平距离
与离起跳点A的水平距离![]() 之间的函数关系如图所示,运动员离起跳点A的水平距离为
之间的函数关系如图所示,运动员离起跳点A的水平距离为![]() 时达到最高点,当运动员离起跳点A的水平距离为
时达到最高点,当运动员离起跳点A的水平距离为![]() 时离水面的距离为
时离水面的距离为![]() .
.
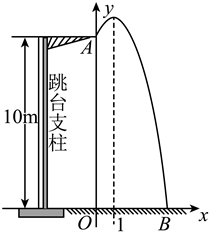
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离![]() 的长.
的长.
24. 如图,矩形![]() 的对角线
的对角线![]() 与
与![]() 相交于点O,
相交于点O,![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 分别交
分别交![]() 于点F,G,连接
于点F,G,连接![]() .
.
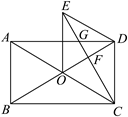
(1)判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)当![]() 时,求
时,求![]() 的长.
的长.
25. 某校八年级共有男生300人,为了解该年级男生排球垫球成绩和掷实心球成绩的情况,从中随机抽取40名男生进行测试,对数据进行整理、描述和分析,下面是给出的部分信息.
信息一:排球垫球成绩如下图所示(成绩用x表示,分成六组:A. ![]() ;B.
;B. ![]() ;C.
;C. ![]() ;D.
;D. ![]() ;E.
;E. ![]() ;F.
;F. ![]() ).
).
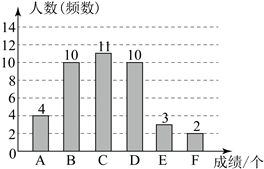
信息二:排球垫球成绩在D. ![]() 这一组的是:
这一组的是:
20,20,21,21,21,22,22,23,24,24
信息三:掷实心球成绩(成绩用y表示,单位:米)的人数(频数)分布表如下:
分组 |
|
|
|
|
|
|
人数 | 2 | m | 10 | 9 | 6 | 2 |
信息四:这次抽样测试中6名男生的两项成绩的部分数据如下:
学生 | 学生1 | 学生2 | 学生3 | 学生4 | 学生5 | 学生6 |
排球垫球 | 26 | 25 | 23 | 22 | 22 | 15 |
掷实心球 | ▲ | 7.8 | 7.8 | ▲ | 8.8 | 9.2 |
根据以上信息,回答下列问题:
(1)填空:![]() ______;
______;
(2)下列结论正确的是_____;(填序号)
①排球垫球成绩超过10个的人数占抽取人数的百分比低于60%;
②掷实心球成绩的中位数记为n,则![]() ;
;
③若排球垫球成绩达到22个及以上时,成绩记为优秀.如果信息四中6名男生的两项成绩恰好为优秀的有4名,那么学生3掷实心球的成绩是优秀.
(3)若排球垫球成绩达到22个及以上时,成绩记为优秀,请估计全年级男生排球垫球成绩达到优秀的人数.
26. 如图,![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() .
.
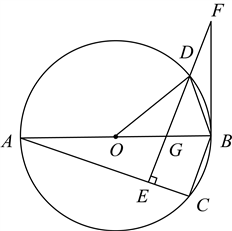
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)当![]() 时,求
时,求![]() 的长.
的长.
27. 在平面直角坐标系中,给出如下定义:![]() 为图形
为图形![]() 上任意一点,如果点
上任意一点,如果点![]() 到直线
到直线![]() 的距离等于图形
的距离等于图形![]() 上任意两点距离的最大值时,那么点
上任意两点距离的最大值时,那么点![]() 称为直线
称为直线![]() 的“伴随点”.
的“伴随点”.
例如:如图1,已知点![]() ,
,![]() ,
,![]() 在线段
在线段![]() 上,则点
上,则点![]() 是直线
是直线![]() :
:![]() 轴的“伴随点”.
轴的“伴随点”.
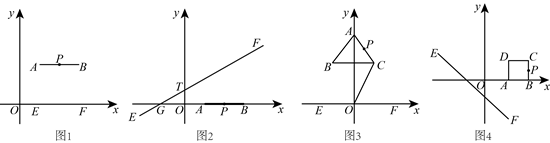
(1)如图2,已知点![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点,直线
上一点,直线![]() 过
过![]() ,
,
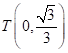 两点,当点
两点,当点![]() 是直线
是直线![]() 的“伴随点”时,求点
的“伴随点”时,求点![]() 的坐标;
的坐标;
(2)如图3,![]() 轴上方有一等边三角形
轴上方有一等边三角形![]() ,
,![]() 轴,顶点
轴,顶点![]() 在
在![]() 轴上且在
轴上且在![]() 上方,
上方,![]() ,点
,点![]() 是
是![]() 上一点,且点
上一点,且点![]() 是直线
是直线![]() :
:![]() 轴的
轴的![]() 伴随点
伴随点![]() .当点
.当点![]() 到
到![]() 轴的距离最小时,求等边三角形
轴的距离最小时,求等边三角形![]() 的边长;
的边长;
(3)如图4,以![]() ,
,![]() ,
,![]() 为顶点的正方形
为顶点的正方形![]() 上始终存在点
上始终存在点![]() ,使得点
,使得点![]() 是直线
是直线![]() :
:![]() 的
的![]() 伴随点
伴随点![]() .请直接写出
.请直接写出![]() 的取值范围.
的取值范围.
28.
综合与实践
【思考尝试】
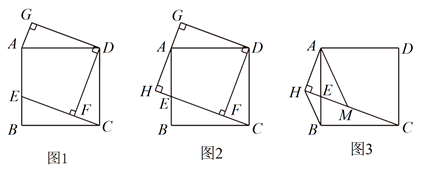
(1)数学活动课上,老师出示了一个问题:如图1,在矩形ABCD中,E是边![]() 上一点,
上一点,![]() 于点F,
于点F,![]() ,
,![]() ,
,![]() .试猜想四边形
.试猜想四边形![]() 的形状,并说明理由;
的形状,并说明理由;
【实践探究】
(2)小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形![]() 中,E是边
中,E是边![]() 上一点,
上一点,![]() 于点F,
于点F,![]() 于点H,
于点H,![]() 交
交![]() 于点G,可以用等式表示线段
于点G,可以用等式表示线段![]() ,
,![]() ,
,![]() 的数量关系,请你思考并解答这个问题;
的数量关系,请你思考并解答这个问题;
【拓展迁移】
(3)小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图3,在正方形![]() 中,E是边
中,E是边![]() 上一点,
上一点,![]() 于点H,点M在
于点H,点M在![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() ,可以用等式表示线段
,可以用等式表示线段![]() ,
,![]() 的数量关系,请你思考并解答这个问题.
的数量关系,请你思考并解答这个问题.
参考答案
一、选择题(本大题共12小题,每小题3分,共36分)
【1题答案】
【答案】C
【2题答案】
【答案】B
【3题答案】
【答案】D
【4题答案】
【答案】A
【5题答案】
【答案】A
【6题答案】
【答案】B
【7题答案】
【答案】C
【8题答案】
【答案】A
【9题答案】
【答案】D
【10题答案】
【答案】A
【11题答案】
【答案】D
【12题答案】
【答案】C
二、填空题(本大题共4小题,每小题3分,共12分)
【13题答案】
【答案】![]()
【14题答案】
【答案】![]()
【15题答案】
【答案】![]()
【16题答案】
【答案】①③
三、解答题(本大题共12小题,共72分)
【17题答案】
【答案】![]()
【18题答案】
【答案】![]()
【19题答案】
【答案】![]()
【20题答案】
【答案】(1)反比例函数的表达式为![]() ;一次函数的表达式为
;一次函数的表达式为![]() ;
;
(2)![]() .
.
【21题答案】
【答案】(1)![]() ;(2)证明见解析;(3)作图见解析;
;(2)证明见解析;(3)作图见解析;
【22题答案】
【答案】“龙”字雕塑![]() 的高度为
的高度为![]() .
.
【23题答案】
【答案】(1)y关于x的函数表达式为![]() ;
;
(2)运动员从起跳点到入水点的水平距离![]() 的长为
的长为![]() .
.
【24题答案】
【答案】(1)四边形![]() 是菱形,理由见解析
是菱形,理由见解析
(2)![]() .
.
【25题答案】
【答案】(1)![]()
(2)②③ (3)![]() 人
人
【26题答案】
【答案】(1)见解析 (2)![]() 是等腰三角形,理由见解析
是等腰三角形,理由见解析
(3)![]()
【27题答案】
【答案】(1)![]()
(2)![]()
(3)![]()
【28题答案】
【答案】(1)四边形![]() 是正方形,证明见解析;(2)
是正方形,证明见解析;(2)![]() ;(3)
;(3)![]() ,证明见解析;
,证明见解析;
