2023年山东菏泽中考数学试卷及答案
一、选择题（本大题共8个小题，每小题3分，共24分，在每小题给出的四个选项中，只有一个选项是正确的，请把正确选项的序号涂在答题卡的相应位置．）
1. 剪纸文化是我国最古老的民间艺术之一，下列剪纸图案中既是轴对称图形又是中心对称图形的是（ ）
A. 
B. 
C. 
D. 
【答案】A
2. 下列运算正确的是（ ）
A. 
B. 
C. 
D. 
【答案】B
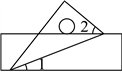
3. 一把直尺和一个含
角的直角三角板按如图方式放置，若
，则
（ ）
A. B. 
C. 
D. 
【答案】B
4. 实数a，b，c在数轴上对应点的位置如图所示，下列式子正确的是（ ）
A. 
B. 
C. 
D. 
【答案】C
5. 如图所示的几何体是由5个大小相同的小正方体组成的，它的主视图是（ ）
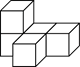
A.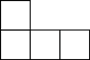 
B. 
C. 
D. 
【答案】A
6. 一元二次方程
的两根为
，则
的值为（ ）
A. 
B. 
C. 3 D. 
【答案】C
7. 
的三边长a，b，c满足
，则是（ ）
A. 等腰三角形 B. 直角三角形 C. 锐角三角形 D. 等腰直角三角形
【答案】D
8. 若一个点的纵坐标是横坐标的3倍，则称这个点为“三倍点”，如：
等都是三倍点”，在
的范围内，若二次函数
的图象上至少存在一个“三倍点”，则c的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】D
二、填空题（本大题共6个小题，每小题3分，共18分，只要求把最后结果填写在答题卡的相应区域内．）
9. 因式分解：
______．
【答案】
10. 计算：
___________．
【答案】1
11. 用数字0，1，2，3组成个位数字与十位数字不同的两位数，其中是偶数的概率为__________
【答案】
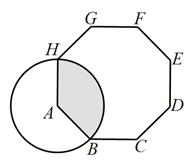
12. 如图，正八边形
的边长为4，以顶点A为圆心，
的长为半径画圆，则阴影部分的面积为__________（结果保留
）．
【答案】
13. 如图，点E是正方形
内的一点，将
绕点B按顺时针方向旋转
得到
．若
，则
__________度．
【答案】80
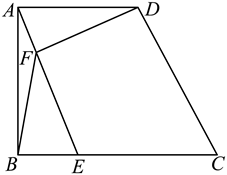
14. 如图，在四边形中，
，点E在线段
上运动，点F在线段
上，
，则线段
的最小值为__________．
【答案】
##
三、解答题（本题共78分，把解答或证明过程写在答题卡的相应区域内．）
15. 解不等式组：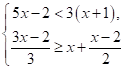
．
【答案】
16. 先化简，再求值：
，其中x，y满足
．
【答案】
，6
17. 如图，在
中，平分
，交于点E；
平分
，交
于点F．求证：
．
【答案】证明见解析
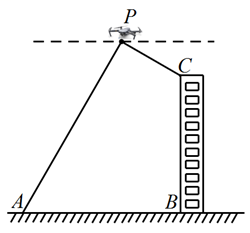
18. 无人机在实际生活中的应用广泛，如图所示，某人利用无人机测最大楼的高度，无人机在空中点P处，测得点P距地面上A点80米，点A处俯角为
，楼顶C点处的俯角为
，已知点A与大楼的距离为70米（点A，B，C，P在同一平面内），求大楼的高度（结果保留根号）
【答案】大楼的高度为
．
19. 某班学生以跨学科主题学习为载体，综合运用体育，数学，生物学等知识，研究体育课的运动负荷，在体育课基本部分运动后，测量统计了部分学生的心率情况，按心率次数x（次/分钟）分为如下五组：A组：
，B组：
，C组：
，D组：
，E组：
．其中，A组数据为73，65，74，68，74，70，66，56．根据统计数据绘制了不完整的统计图（如图所示），请结合统计图解答下列问题：
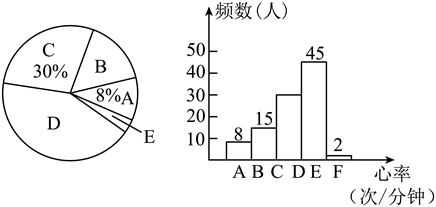
（1）A组数据的中位数是_______，众数是_______；在统计图中B组所对应的扇形圆心角是_______度；
（2）补全学生心率频数分布直方图；
（3）一般运动的适宜行为为
（次/分钟），学校共有2300名学生，请你依据此次跨学科项目研究结果，估计大约有多少名学生达到适宜心率？
【答案】（1）69，74，54；
（2）见解析 （3）大约有1725名学生达到适宜心率．
20. 如图，已知坐标轴上两点
，连接
，过点B作
，交反比例函数
在第一象限的图象于点
．
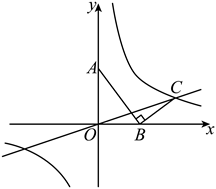
（1）求反比例函数和直线
的表达式；
（2）将直线向上平移
个单位，得到直线l，求直线l与反比例函数图象的交点坐标．
【答案】（1）
，
（2）
或
21. 某学校为美化学校环境，打造绿色校园，决定用篱笆围成一个一面靠墙（墙足够长）的矩形花园，用一道篱笆把花园分为A，B两块（如图所示），花园里种满牡丹和芍药，学校已定购篱笆120米．
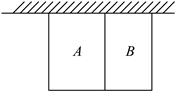
（1）设计一个使花园面积最大的方案，并求出其最大面积；
（2）在花园面积最大的条件下，A，B两块内分别种植牡丹和芍药，每平方米种植2株，知牡丹每株售价25元，芍药每株售价15元，学校计划购买费用不超过5万元，求最多可以购买多少株牡丹？
【答案】（1）长为60米，宽为20米时，有最大面积，且最大面积为1200平方米
（2）最多可以购买1400株牡丹
22. 如图，为
的直径，C是圆上一点，D是
的中点，弦
，垂足为点F．
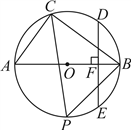
（1）求证：
；
（2）P是
上一点，
，求
；
（3）在（2）的条件下，当
是
的平分线时，求的长．
【答案】（1）证明见解析；
（2）
（3）
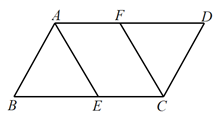
23. （1）如图1，在矩形
中，点
，
分别在边
，
上，
，垂足为点
．求证：
．
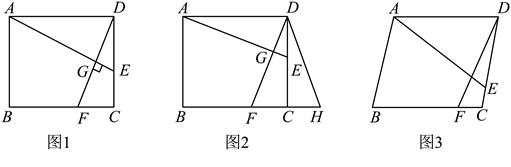
【问题解决】
（2）如图2，在正方形中，点，分别在边，上，
，延长到点
，使
，连接
．求证：
．
【类比迁移】
（3）如图3，在菱形中，点，分别在边，上，
，
，
，求
的长．
【答案】（1）见解析 （2）见解析 （3）3
24. 已知抛物线
与x轴交于A，B两点，与y轴交于点
，其对称轴为
．
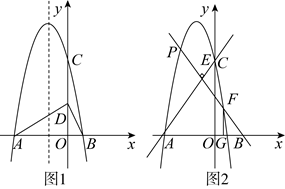
（1）求抛物线的表达式；
（2）如图1，点D是线段
上的一动点，连接
，将
沿直线
翻折，得到
，当点
恰好落在抛物线的对称轴上时，求点D的坐标；
（3）如图2，动点P在直线
上方的抛物线上，过点P作直线的垂线，分别交直线，线段于点E，F，过点F作
轴，垂足为G，求
的最大值．
【答案】（1）
（2）
（3）