2023年天津中考数学试题及答案
本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分。第Ⅰ卷为第1页至第3页,第Ⅱ卷为第4页至第8页,试卷满分120分。考试时间100分钟。
答卷前,请务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上,并在规定位置粘贴考试用条形码。答题时,务必将答案涂写在“答题卡”上,答案答在试卷上无效。考试结束后,将本试卷和“答题卡”一并交回.祝你考试顺利!
第Ⅰ卷
注意事项:
1.每题选出答案后,用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点。
2.本卷共12题,共36分。
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算![]() 的结果等于( )
的结果等于( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
2.估计![]() 的值在( )
的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
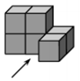
3.如图是一个由6个相同的正方体组成的立体图形,它的主视图是( )
A.![]() B.
B.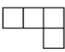 C.
C. D.
D.![]()
4.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A.全 B.面 C.发 D.展
5.据2023年5月21日《天津日报》报道,在天津举办的第七届世界智能大会通过“百网同播、万人同屏、亿人同观”,全球网友得以共享高端思想盛宴,总浏览量达到935000000人次,将数据935000000用科学记数法表示应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.![]() 的值等于( )
的值等于( )
A.1 B.![]() C.
C.![]() D.2
D.2
7.计算![]() 的结果等于( )
的结果等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若点![]() 都在反比例函数
都在反比例函数![]() 的图象上,则
的图象上,则![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.若![]() 是方程
是方程![]() 的两个根,则( )
的两个根,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,在![]() 中,分别以点A和点C为圆心,大于
中,分别以点A和点C为圆心,大于![]() 的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线
的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线![]() 分别与边
分别与边![]() 相交于点D,E,连接
相交于点D,E,连接![]() .若
.若![]() ,则
,则![]() 的长为( )
的长为( )

A.9 B.8 C.7 D.6
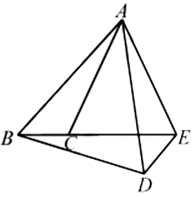
11.如图,把![]() 以点A为中心逆时针旋转得到
以点A为中心逆时针旋转得到![]() ,点B,C的对应点分别是点D,E,且点E在
,点B,C的对应点分别是点D,E,且点E在![]() 的延长线上,连接
的延长线上,连接![]() ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
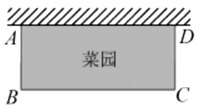
D.![]()
12.如图,要围一个矩形菜园![]() ,共中一边
,共中一边![]() 是墙,且
是墙,且![]() 的长不能超过
的长不能超过![]() ,其余的三边
,其余的三边![]() 用篱笆,且这三边的和为
用篱笆,且这三边的和为![]() .有下列结论:
.有下列结论:
①![]() 的长可以为
的长可以为![]() ;
;
②![]() 的长有两个不同的值满足菜园
的长有两个不同的值满足菜园![]() 面积为
面积为![]() ;
;
③菜园![]() 面积的最大值为
面积的最大值为![]() .
.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
第Ⅱ卷
二、填空题(本大题共6小题,每小题3分,共18分)
13.不透明袋子中装有10个球,其中有7个绿球、3个红球,这些球除颜色外无其他差别。从袋子中随机取出1个球,则它是绿球的概率为________.
14.计算![]() 的结果为________.
的结果为________.
15.计算![]() 的结果为________.
的结果为________.
16.若直线![]() 向上平移3个单位长度后经过点
向上平移3个单位长度后经过点![]() ,则m的值为________.
,则m的值为________.
17.如图,在边长为3的正方形![]() 的外侧,作等腰三角形
的外侧,作等腰三角形![]() ,
,![]() .
.

(Ⅰ)![]() 的面积为________;
的面积为________;
(Ⅱ)若F为![]() 的中点,连接
的中点,连接![]() 并延长,与
并延长,与![]() 相交于点G,则
相交于点G,则![]() 的长为________.
的长为________.
18.如图,在每个小正方形的边长为1的网格中,等边三角形![]() 内接于圆,且顶点A,B均在格点上.
内接于圆,且顶点A,B均在格点上.
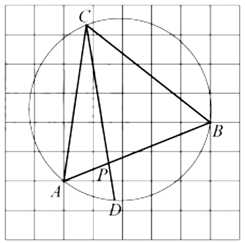
(Ⅰ)线段![]() 的长为________;
的长为________;
(Ⅱ)若点D在圆上,![]() 与
与![]() 相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使
相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使![]() 为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明)________.
为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明)________.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
19.(本小题8分)
解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得________________;
(Ⅱ)解不等式②,得________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为________________.
20.(本小题8分)
为培养青少年的劳动意识,某校开展了剪纸、编织、烘焙等丰富多彩的活动,该校为了解参加活动的学生的年龄情况,随机调查了a名参加活动的学生的年龄(单位:岁).根据统计的结果,绘制出如下的统计图①和图②.

请根据相关信息,解答下列问题:
(Ⅰ)填空:a的值为________,图①中m的值为________;
(Ⅱ)求统计的这组学生年龄数据的平均数、众数和中位数.
21.(本小题10分)
在![]() 中,半径
中,半径![]() 垂直于弦
垂直于弦![]() ,垂足为D,
,垂足为D,![]() ,E为弦
,E为弦![]() 所对的优弧上一点.
所对的优弧上一点.


(Ⅰ)如图①,求![]() 和
和![]() 的大小;
的大小;
(Ⅱ)如图②,![]() 与
与![]() 相交于点F,
相交于点F,![]() ,过点E作
,过点E作![]() 的切线,与
的切线,与![]() 的延长线相交于点G,若
的延长线相交于点G,若![]() ,求
,求![]() 的长.
的长.
22.(本小题10分)
综合与实践活动中,要利用测角仪测量塔的高度.
如图,塔![]() 前有一座高为
前有一座高为![]() 的观景台,已知
的观景台,已知![]() ,点E,C,A在同一条水平直线上.
,点E,C,A在同一条水平直线上.

某学习小组在观景台C处测得塔顶部B的仰角为![]() ,在观景台D处测得塔顶部B的仰角为
,在观景台D处测得塔顶部B的仰角为![]() .
.
(Ⅰ)求![]() 的长;
的长;
(Ⅱ)设塔![]() 的高度为h(单位:m).
的高度为h(单位:m).
①用含有h的式子表示线段![]() 的长(结果保留根号);
的长(结果保留根号);
②求塔![]() 的高度(
的高度(![]() 取0.5,
取0.5,![]() 取1.7,结果取整数).
取1.7,结果取整数).
23.(本小题10分)
已知学生宿舍、文具店、体育场依次在同一条直线上,文具店离宿舍![]() ,体育场离宿舍
,体育场离宿舍![]() ,张强从宿舍出发,先用了
,张强从宿舍出发,先用了![]() 匀速跑步去体育场,在体育场锻炼了
匀速跑步去体育场,在体育场锻炼了![]() ,之后匀速步行了
,之后匀速步行了![]() 到文具店买笔,在文具店停留
到文具店买笔,在文具店停留![]() 后,用了
后,用了![]() 匀速散步返回宿舍.下面图中x表示时间,y表示离宿舍的距离.图象反映了这个过程中张强离宿舍的距离与时间之间的对应关系.
匀速散步返回宿舍.下面图中x表示时间,y表示离宿舍的距离.图象反映了这个过程中张强离宿舍的距离与时间之间的对应关系.

请根据相关信息,回答下列问题:
(1)①填表:
张强离开宿舍的时间/ | 1 | 10 | 20 | 60 |
张强离宿舍的距离/ |
| 1.2 |
|
|
②填空:张强从体育场到文具店的速度为________![]() ;
;
③当![]() 时,请直接写出张强离宿舍的距离y关于时间x的函数解析式;
时,请直接写出张强离宿舍的距离y关于时间x的函数解析式;
(Ⅱ)当张强离开体育场![]() 时,同宿舍的李明也从体育场出发匀速步行直接回宿舍,如果李明的速度为
时,同宿舍的李明也从体育场出发匀速步行直接回宿舍,如果李明的速度为![]() ,那么他在回宿舍的途中遇到张强时离宿舍的距离是多少?(直接写出结果即可)
,那么他在回宿舍的途中遇到张强时离宿舍的距离是多少?(直接写出结果即可)
24.(本小题10分)
在平面直角坐标系中,O为原点,菱形![]() 的顶点
的顶点![]() ,矩形
,矩形![]() 的顶点
的顶点![]() .
.
(Ⅰ)填空:如图①,点C的坐标为________,点G的坐标为________;
(Ⅱ)将矩形![]() 沿水平方向向右平移,得到矩形
沿水平方向向右平移,得到矩形![]() ,点E,F,G,H的对应点分别为
,点E,F,G,H的对应点分别为![]() ,
,![]() ,
,![]() ,
,![]() .设
.设![]() ,矩形
,矩形![]() 与菱形
与菱形![]() 重叠部分的面积为S.
重叠部分的面积为S.
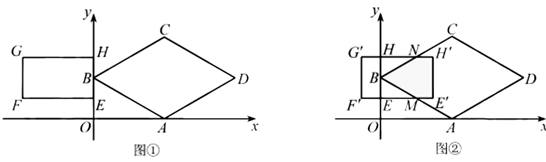
①如图②,当边![]() 与
与![]() 相交于点M、边
相交于点M、边![]() 与
与![]() 相交于点N,且矩形
相交于点N,且矩形![]() 与菱形
与菱形![]() 重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围:
重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围:
②当![]() 时,求S的取值范围(直接写出结果即可).
时,求S的取值范围(直接写出结果即可).
25.(本小题10分)
已知抛物线![]() (b,c为常数,
(b,c为常数,![]() )的顶点为P,与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,抛物线上的点M的横坐标为m,且
)的顶点为P,与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,抛物线上的点M的横坐标为m,且![]() ,过点M作
,过点M作![]() ,垂足为N.
,垂足为N.
(Ⅰ)若![]() .
.
①求点P和点A的坐标;
②当![]() 时,求点M的坐标;
时,求点M的坐标;
(Ⅱ)若点A的坐标为![]() ,且
,且![]() ,当
,当![]() 时,求点M的坐标
时,求点M的坐标
参考答案
一、选择题(本大题共12小题,每小题3分,共36分)
1.D 2.B 3.C 4.A 5.B 6.B 7.C 8.D 9.A 10.D 11.A 12.C
二、填空题(本大题共6小题,每小题3分,共18分)
13.![]() 14.
14.![]() 15.1 16.5 17.(Ⅰ)3;(Ⅱ)
15.1 16.5 17.(Ⅰ)3;(Ⅱ)![]()
18.(Ⅰ)![]() ;(Ⅱ)如图,取
;(Ⅱ)如图,取![]() 与网格线的交点E,F,连接
与网格线的交点E,F,连接![]() 并延长与网格线相交于点M,连接
并延长与网格线相交于点M,连接![]() ;连接
;连接![]() 与网格线相交于点G,连接
与网格线相交于点G,连接![]() 并延长与网格线相交于点H,连接
并延长与网格线相交于点H,连接![]() 并延长与圆相交于点I,连接
并延长与圆相交于点I,连接![]() 并延长与
并延长与![]() 的延长线相交于点Q,则点Q即为所求.
的延长线相交于点Q,则点Q即为所求.

三、解答题(本大题共7小题,共66分)
19.(本小题8分)
解:(Ⅰ)![]() ;
;
(Ⅱ)![]() ;
;
(Ⅲ)
(Ⅳ)![]() .
.
20.(本小题8分)
解:(Ⅰ)40,15.
(Ⅱ)观察条形统计图,
∵![]() ,
,
∴这组数据的平均数是14.
∵在这组数据中,15出现了16次,出现的次数最多,
∴这组数据的众数是15.
∵将这组数据按由小到大的顺序排列,处于中间的两个数都是14,有![]() ,
,
∴这组数据的中位数是14.
21.(本小题10分)
解:(Ⅰ)在![]() 中,半径
中,半径![]() 垂直于弦
垂直于弦![]() ,
,
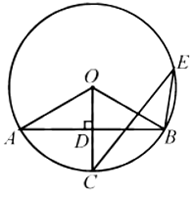
∴![]() ,得
,得![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(Ⅱ)如图,连接![]()
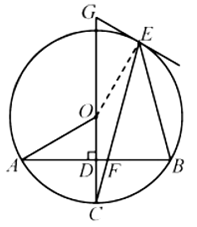
同(Ⅰ)得![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
又![]() ,
,
∴![]() .
.
∵![]() 与
与![]() 相切于点E,
相切于点E,
∴![]() ,即
,即![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
22.(本小题10分)
解:(Ⅰ)在![]() 中,
中,![]() ,
,
∴![]() .即
.即![]() 的长为
的长为![]() .
.
(Ⅱ)①在![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,由
中,由![]() ,得
,得![]() .
.
∴![]() .
.
即![]() 的长为
的长为![]() .
.
②如图,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
根据题意,![]() ,
,
∴四边形![]() 是矩形.
是矩形.
∴![]() .
.
可得![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .即
.即![]() .
.
∴![]() .
.
答:塔![]() 的高度约为
的高度约为![]() .
.
23.(本小题10分)
解:(Ⅰ)①0.12,1.2,0.6;
②0.06;
(3)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
(Ⅱ)![]() .
.
24.(本小题满分8分)
解:(Ⅰ)![]() ,
,![]() .
.
(Ⅱ)①∵点![]() ,点
,点![]() ,点
,点![]() ,
,
∴矩形![]() 中,
中,![]() 轴,
轴,![]() 轴,
轴,![]() .
.
∴矩形![]() 中,
中,![]() 轴,
轴,![]() 轴,
轴,![]() .
.
由点![]() ,点
,点![]() ,得
,得![]() .
.
在![]() 中,
中,![]() ,得
,得![]() .
.
在![]() 中,由
中,由![]() ,得
,得![]()
∴![]() .同理,得
.同理,得![]() .
.
∵![]() ,得
,得![]() .
.
又![]() ,
,
∴![]() ,其中
,其中![]() 的取值范围是
的取值范围是![]() .
.
②![]() .
.
25.(本小题10分)
解:(Ⅰ)(1)由![]() ,得抛物线的解析式为
,得抛物线的解析式为![]() .
.
∵![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,
时,![]() .解得
.解得![]() .又点
.又点![]() 在点
在点![]() 的左侧,
的左侧,
∴点![]() 的坐标为
的坐标为![]() .
.
②过点![]() 作
作![]() 轴于点
轴于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
∵点![]() ,点
,点![]() ,
,
∴![]() .可得
.可得![]() 中,
中,![]() .
.
∴![]() 中,
中,![]() .
.
∵抛物线![]() 上的点
上的点![]() 的横坐标为
的横坐标为![]() ,其中
,其中![]() ,
,
∴点![]() ,点
,点![]() .
.
得![]() .即点
.即点![]() .
.
∴![]() .
.
![]() 中,可得
中,可得![]() .
.
∴![]() .又
.又![]() ,
,
得![]() .即
.即![]() .解得
.解得![]() (舍)
(舍)
∴点![]() 的坐标为
的坐标为![]() .
.
(Ⅱ)∵点![]() 在抛物线
在抛物线![]() 上,其中
上,其中![]() ,
,
∴![]() .得
.得![]() .
.
∴扡物线的解析式为![]() .
.
得点![]() ,其中
,其中![]() .
.
∵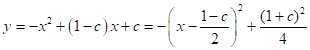 ,
,
∴顶点![]() 的坐标为
的坐标为 ,对称轴为直线
,对称轴为直线![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,点
,点![]() .
.
由![]() ,得
,得![]() .于是
.于是![]() .
.
∴![]() .
.
即![]() .解得
.解得![]() (舍).
(舍).
同(Ⅰ),过点![]() 作
作![]() 轴于点
轴于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,
,
则点![]() ,点
,点![]() ,点
,点![]() .
.
∵![]() ,
,
∴![]() .
.
即![]() .解得
.解得![]() (舍).
(舍).
∴点![]() 的坐标为
的坐标为![]()
