2022年重庆中考数学试题卷及答案(B卷)
(全卷共四个大题,满分150分,考试时间120分钟)
注意事项:
1.试题的答案书写在答题卡上,不得在试题卷上直接作答;
2.作答前认真阅读答题卡的注意事项;
3.作图(包括作辅助线)请一律用黑色2B铅笔完成;
参考公式:抛物线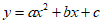 (
(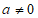 )的顶点坐标为
)的顶点坐标为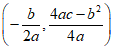 ,对称轴为
,对称轴为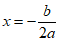 .
.
一、选择题(共12个小题,每小题4分,共48分)在每个小题的下面,都给出了序号为A、B、C、D的四个选项,其中只有一个正确的,请将答题卡上题号右侧的正确答案所对应的方框涂黑.
1.2的相反数是( )
A.-2 B.2 C.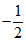 D.
D.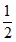
2.下列北京冬奥会运动标识图案是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
3.如图,直线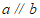 ,直线m与a,b相交,若
,直线m与a,b相交,若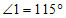 ,则
,则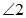 的度数为( )
的度数为( )
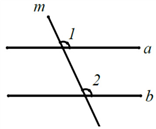
A.115° B.105° C.75° D.65°
4.如图是小颖0到12时的心跳速度变化图,在这一时段内心跳速度最快的时刻约为( )
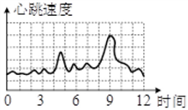
A.3时 B.6时 C.9时 D.12时
5.如图,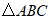 与
与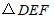 位似,点O是它们的位似中心,且相似比为1∶2,则
位似,点O是它们的位似中心,且相似比为1∶2,则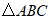 与
与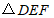 的周长之比是( )
的周长之比是( )
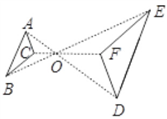
A.1∶2 B.1∶4 C.1∶3 D.1∶9
6.把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为( )
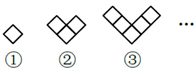
A.15 B.13 C.11 D.9
7.估计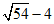 的值在( )
的值在( )
A.6到7之间 B.5到6之间 C.4到5之间 D.3到4之间
8.学校连续三年组织学生参加义务植树,第一年共植树400棵,第三年共植树625棵.设该校植树棵数的年平均增长率为x,根据题意,下列方程正确的是( )
A.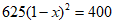 B.
B.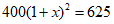 C.
C.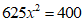 D.
D.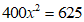
9.如图,在正方形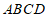 中,对角线
中,对角线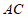 、
、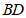 相交于点O. E、F分别为
相交于点O. E、F分别为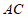 、
、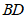 上一点,且
上一点,且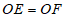 ,连接
,连接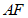 ,
,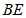 ,
,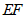 .若
.若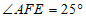 ,则
,则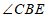 的度数为( )
的度数为( )
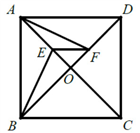
A.50° B.55° C.65° D.70°
10.如图,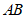 是
是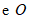 的直径,C为
的直径,C为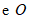 上一点,过点C的切线与
上一点,过点C的切线与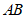 的延长线交于点P,若
的延长线交于点P,若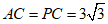 ,则
,则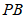 的长为( )
的长为( )
A.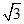 B.
B.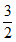 C.
C.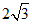 D.3
D.3
11.关于x的分式方程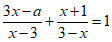 的解为正数,且关于y的不等式组
的解为正数,且关于y的不等式组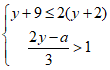 的解集为
的解集为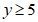 ,则所有满足条件的整数a的值之和是( )
,则所有满足条件的整数a的值之和是( )
A.13 B.15 C.18 D.20
12.对多项式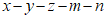 任意加括号后仍然只含减法运算并将所得式子化简,称之为“加算操作”,例如:
任意加括号后仍然只含减法运算并将所得式子化简,称之为“加算操作”,例如: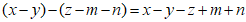 ,
,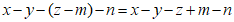 ,…,给出下列说法:
,…,给出下列说法:
①至少存在一种“加算操作”,使其结果与原多项式相等;
②不存在任何“加算操作”,使其结果与原多项式之和为0;
③所有的“加算操作”共有8种不同的结果.以上说法中正确的个数为( )
A.0 B.1 C.2 D.3
二、填空题(共4个小题,每小题4分,共16分)请将每小题的答案直接填在答题卡中对应的横线上.
13.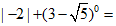 _________.
_________.
14.在不透明的口袋中装有2个红球,1个白球,它们除颜色外无其他差别,从口袋中随机摸出一个球后,放回并摇匀,再随机摸出一个球,两次摸出的球都是红球的概率为_________.
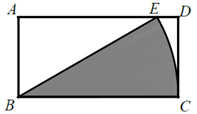
15.如图,在矩形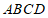 中,
中,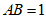 ,
,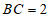 ,以B为圆心,
,以B为圆心,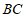 的长为半轻画弧,交
的长为半轻画弧,交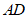 于点E.则图中阴影部分的面积为_________.(结果保留
于点E.则图中阴影部分的面积为_________.(结果保留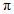 )
)
16.特产专卖店销售桃片、米花糖、麻花三种特产,其中每包桃片的成本是麻花的2倍,每包桃片、米花糖、麻花的售价分别比其成本高20%、30%、20%.该店五月份销售桃片、米花糖、麻花的数量之比为1∶3∶2,三种特产的总利润是总成本的25%,则每包米花糖与每包麻花的成本之比为_________.
三、解答题(共2个小题,每小题8分,共16分)
17.计算:(1)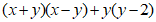 ; (2)
; (2)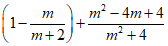 .
.
18.我们知道,矩形的面积等于这个矩形的长乘宽,小明想用其验证一个底为a,高为h的三角形的面积公式为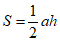 .想法是:以
.想法是:以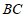 为边作矩形
为边作矩形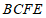 ,点A在边
,点A在边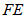 上,再过点A作
上,再过点A作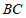 的垂线,将其转化为证三角形全等,由全等图形面积相等来得到验证.按以上思路完成下面的作图与填空:证明:用直尺和圆规过点A作
的垂线,将其转化为证三角形全等,由全等图形面积相等来得到验证.按以上思路完成下面的作图与填空:证明:用直尺和圆规过点A作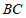 的垂线
的垂线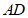 交
交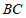 于点D.(只保留作图痕迹)
于点D.(只保留作图痕迹)
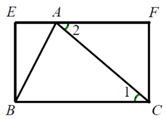
在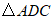 和
和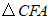 中,
中,
∵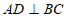 ,
,
∴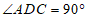 .
.
∵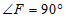 ,
,
∴______①____.
∵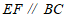 ,
,
∴______②_____.
又∵____③______.
∴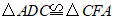 (
(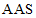 ).
).
同理可得:_____④______.
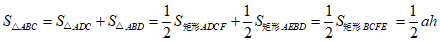 .
.
三、解答题(共7个小题,每小题10分,共70分)
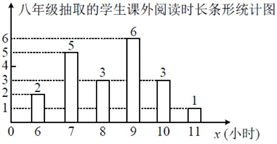
19.在“世界读书日”到来之际,学校开展了课外阅读主题周活动,活动结束后,经初步统计,所有学生的课外阅读时长都不低于6小时,但不足12小时,从七,八年级中各随机抽取了20名学生,对他们在活动期间课外阅读时长(单位:小时)进行整理、描述和分析(阅读时长记为x,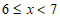 ,记为6;
,记为6;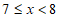 ,记为7;
,记为7;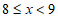 ,记为8;…以此类推),下面分别给出了抽取的学生课外阅读时长的部分信息,
,记为8;…以此类推),下面分别给出了抽取的学生课外阅读时长的部分信息,
七年级抽取的学生课外阅读时长:
6,7,7,7,7,8,8,8,8,8,8,8,9,9,9,9,9,10,10,11,
| ||
七、八年级抽取的学生课外阅读时长统计表 | ||
年级 | 七年级 | 八年级 |
平均数 | 8.3 | 8.3 |
众数 | a | 9 |
中位数 | 8 | b |
8小时及以上所占百分比 | 75% | c |
根据以上信息,解答下列问题:
(1)填空: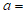 ______________,
______________,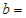 ______________,
______________,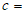 ______________.
______________.
(2)该校七年级有400名学生,估计七年级在主题周活动期间课外阅读时长在9小时及以上的学生人数.
(3)根据以上数据,你认为该校七,八年级学生在主题周活动中,哪个年级学生的阅读积极性更高?请说明理由,(写出一条理由即可)
20.反比例函数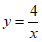 的图象如图所示,一次函数
的图象如图所示,一次函数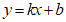 (
(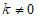 )的图象与
)的图象与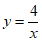 的图象交于
的图象交于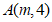 ,
,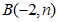 两点,
两点,

(1)求一次函数的表达式,并在所给的平面直角坐标系中面出该函数的图象;
(2)观察图象,直接写出不等式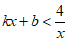 的解集;
的解集;
(3)一次函数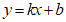 的图象与x轴交于点C,连接
的图象与x轴交于点C,连接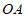 ,求
,求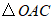 的面积.
的面积.
21.为保障蔬菜基地种植用水,需要修建灌溉水渠.
(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工人员,每天比原来多修建20米,再施工2天完成任务,求甲施工队增加人员后每天修建灌溉水渠多少米?
(2)因基地面积扩大,现还需修建另一条灌溉水渠1800米,为早日完成任务,决定派乙施工队与甲施工队同时开工合作修建这条水渠,直至完工.甲施工队按(1)中增加人员后的修建速度进行施工.乙施工队修建360米后,通过技术更新,每天比原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好相同.求乙施工队原来每天修建灌溉水渠多少米?
22.湖中小岛上码头C处一名游客突发疾病,需要救援.位于湖面B点处的快艇和湖岸A处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头C接该游客,再沿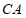 方向行驶,与救援船相遇后将该游客转运到救援船上.已知C在A的北偏东30°方向上,B在A的北偏东60°方向上,且在C的正南方向900米处.
方向行驶,与救援船相遇后将该游客转运到救援船上.已知C在A的北偏东30°方向上,B在A的北偏东60°方向上,且在C的正南方向900米处.

(1)求湖岸A与码头C的距离(结果精确到1米,参考数据: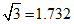 );
);
(2)救援船的平均速度为150米/分,快艇的平均速度为400米/分,在接到通知后,快艇能否在5分钟内将该游客送上救援船?请说明理由.(接送游客上下船的时间忽略不计)
23.对于一个各数位上的数字均不为0的三位自然数N,若N能被它的各数位上的数字之和m整除,则称N是m的“和倍数”.
例如:∵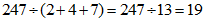 ,∴247是13的“和倍数”.
,∴247是13的“和倍数”.
又如:∵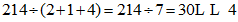 ,∴214不是“和倍数”.
,∴214不是“和倍数”.
(1)判断357,441是否是“和倍数”?说明理由;
(2)三位数A是12的“和倍数”,a,b,c分别是数A其中一个数位上的数字,且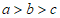 .在a,b,c中任选两个组成两位数,其中最大的两位数记为
.在a,b,c中任选两个组成两位数,其中最大的两位数记为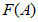 ,最小的两位数记为
,最小的两位数记为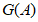 ,若
,若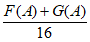 为整数,求出满足条件的所有数A.
为整数,求出满足条件的所有数A.
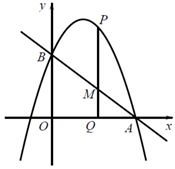
24.如图,在平面直角坐标系中,抛物线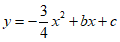 与x轴交于点
与x轴交于点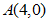 ,与y轴交于点
,与y轴交于点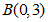 .
.
(1)求抛物线的函数表达式;
(2)点P为直线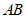 上方抛物线上一动点,过点P作
上方抛物线上一动点,过点P作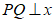 轴于点Q,交
轴于点Q,交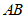 于点M,求
于点M,求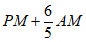 的最大值及此时点P的坐标;
的最大值及此时点P的坐标;
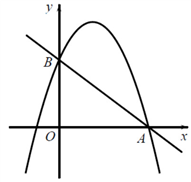
(3)在(2)的条件下,点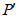 与点P关于抛物线
与点P关于抛物线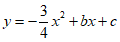 的对称轴对称.将抛物线
的对称轴对称.将抛物线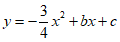 向右平移,使新抛物线的对称轴l经过点A.点C在新抛物线上,点D在l上,直接写出所有使得以点A、
向右平移,使新抛物线的对称轴l经过点A.点C在新抛物线上,点D在l上,直接写出所有使得以点A、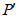 、C、D为顶点的四边形是平行四边形的点D的坐标,并把求其中一个点D的坐标的过程写出来.
、C、D为顶点的四边形是平行四边形的点D的坐标,并把求其中一个点D的坐标的过程写出来.
25.在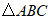 中,
中,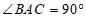 ,
,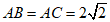 ,D为
,D为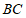 的中点,E,F分别为
的中点,E,F分别为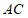 ,
,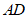 上任意一点,连接
上任意一点,连接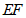 ,将线段
,将线段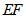 绕点E顺时针旋转90°得到线段
绕点E顺时针旋转90°得到线段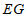 ,连接
,连接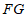 ,
,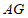 .
.
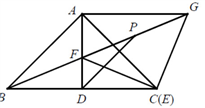
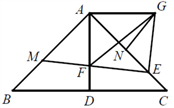
(1)如图1,点E与点C重合,且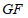 的延长线过点B,若点P为
的延长线过点B,若点P为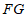 的中点,连接
的中点,连接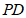 ,求
,求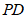 的长;
的长;
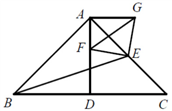
(2)如图2,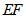 的延长线交
的延长线交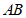 于点M,点N在
于点M,点N在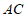 上,
上,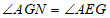 且
且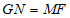 ,求证:
,求证: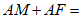
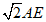 ;
;
(3)如图3,F为线段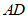 上一动点,E为
上一动点,E为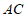 的中点,连接
的中点,连接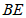 ,H为直线
,H为直线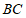 上一动点,连接
上一动点,连接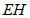 ,将
,将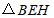 沿
沿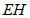 翻折至
翻折至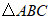 所在平面内,得到
所在平面内,得到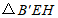 ,连接
,连接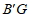 ,直接写出线段
,直接写出线段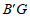 的长度的最小值.
的长度的最小值.